1.4 练习

104. 二叉树的最大深度

int maxDepth(struct TreeNode *root, int len) 
{
	if (root == NULL) {
		return len;
	}

	return fmax(maxDepth(root->left, len+1), maxDepth(root->right, len+1));
}

二叉树最大深度就是基本的递归思路的求解， 手法主要是递归下去之后len改如何赋值有点搞不清，这里给出了demo的用例，只要能递归就加+1，最后递归到叶子节点返回len。
手法：利用 “递”

111. 二叉树的最小深度

手法：利用 “归” ，这里不同于二叉树的深度求解，深度是利用递的性质，本题是先递下去，再归时做了处理。（具体见下面代码注释部分）

int minDepth(struct TreeNode *root) {
	if (root == NULL) {
		return 0;
	}

	if (root->left == NULL && root->right == NULL) {
		return 1;
	}

	int min_depth = INT_MAX; // 手法2：归上来时，要保证每次函数返回值与min_depth的fmin操作时
							//  函数返回值都能保留下来，所以min_depth要设置最大值.
	if (root->left != NULL) {
		min_depth = fmin(minDepth(root->left), min_depth);
	}
	if (root->right != NULL) {
		min_depth = fmin(minDepth(root->right), min_depth);
	}

	return min_depth + 1; // 手法1：利用归的特性，先递下去求解到叶子节点的数值，进入到循环终止条件
	                      // 然后每层，逐层归上来时+1.
}

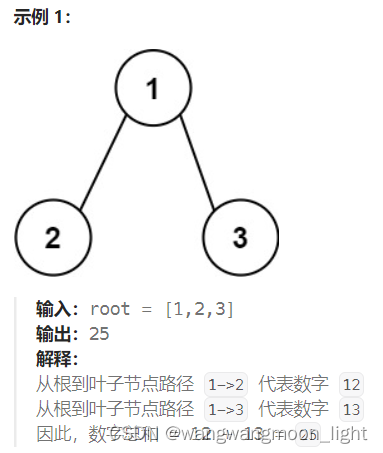
049. 求从根节点到叶节点的路径数字之和

int dfs(struct TreeNode *root, int prevSum) {
    if (root == NULL) {
        return 0;
    }
    int sum = prevSum * 10 + root->val;
    if (root->left == NULL && root->right == NULL) {
        return sum; // 递归终止条件
    } else {
        return dfs(root->left, sum) + dfs(root->right, sum);
        // 先递归下去左叶子节点，计算出来，然后递归右叶子节点
    }
}

int sumNumbers(struct TreeNode *root) {
    return dfs(root, 0);
}

93. 复原 IP 地址

#define MAX 166     // 排列组合简单算的，实际没有这么多，很多情况不合法
void dfs(char *s, char **res, int *returnSize, int step, int index, int len, char *temp) 
{
	if (step == 4) {    // 结束条件：已取完四个数，将结果添加至结果数组
		res[*returnSize] = (char*)malloc(sizeof(char)*(len + 4));
		temp[index + step - 1] = '\0';      //将最后一个'.'去掉
		strcpy(res[*returnSize], temp);
		(*returnSize)++;
		return;
	}
	// 取一位数；
	// 剪枝：剩余长度不合法的情况
	// 剩余长度属于 [(3 - step)， (3 - step) * 3]
	if ((len - index - 1 <= (3 - step) * 3) && (len - index - 1 >= (3 - step))) {
		temp[index + step]     = s[index];
		temp[index + step + 1] = '.';
		dfs(s, res, returnSize, step + 1, index + 1, len, temp);
	}
	// 取两位合法数（首位不为0）； s[index] != '0'
	// 剪枝：剩余长度不合法的情况
	if ((len - index - 2 <= (3 - step) * 3) && ((len - index - 2 >= (3 - step)) && (s[index] != '0'))) {
		temp[index + step]     = s[index];
		temp[index + step + 1] = s[index + 1];
		temp[index + step + 2] = '.';
		dfs(s, res, returnSize, step + 1, index + 2, len, temp);
	}
	// 取三位合法数（首位不为0，且<=255）；
	// 剪枝：剩余长度不合法的情况
	if ((len - index - 3 <= (3 - step) * 3) && (len - index - 3 >= (3 - step)) && ((s[index] != '0') && ((s[index] - '0') * 100 + (s[index + 1] - '0') * 10 + s[index + 2] - '0' <= 255))) {
		temp[index + step]     = s[index];
		temp[index + step + 1] = s[index + 1];
		temp[index + step + 2] = s[index + 2];
		temp[index + step + 3] = '.';
		dfs(s, res, returnSize, step + 1, index + 3, len, temp);
	}
}

char **restoreIpAddresses(char *s, int *returnSize) 
{
	*returnSize = 0;
	int len = strlen(s);
	if (len > 12 || len < 4) {
		return NULL;     //长度不合法直接return
	}
	char **res = (char **)malloc(sizeof(char *) * MAX);
	char *temp = (char *)malloc(sizeof(char) * (len + 5));
	dfs(s, res, returnSize, 0, 0, len, temp);
	return res;
}

130. 被围绕的区域

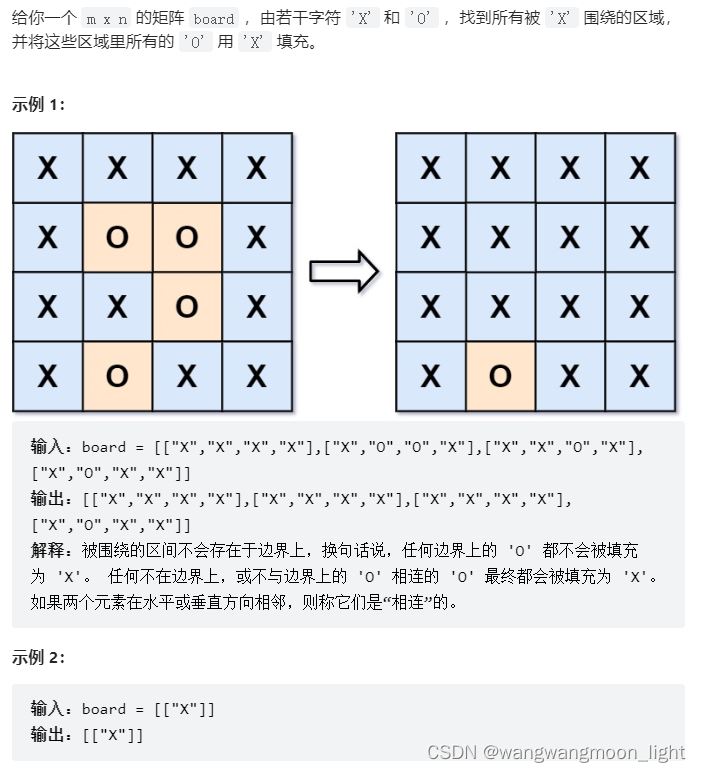
注意到题目解释中提到：任何边界上的 O 都不会被填充为 X。 我们可以想到，所有的不被包围的 O 都直接或间接与边界上的 O 相连。我们可以利用这个性质判断 O 是否在边界上，具体地说：

对于每一个边界上的 O，我们以它为起点，标记所有与它直接或间接相连的字母 O；
最后我们遍历这个矩阵，对于每一个字母：
如果该字母被标记过，则该字母为没有被字母 X 包围的字母 O，我们将其还原为字母 O；
如果该字母没有被标记过，则该字母为被字母 X 包围的字母 O，我们将其修改为字母 X

void dfs(char **board, int x, int y, int row, int col)
{
	if (x < 0 || x >= row || y < 0 || y >= col || board[x][y] != 'O') {  // 从边界的'O'出发遍历与之直接或间接相邻的'O'
		return;
	}

	board[x][y] = 'Z';  // 暂时将与边界上的'O'直接或间接相邻的'O'标记为'Z'
	dfs(board, x + 1, y, row, col);  // 向下遍历
	dfs(board, x - 1, y, row, col);  // 向上遍历
	dfs(board, x, y + 1, row, col);  // 向右遍历
	dfs(board, x, y - 1, row, col);  // 向左遍历
}

void solve(char **board, int boardSize, int *boardColSize)
{
	if (board == NULL || boardSize == 0 || (*boardColSize) == 0) {
		return;
	}
	int row = boardSize;
	int col = (*boardColSize);
	int i, j;

	for (i = 0; i < col; i++) {  
		// 寻找与第一行的'O'直接或间接相邻的'O'
		if (board[0][i] == 'O') {
			dfs(board, 0, i, row, col);
		}
		// 寻找与最后一行的'O'直接或间接相邻的'O'
		if (board[row - 1][i] == 'O') {
			dfs(board, row - 1, i, row, col);
		}
	}

	for (i = 0; i < row; i++) {  
		// 寻找与第一列的'O'直接或间接相邻的'O'
		if (board[i][0] == 'O') {
			dfs(board, i, 0, row, col);
		}
		// 寻找与最后一列的'O'直接或间接相邻的'O'
		if (board[i][col - 1] == 'O') {
			dfs(board, i, col - 1, row, col);
		}
	}

	// 结果
	for (i = 0; i < row; i++) {  // 将被'X'围绕的'O'转换为'X'
		for (j = 0; j < col; j++) {
			if (board[i][j] == 'O') {
				board[i][j] = 'X';
			}
			else if (board[i][j] == 'Z') { // 之前将不被'X'围绕的'O'转换为'Z'，现在恢复为'O'
				board[i][j] = 'O';
			}
		}
	}
}

22. 括号生成

// 回溯法求解
#define MAX_SIZE 1430  // 卡特兰数: 1, 1, 2, 5, 14, 42, 132, 429, 1430
void generate(int left, int right, int n, char *str, int index, char **result, int *returnSize) 
{
	if (index == 2 * n) { // 当前长度已达2n
		result[(*returnSize)] = (char *)malloc((2 * n + 1) * sizeof(char));
		memset(result[(*returnSize)], 0, (2 * n + 1) * sizeof(char));
		strcpy(result[(*returnSize)++], str);
		return;
	}
	// 如果左括号数量不大于 n，可以放一个左括号
	if (left < n) {
		str[index] = '(';
		generate(left + 1, right, n, str, index + 1, result, returnSize);
	}
	// 如果右括号数量小于左括号的数量，可以放一个右括号
	if (right < left) {
		str[index] = ')';
		generate(left, right + 1, n, str, index + 1, result, returnSize);
	}
}
/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
char **generateParenthesis(int n, int *returnSize)
{
	char *str = (char *)malloc((2 * n + 1) * sizeof(char));
	memset(str, 0 ,(2 * n + 1) * sizeof(char));
	char **result = (char **)malloc(sizeof(char *) * MAX_SIZE);
	*returnSize = 0;
	generate(0, 0, n, str, 0, result, returnSize);
	return result;
}