计算机组成原理【CO】Ch2 数据的表示和应用

文章目录

大纲
- 2.1 数制与编码
- 2.2 运算方法和运算电路
- 2.3 浮点数的表示和运算
【※】带标志加法器
- OF
- SF
- ZF
- CF
- 计算机怎么区分有符号数无符号数?
【※】存储排列和数据类型转换
- 数据类型大小
- 数据类型转换
进位计数制
- 进制转换
- 2的次幂
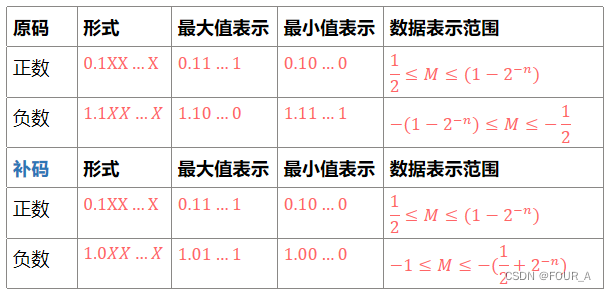
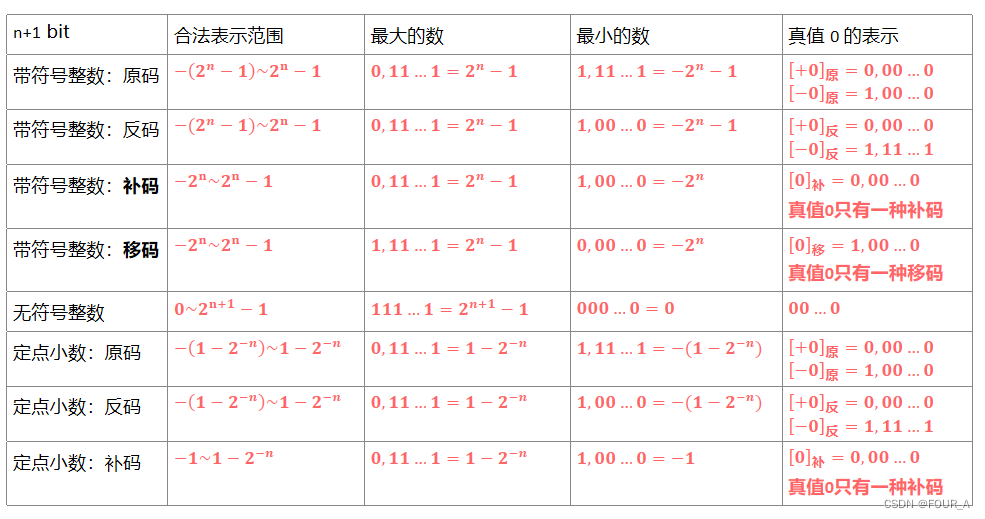
各种码的基本特性
无符号整数的表示和运算
带符号整数的表示和运算
码之间的转换
移位运算
- 算数移位【针对有符号数】
- 逻辑移位【针对无符号数】
- 循环移位
乘除运算
- 无符号整数
- 有符号数
【※】IEEE754
- IEEE754浮点数与真值相互转化
- - 由浮点数确定真值(阶码不是全0、也不是全1) :
- 浮点数的加减运算
C强制类型转换
浮点数的规格化

大纲

2.1 数制与编码

王道书和大学教材讲到原码、补码时，使用了数学化的语言来讲解，不用过于深究，不是重点。计组这门课在考试中只考察应用，不考数学原理。对补码的数学原理感兴趣的同学，可以研究《数论》。
这个小节学起来难，但做起题来不算难。不建议反复死磕视频和王道书，可以先学一遍，然后直接做题，用“做题驱动复习”。

2.2 运算方法和运算电路

本节内容较多，一天的时间可能学不完。建议大家按照“伴学营打卡表”推荐的顺序做题，学一部分，做几道题。不建议一口气全部看完再去做题，那样一定消化不了。
对于没学过《数字电路》的同学，串行加法器、并行加法器的底层原理一定很难理解。不过没关系，考试不可能考太底层的电路设计。
带标志位的加法器是考试重点，也是经常结合第四章考察的重点，需要认真理解。OF、SF、ZF、CF 标志位的生成和作用一定要掌握。
乘法、除法的原理细节不容易理解，但考察频率较低，第一次学如果觉得难，也不建议花太多时间。只需要先建立起这个认知：在计算机硬件层面，无论是乘法还是除法，都是通过加法、减法、移位运算来实现的。
C语言中各种数据类型的存储和相互转换、数据的存储和排列，这两部分内容很重要，经常结合大题考察，需认真理解。

2.3 浮点数的表示和运算

本节又是一块硬骨头，没什么好说的，学吧。第一次学难免让人怀疑人生，保持平常心尽力去学尽力去做题就好。第一次学习不建议死磕细节，得配合做题来体会这个部分怎么考，用“做题驱动复习”。
但很多同学的反馈是：“第一次学感觉很复杂，但第二轮回来复习感觉也没那么难”。原因是，本节内容虽难，但在经过做题训练之后，大家都会更清晰的认识到 “哪些地方是考试重点”、““哪些地方应该是我重点关注的”。

【※】带标志加法器

OF

有符号数的加减运算是否发生了溢出。
OF=1时，说明发生了溢出
OF=最高位产生的进位 ⊕ 次高位产生的进位
OF位对无符号数的加减法无意义

SF

有符号数加减运算结果的正负性。
SF=0表示运算结果为正数，SF=1表示运算结果为负数
SF = 最高位的本位和（也是结果的最高位）
SF位对无符号数的加减法无意义

ZF

表示运算结果是否为0。
ZF=1表示运算结果为0，ZF=0表示运算结果非0
两个数的运算结果为n bit，只有n bit全为0时，ZF =1
对有符号、无符号都有意义

CF

进位、借位标志
表示无符号数的加减法是否发生了进位或借位
当CF=1时，说明无符号数的加减法发生了进位或借位，即发生了溢出
CF=最高位产生的进位⊕sub
- sub=1，表示减法
- sub=0，表示加法
CF位对有符号数的加减法无意义
有符号数的加减运算是否发生了溢出。
OF=1时，说明发生了溢出
OF=最高位产生的进位 ⊕ 次高位产生的进位
OF位对无符号数的加减法无意义

计算机怎么区分有符号数无符号数?

标志位会保存在PSW，ALU无法区分有符号数和无符号数，但由于计算机分为无符号加法和有符号加法。指令不同，执行时安排的微操作不同，从而区分有符号数和无符号数。

【※】存储排列和数据类型转换

数据类型大小

char：1B
short：2B
int：4B
float：4B
long：4B
double：8B

Tips:

C语言中定点整数是用补码存储的

数据类型转换

整数之间转换（带符号和无符号之间）

长度相同
- 机器数不变，解释方式改变
短变长
- 先扩展：
  - 无符号数补0
  - 有符号数补符号
- 再解释
长变短
- 直接截断，只留下低位
- 再解释

整数与浮点数之间的转换

整数转浮点数：
- 先转换为2进制，写出科学记数法1.xxxx，再转为浮点数，截断尾部采用0舍1入的原则
- ⚠️可能精度丢失
浮点数转整数：
- 写出二进制小数，去掉小数部分，整数部分保留更低的位数
- ⚠️可能溢出、精度丢失

进位计数制

进制转换

二进制 <-> 八进制：每3个二进制位对应一个八进制位
二进制 <-> 十六进制：每4个二进制位对应一个十六进制位
- 【PS：整数部分前面补0，小数部分后面补0】
十进制 -> 进制
- 整数部分:除基取余法，先取得的“余”是整数的低位
- 小数部分:乘基取整法，先取得的“整”是小数的高位

2的次幂

次幂	2的次幂
-4	0.0625
-3	0.125
-2	0.25
-1	0.5
0	1
1	2
2	4
3	8
4	16
5	32
6	64
7	128
8	256
9	512
10	1024
11	2048
12	4096
13	8192
14	16384
15	32768
16	65536

各种码的基本特性

在这里插入图片描述

无符号整数的表示和运算

• 加法
• 全部位按位相加
• 减法
• $x - y = x + [- y]$
• $[- y$ ]是 $[y]$ 从右往左第一个1的左边全部取反
• 溢出
• 手算：判断加减法的结果是否超出无符号数合法表示范围
• 机算： $CF = 最高位进位 \oplus S u b$

带符号整数的表示和运算

Tips：
• 计算机内部，所有带符号整数的加减法都要先转换为补码

计算机硬件如何做带符号数补码的加法:
• 从最低位开始，所有位按位相加（符号位参与运算），并往更高位进位

计算机硬件如何做带符号数补码的减法:
• "被减数”不变，“减数”从右往左找到第一个1，这个1左边的全部位按位取反减法变加法

有符号数：
• 加法
• 按位相加
• 减法
• $x]_补 - [y]_补 = [x]_补 + [−y]_补$
• $y]_补是 [y]_补$ 从右往左第一个1的左边全部位按位取反
• 溢出
• 手算：判断加减法的结果是否超出有符号数合法表示范围
• 机算： $OF = 最高位进位 \oplus 次高位进位$

码之间的转换

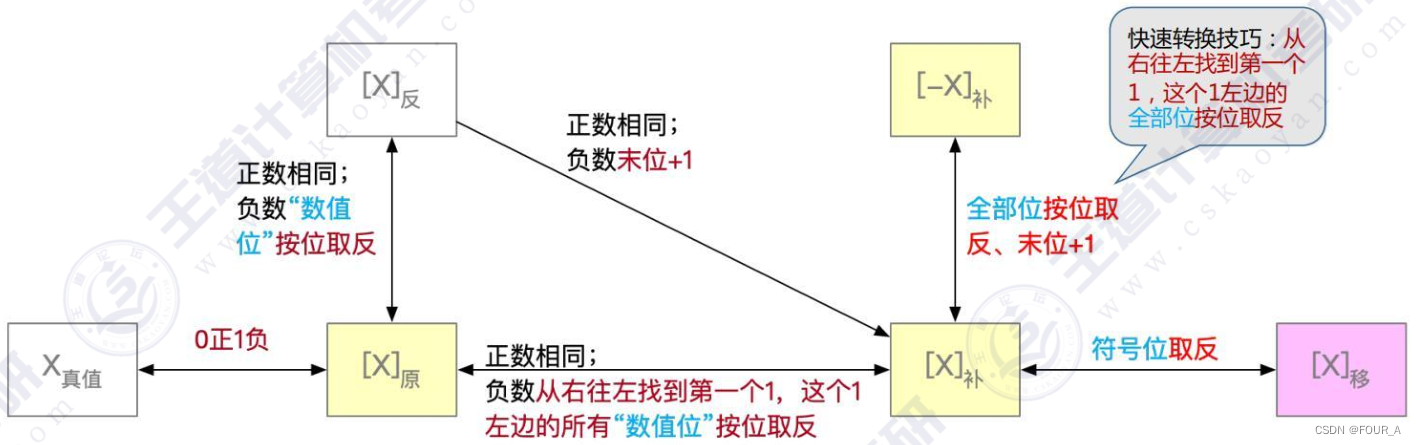
在这里插入图片描述

[x]_移→[−x]_移：全部位按位取反，末位+1
使用补码表示时，若符号位相同，则数值位越大，码值越大

$x]_原→[x]_反？$
• 正数：不变
• 负数：符号位不变，数值位按位取反
$x]_原↔[x]_补？$
• 正数：不变
• 负数：符号位不变，从右往左找到第一个“1”，这个1左边的所有“数值位”按位取反
$x]_补↔[−x]_补？$
• 从右往左找到第一个“1”，这个1左边的全部位按位取反
$x]_补↔[x]_移？$
• 符号位取反

如何用补码快速计算真值：
- 直接在补码前面加上负号，再计算值
○ Eg： $1110]_补 = −2^3 + 2^2 + 2 = −2$
- 遇到一大串的1，将其看作符号位，直接化为最简，再用上述方法
○ Eg： $11111110]_补 = [10]_补 = −2$

如何快速求真值的补码：
eg： $8190 = −8192 + 2 = [1110,0000,0000,0010]_补 = E002H$

移位运算

算数移位【针对有符号数】

左移1位相当于乘基数；右移1位相当于除基数，但由于位数有限，所以有时候算数移位并不能完全等效于乘除运算。
是针对有符号数：符号位保持不变。
- 正数：原码、反码、补码，无论左移还是右移都是补0
- 负数：
  - 原码左移、右移都补0
  - 反码左移和右移都补1
  - 补码左移补0，右移补1
若采用双符号位来表示数，则最高符号位永远是真正的符号位，因此在算术移位时只有高符号位保留不变，低符号位要参与移位