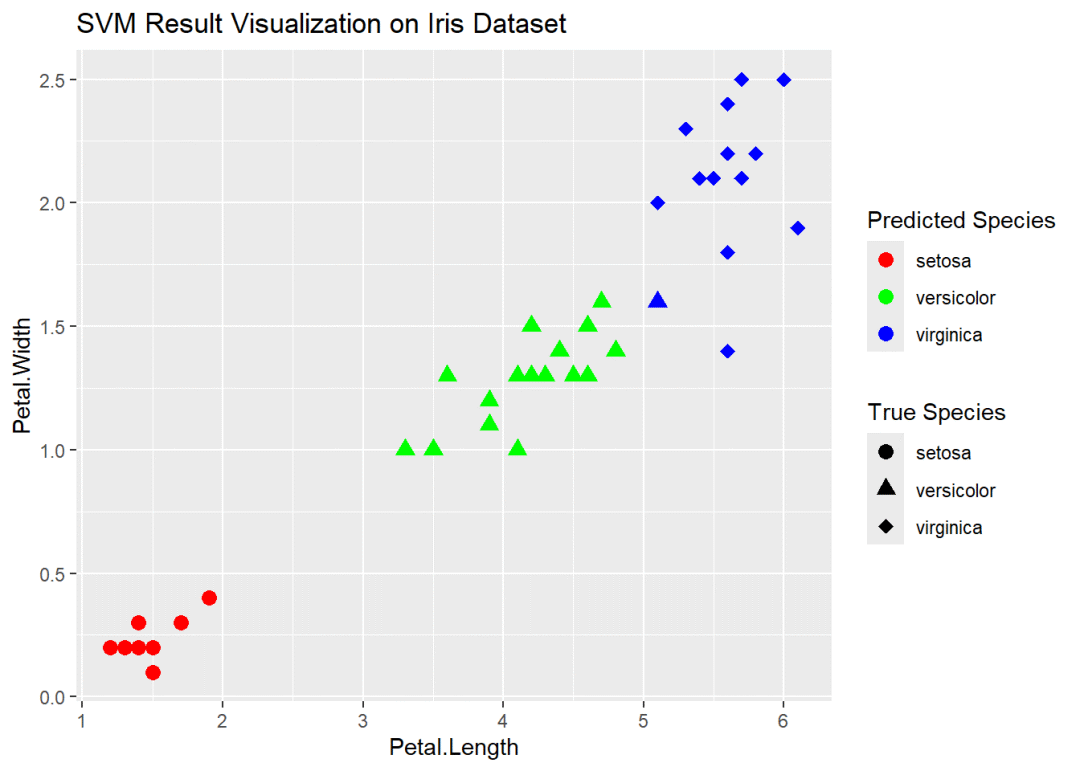
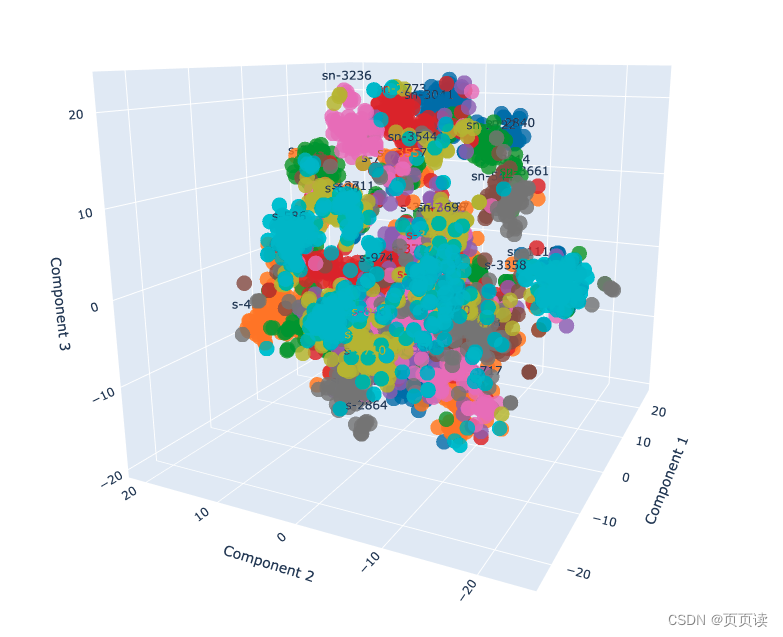
使用情景：比如说现在我有一批numpy的多维向量，比如说都是256维度的，X.shape(n, 256), 已知它们都是经过训练能够在256dim的超球面上实现分类或聚类的，现在我想把它们可视化出来看看各个簇在超球面上的分布是怎样的？

1. 可视化方法介绍(附代码)

为了可视化高维数据（比如你的256维向量）在低维空间（通常是2D或3D）的分布，常用的方法包括主成分分析（PCA）和t-SNE。这两种方法可以帮助我们理解数据在高维空间中的内在结构。

下面，我会展示如何使用Python的scikit-learn库和matplotlib来可视化这些向量。我将使用PCA和t-SNE两种方法来降维，并在3D平面上展示结果。如果你有标签数据，这将有助于我们看到不同簇的分布。

首先，确保你已经安装了必要的库：

pip install numpy matplotlib scikit-learn plotly

下面是一个示例脚本，展示如何将你的高维数据可视化：

# -*- coding: utf8 -*-
import os
import numpy as np
import matplotlib.pyplot as plt
plt.switch_backend('agg')
from sklearn.decomposition import PCA
from sklearn.manifold import TSNE
import plotly.graph_objects as go


def visualize_data_3d_interactive_v0(X, save_path, labels=None):
    """
	X: shape(num, dim)
	"""
    save_path = os.path.splitext(save_path)[0]
    
    # 使用PCA将数据降到3维
    print('PCA is processing ...')
    pca = PCA(n_components=3)
    X_pca = pca.fit_transform(X)
    
    # 使用t-SNE将数据降到3维
    print('t-SNE is processing ...')
    tsne = TSNE(n_components=3, perplexity=30, learning_rate=200)
    X_tsne = tsne.fit_transform(X)
    
    # 为PCA结果创建一个3D散点图
    fig_pca = go.Figure(data=[go.Scatter3d(
        x=X_pca[:, 0], y=X_pca[:, 1], z=X_pca[:, 2],
        mode='markers',
        marker=dict(
            size=5,
            color=labels,                # 设置颜色为标签
            opacity=0.8
        )
    )])
    fig_pca.update_layout(title='PCA Results', scene=dict(
                    xaxis_title='Component 1',
                    yaxis_title='Component 2',
                    zaxis_title='Component 3'))
    fig_pca.write_html(save_path + '_pca.html')
    
    # 为t-SNE结果创建一个3D散点图
    fig_tsne = go.Figure(data=[go.Scatter3d(
        x=X_tsne[:, 0], y=X_tsne[:, 1], z=X_tsne[:, 2],
        mode='markers',
        marker=dict(
            size=5,
            color=labels,                # 设置颜色为标签
            opacity=0.8
        )
    )])
    fig_tsne.update_layout(title='t-SNE Results', scene=dict(
                    xaxis_title='Component 1',
                    yaxis_title='Component 2',
                    zaxis_title='Component 3'))
    fig_tsne.write_html(save_path + '_tsne.html')


def visualize_data_3d_interactive_v1(data_dict, save_path):
    """
	版本不同：
	1.输入不同，data_dict是一个{cls: features}；
	2.可视化功能差异，这个版本加入了对于不同cls显示不同颜色，并打上标签；
	"""

    save_path = os.path.splitext(save_path)[0]
    
    # 准备空列表来存储所有数据点和颜色
    all_data = []
    colors = []
    pid_index = 0  # 用于为每个pid分配不同的颜色
    texts = []  # 用于存储文本标签
    
    # 提取颜色映射
    color_palette = plt.cm.get_cmap('tab10', len(data_dict))
    
    # 将每个pid的数据点收集到一起，并为第一个特征添加标签
    for pid, features in data_dict.items():
        all_data.append(features)
        colors.extend([color_palette(pid_index)] * features.shape[0])
        # 初始化所有文本为空，除了第一个特征
        texts.extend([""] * features.shape[0])
        texts[len(texts) - features.shape[0]] = pid  # 为第一个特征设置pid标签
        pid_index += 1
    
    # 将所有数据合并成一个大矩阵
    all_data = np.vstack(all_data)
    
    # 使用PCA将数据降到3维
    print('PCA is processing ...')
    pca = PCA(n_components=3)
    X_pca = pca.fit_transform(all_data)
    
    # 使用t-SNE将数据降到3维
    print('t-SNE is processing ...')
    tsne = TSNE(n_components=3, perplexity=30, learning_rate=200)
    X_tsne = tsne.fit_transform(all_data)
    
    # 创建一个3D散点图显示PCA结果
    fig_pca = go.Figure(data=[go.Scatter3d(
        x=X_pca[:, 0], y=X_pca[:, 1], z=X_pca[:, 2],
        mode='markers+text',
        text=texts,
        marker=dict(
            size=5,
            color=['rgb({}, {}, {})'.format(c[0]*255, c[1]*255, c[2]*255) for c in colors],  # 将颜色转换为plotly格式
            opacity=0.8
        )
    )])
    fig_pca.update_layout(title='PCA Results', scene=dict(
        xaxis_title='Component 1',
        yaxis_title='Component 2',
        zaxis_title='Component 3'))
    fig_pca.write_html(save_path + '_pca.html')
    
    # 创建一个3D散点图显示t-SNE结果
    fig_tsne = go.Figure(data=[go.Scatter3d(
        x=X_tsne[:, 0], y=X_tsne[:, 1], z=X_tsne[:, 2],
        mode='markers+text',
        text=texts,
        marker=dict(
            size=5,
            color=['rgb({}, {}, {})'.format(c[0]*255, c[1]*255, c[2]*255) for c in colors],  # 将颜色转换为plotly格式
            opacity=0.8
        )
    )])
    fig_tsne.update_layout(title='t-SNE Results', scene=dict(
        xaxis_title='Component 1',
        yaxis_title='Component 2',
        zaxis_title='Component 3'))
    fig_tsne.write_html(save_path + '_tsne.html')



if __name__ == '__main__':
    # test v0
    data_np = np.random.rand(100, 256)
    visualize_data_3d_interactive_v0(data_np, 'outputs/vis_hdim_vector_interactive_v0.html')

    # test v1
    data_dict = {
        'class1': np.random.randn(100, 50),   # 100个50维的样本
        'class2': np.random.randn(100, 50),   # 另外100个50维的样本
        'class3': np.random.randn(100, 50),   # 另外100个50维的样本
        'class4': np.random.randn(100, 50),   # 另外100个50维的样本
        'class5': np.random.randn(100, 50),   # 另外100个50维的样本
        'class6': np.random.randn(100, 50),   # 另外100个50维的样本
        'class7': np.random.randn(100, 50),   # 另外100个50维的样本
        'class8': np.random.randn(100, 50),   # 另外100个50维的样本
        'class9': np.random.randn(100, 50),   # 另外100个50维的样本
        'class10': np.random.randn(100, 50)   # 另外100个50维的样本
    }

    visualize_data_3d_interactive_v1(data_dict, 'outputs/vis_hdim_vector_interactive_v1.html')

在这个脚本中，你需要替换X为你实际的数据。

PCA通常用于获取数据的主要方向，而t-SNE更擅长在保持局部结构的同时展示数据的簇状分布。视觉效果上，t-SNE可能更适合展示复杂的簇结构，但它的计算成本通常也更高。

2. t-SNE 原理

t-SNE（t-Distributed Stochastic Neighbor Embedding）是一种非常流行的机器学习算法，主要用于高维数据的可视化。它由Laurens van der Maaten和Geoffrey Hinton在2008年提出。t-SNE的核心优势在于它能够有效地在二维或三维空间中展示高维数据的局部结构，使得类似的数据点在低维空间中彼此靠近，而不相似的数据点则远离。这使t-SNE特别适用于高维数据的聚类分析和可视化。

t-SNE的工作原理

t-SNE的工作过程可以分为以下几个关键步骤：

1. 计算高维空间中的相似性：
   t-SNE首先在高维空间中计算每对数据点间的条件概率，这种概率反映了一个点选择另一个点作为其邻居的可能性。这个概率由高斯分布（正态分布）的相似性函数决定，其中中心点是数据点本身。

2. 计算低维空间中的相似性：
   对于映射到低维空间中的数据点，t-SNE使用了一个长尾分布——具体来说是t分布（自由度为1的学生t分布，形状类似柯西分布），来计算低维空间中点之间的相似性。使用长尾分布是为了解决所谓的“拥挤问题”（crowding problem），即在低维空间中很难准确地表示原高维空间中的距离关系。

3. 最小化Kullback-Leibler散度：
   t-SNE的目标是使得两个空间（高维和低维）中的概率分布尽可能相似。为此，它通过最小化高维空间与低维空间中定义的概率分布之间的Kullback-Leibler散度来调整低维空间中的点。Kullback-Leibler散度是一种衡量两个概率分布差异的方法。

4. 梯度下降：
   t-SNE使用梯度下降法来找到低维空间的最优配置，以最小化Kullback-Leibler散度。这一步通常需要多次迭代，且对初始值和超参数（如学习率和困惑度）比较敏感。

t-SNE的使用注意事项

• 困惑度（Perplexity）：
  困惑度是t-SNE中的一个重要参数，反映了考虑的邻居的数量，并且对结果有显著影响。一般需要通过试验来选择最合适的困惑度值。

• 随机性：
  由于梯度下降的初始点是随机选择的，t-SNE的结果可能每次都略有不同。为了得到可重复的结果，需要固定随机种子。

• 计算成本：
  t-SNE的计算成本随着数据量的增加而显著增加，特别是对于非常大的数据集，可能需要较长的计算时间。

t-SNE是一个非常强大的工具，特别是在探索性数据分析和数据可视化方面。然而，正确地使用t-SNE需要对其参数和数据特性有一定的理解。

3. PCA 原理

主成分分析（PCA，Principal Component Analysis）是一种广泛使用的统计技术，用于数据降维和探索性数据分析。通过PCA，可以从多维数据集中提取出关键信息，并且以维数更少的数据集形式呈现，这种转换是通过保留数据的最大方差来实现的。

PCA的工作原理

1. 标准化数据：
   首先，通常需要将数据进行标准化处理，即对每个特征维度进行中心化（减去均值）和缩放（除以标准差），以使各特征具有相同的重要性。

2. 计算协方差矩阵：
   然后，计算数据的协方差矩阵。协方差矩阵描述了数据中各个变量之间的相关性；在这个矩阵中，每个元素是对应两个变量的协方差，它反映了两个变量变化时是如何相互影响的。

3. 求解特征值和特征向量：
   对协方差矩阵进行特征值分解，求得的特征值和对应的特征向量指示了数据的主要变化方向。特征值越大，对应的特征向量在数据集中的重要性就越高，这个特征向量定义了一个主成分。

4. 选择主成分：
   选择最大的几个特征值及其对应的特征向量。通常，这些特征向量被称为“主成分”，它们是新的、较少的、互相正交的坐标轴，这些坐标轴是按照它们能够捕捉的数据方差的重要性排序的。

5. 构造新的特征空间：
   将原始数据投影到这些选定的主成分上，得到的就是降维后的数据。这一步通常涉及到一个矩阵乘法运算，原始数据矩阵乘以选定的主成分矩阵。

PCA的应用

• 数据压缩：通过减少数据集的维数，PCA有助于减少存储空间和提高算法效率。
• 去噪：PCA可以帮助识别并去除数据中的噪声，特别是当噪声较小且数据的主要结构在高方差的方向时。
• 可视化：在多维数据集中，通过PCA可以将数据降到两维或三维，使得数据可通过图形化方式展示。

注意事项

虽然PCA是一个强大的工具，但它也有局限性。由于PCA是基于线性假设的，它可能无法有效识别基于非线性结构的复杂模式。此外，如果所有变量的方差都差不多，PCA的效果可能就不明显。在这些情况下，可能需要考虑使用其他的降维技术，如t-SNE、LDA（线性判别分析）或者基于核的PCA方法。