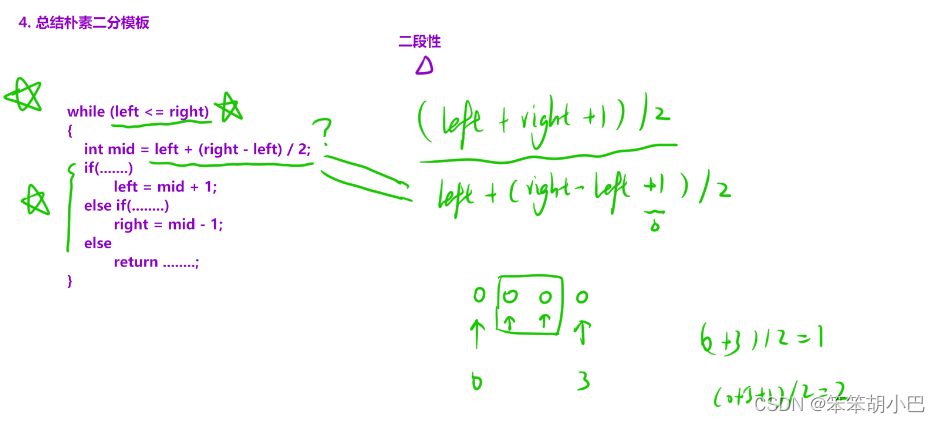
17. 二分查找(easy)

算法流程:


算法代码:
int search(int* nums, int numsSize, int target)
{
// 初始化 left 与 right 指针
int left = 0, right = numsSize - 1;
// 由于两个指针相交时,当前元素还未判断,因此需要取等号
while (left <= right)
{
// 先找到区间的中间元素
int mid = left + (right - left) / 2;
// 分三种情况讨论
if (nums[mid] == target) return mid;
else if (nums[mid] > target) right = mid - 1;
else left = mid + 1;
}
// 如果程序⾛到这⾥,说明没有找到⽬标值,返回 -1
return -1;
}总结朴素二分模板
18. 在排序数组中查找元素的第⼀个和最后⼀个位置(medium)

算法思路:

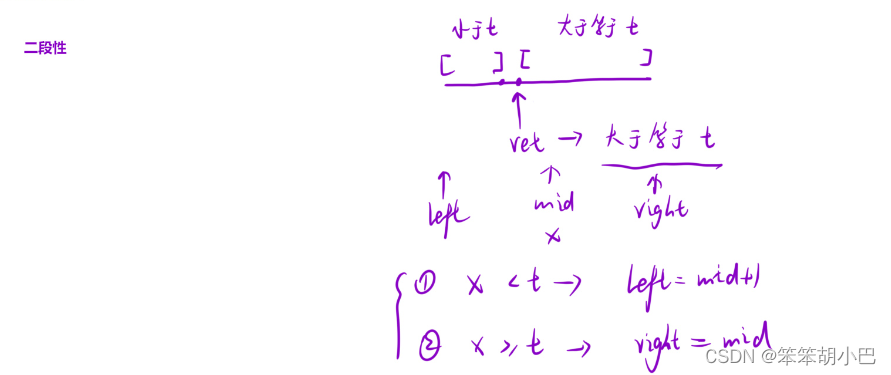
寻找左边界思路:


寻找右边界思路:


⼆分查找算法总结:

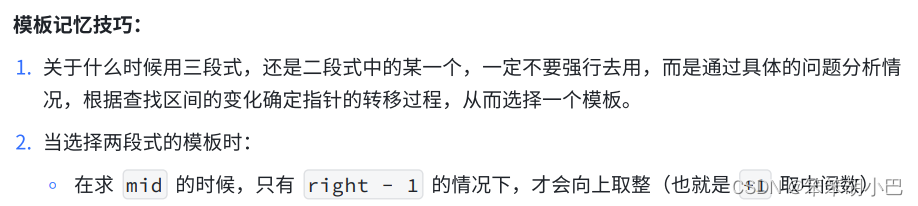
模板记忆技巧:
C++ 算法代码:
class Solution
{
public:
vector<int> searchRange(vector<int>& nums, int target)
{
// 处理边界情况
if (nums.size() == 0) return { -1, -1 };
int begin = 0;
// 1. ⼆分左端点
int left = 0, right = nums.size() - 1;
while (left < right)
{
int mid = left + (right - left) / 2;
if (nums[mid] < target) left = mid + 1;
else right = mid;
}
// 判断是否有结果
if (nums[left] != target) return { -1, -1 };
else begin = left; // 标记⼀下左端点
// 2. ⼆分右端点
left = begin, right = nums.size() - 1;
while (left < right)
{
int mid = left + (right - left + 1) / 2;
if (nums[mid] <= target) left = mid;
else right = mid - 1;
}
return { begin, right };
}
};19. 搜索插⼊位置(easy)

解法(⼆分查找算法):

C++ 算法代码:
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int left = 0;
int right = nums.size() - 1;
while(left < right)
{
int mid = left + (right - left) / 2;
if(nums[mid] < target)
left = mid + 1;
else
right = mid;
}
if(nums[left] < target) return right + 1;
return left;
}
};20. x 的平⽅根(easy)
解法⼀:(暴⼒查找)


C++ 算法代码:
class Solution{
public:
int mySqrt(int x) {
// 由于两个较⼤的数相乘可能会超过 int 最⼤范围
// 因此⽤ long long
long long i = 0;
for (i = 0; i <= x; i++)
{
// 如果两个数相乘正好等于 x,直接返回 i
if (i * i == x) return i;
// 如果第⼀次出现两个数相乘⼤于 x,说明结果是前⼀个数
if (i * i > x) return i - 1;
}
// 为了处理oj题需要控制所有路径都有返回值
return -1;
}
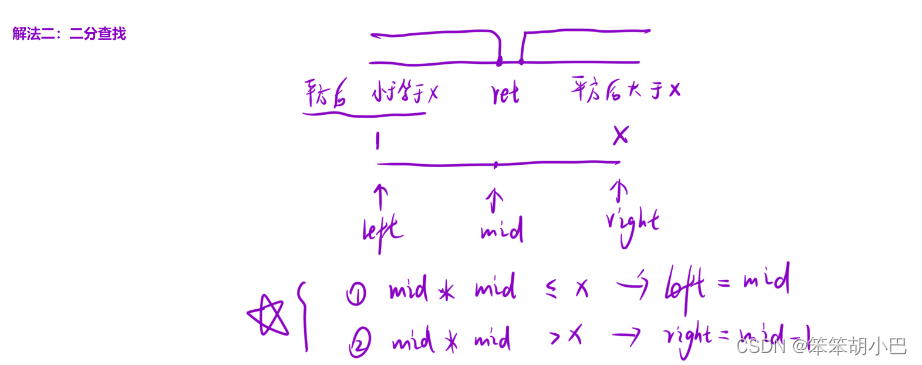
};解法⼆(⼆分查找算法):

C++ 算法代码:
class Solution
{
public:
int mySqrt(int x)
{
if (x < 1) return 0; // 处理边界情况
int left = 1, right = x;
while (left < right)
{
long long mid = left + (right - left + 1) / 2; // 防溢出
if (mid * mid <= x) left = mid;
else right = mid - 1;
}
return left;
}
};
21. 山峰数组的峰顶(easy)

解法⼀(暴⼒查找):

算法代码:
class Solution {
public:
int peakIndexInMountainArray(vector<int>& arr) {
int n = arr.size();
// 遍历数组内每⼀个元素,直到找到峰顶
for (int i = 1; i < n - 1; i++)
// 峰顶满⾜的条件
if (arr[i] > arr[i - 1] && arr[i] > arr[i + 1])
return i;
// 为了处理 oj 需要控制所有路径都有返回值
return -1;
}
};
解法⼆(⼆分查找):


算法代码:
class Solution {
public:
int peakIndexInMountainArray(vector<int>& arr) {
int left = 1;
int right = arr.size() - 2;
while(left < right)
{
int mid = left + (right - left + 1) / 2;
if(arr[mid] > arr[mid - 1])
left = mid;
else
right = mid - 1;
}
return left;
}
};22. 寻找峰值(medium)

解法⼆(⼆分查找算法):


C++ 算法代码:
class Solution {
public:
int findPeakElement(vector<int>& nums) {
int left = 0, right = nums.size() - 1;
while (left < right)
{
int mid = left + (right - left) / 2;
if (nums[mid] > nums[mid + 1]) right = mid;
else left = mid + 1;
}
return left;
}
};23. 搜索旋转排序数组中的最⼩值(medium)

解法(⼆分查找):


C++ 算法代码:
class Solution
{
public:
int findMin(vector<int>& nums)
{
int left = 0, right = nums.size() - 1;
int x = nums[right]; // 标记⼀下最后⼀个位置的值
while (left < right)
{
int mid = left + (right - left) / 2;
if (nums[mid] > x) left = mid + 1;
else right = mid;
}
return nums[left];
}
};
24. 0〜n-1 中缺失的数字(easy)

解法(⼆分查找算法):
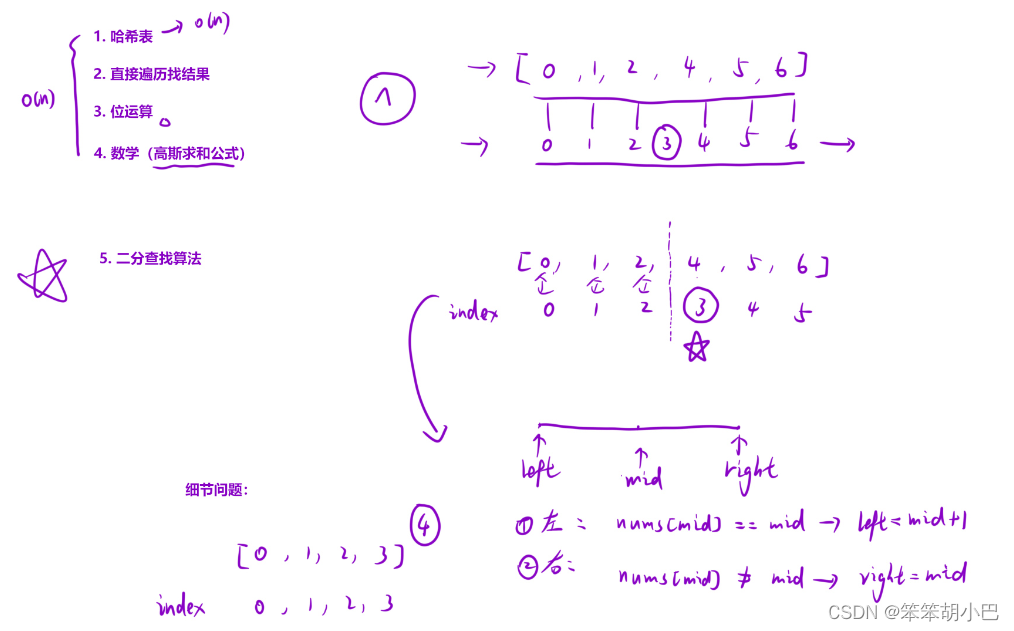

C++ 算法代码:
class Solution {
public:
int missingNumber(vector<int>&nums)
{
int left = 0, right = nums.size() - 1;
while (left < right)
{
int mid = left + (right - left) / 2;
if (nums[mid] == mid) left = mid + 1;
else right = mid;
}
return left == nums[left] ? left + 1 : left;
}
};