01.引言
频率是单位时间内某事件重复发生的次数,用ω表示,单位是赫兹(Hz)。设m时间内某事件重复发生n次,则此事件发生的频率ω为一。又因为周期定义为重复事件发生的最小时间间隔,故频率也可以表示为周期的倒数:ω=n/m,T表示周期。频率是一个很重要的概念,在工程数学中常用于分析信号特征。其最早在地震波的应用中显示优势。从最早的Fourier分析,到改变其整体性而出现的Gabor变换,再到连续小波变换,本章将沿着这条主线,介绍小波分析出现的全过程。
02.主要内容
1.基于Fourier分析的频谱图
fun = @(x)0.*(x<0 |x>5)+x.*(x>=0 & x<1)+1.*(x>=1 & x<4) +(5-x).*(x>=4 & x<5);%分段函数
x=-5:0.2:10;%x自变量
y=fun(x);%得到输入的平稳信号y
Dfy = fft(y);%离散Fourier变换
Dfy_shift = fftshift(Dfy); %对称变换得到对称的Fourier频谱
figure
plot(y); axis([0,80,-0.05,1.05]),xlabel('n'),ylabel('y');%原始平稳信号
figure
plot(abs(Dfy)),xlabel('n'),ylabel('|Dfy|');%|Dft|为离散频谱幅值信息
figure
plot(abs(Dfy_shift)),xlabel('n'),ylabel('|Dfy|');%对称变换后的频谱

2.基于Gabor变换的平面频谱图
%主函数:Gabor变换频谱
x=-5:0.2:10;%x自变量
a = 1; %Gauss窗口函数的窗口大小参数
b = -5:0.2:10; %平移参数,一般为原始信号长度。
Dfy = zeros(length(b),length(b));
for i = 1:length(b)
GDfy(i,:) = fft(Gb_fun(a,b(i),x));%针对不同的b的离散Fourier变换
GDfy_shift(i,:) = fftshift(GDfy(i,:));%平移频率中心
end
%绘制频谱立体图和图像
figure
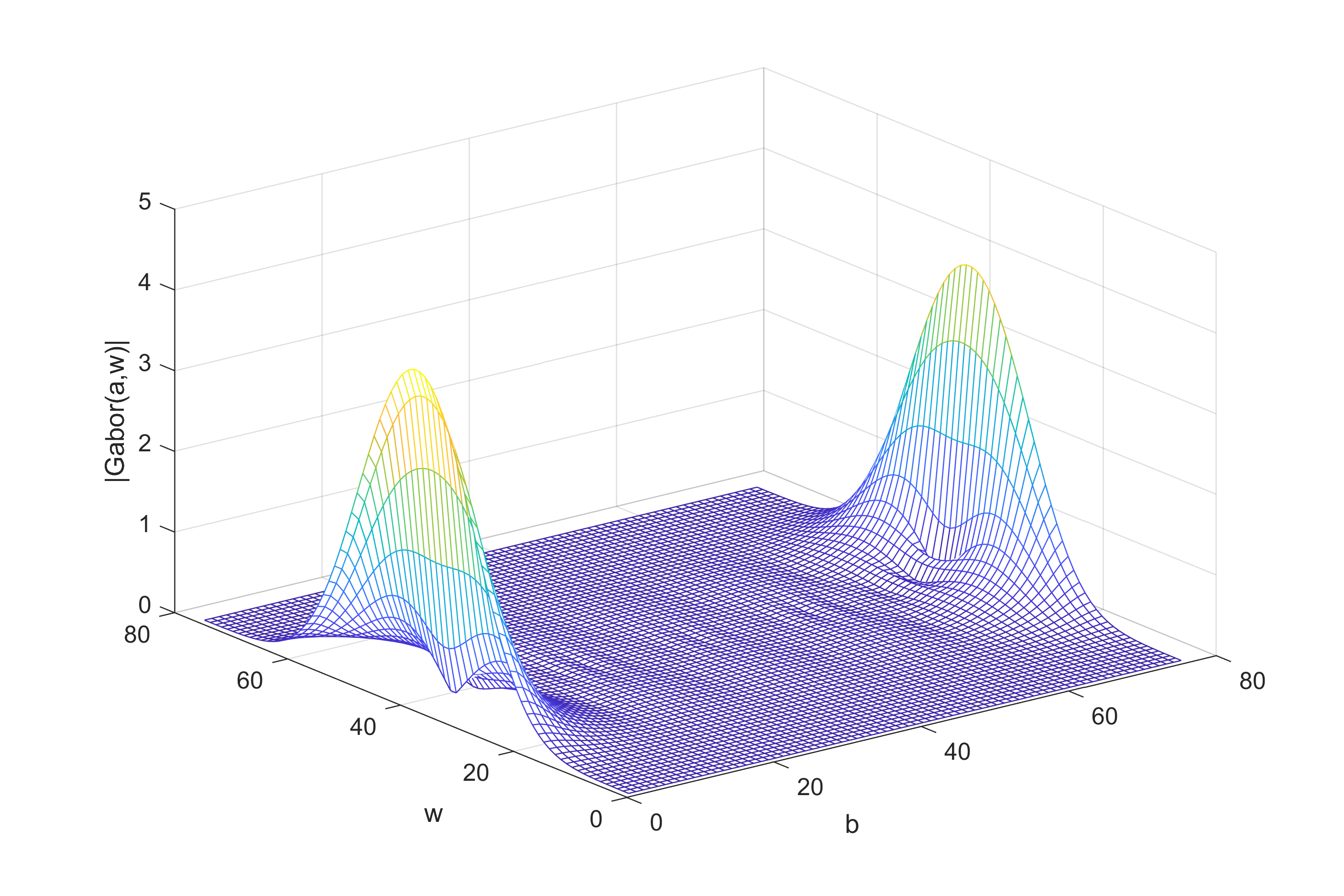
mesh(abs(GDfy)); xlabel('b'),ylabel('w'),zlabel('|Gabor(a,w)|');
figure
imshow(abs(GDfy));
imwrite(abs(GDfy),'Fig2-4(b)ImGabor.jpg','jpg')
%绘制对称变换后的频谱立体图和图像
figure
mesh(abs(GDfy_shift)); xlabel('b'),ylabel('w'),zlabel('|Gabor(a,w)|');
figure
imshow(abs(GDfy_shift));
imwrite(abs(GDfy_shift),'Fig2-5(b)ImGaborShift.jpg','jpg')



3.基于连续小变换的频谱
%针对同一个分段函数,我们采用“Haar“小波分解,得到小波的频谱
fun = @(x)0.*(x<0 |x>5)+x.*(x>=0 & x<1)+1.*(x>=1 & x<4) +(5-x).*(x>=4 & x<5);%分段函数
x=-5:0.2:10;%x自变量
y = fun(x);
figure
Cab = cwt(y,1:2:32,'haar','3Dplot');%连续小波变换,并进行频谱幅值的三维显示
figure
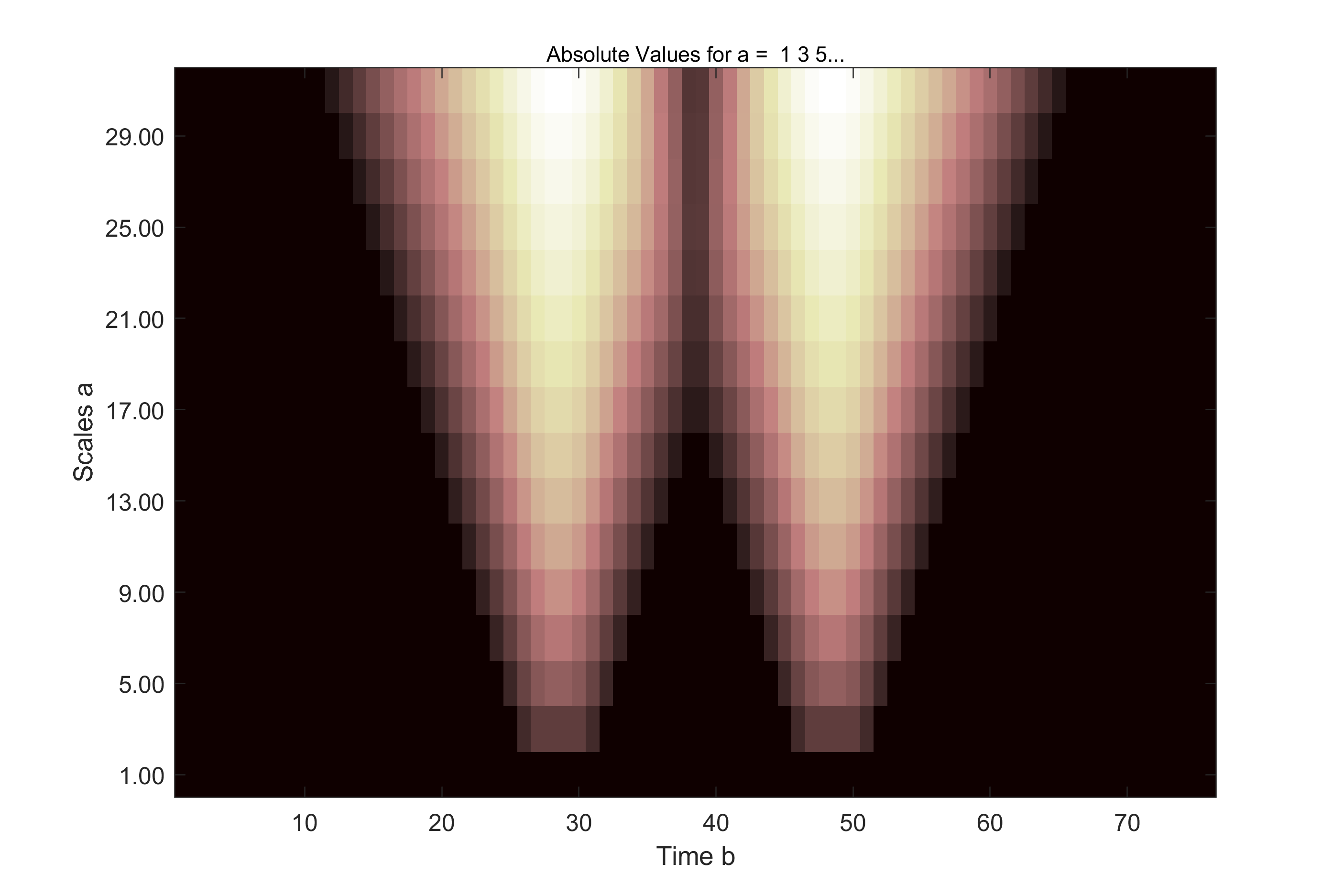
Cab = cwt(y,1:2:32,'haar','plot');%连续小波变换,并进行频谱幅值的图像显示
%这段程序也可以按照Gabor变换的方式显示,即
a = 1:2:32;
b = 1:length(y);
Cab = cwt(y,1:2:32,'haar');%连续小波变换,并进行频谱幅值的三维显示
figure
mesh(b,a,abs(Cab)),xlabel('b'),ylabel('a'),zlabel('|Cab|');
figure
imshow(abs(Cab));
imwrite(abs(Cab),'Fig2-6(d)Cwt.jpg','jpg')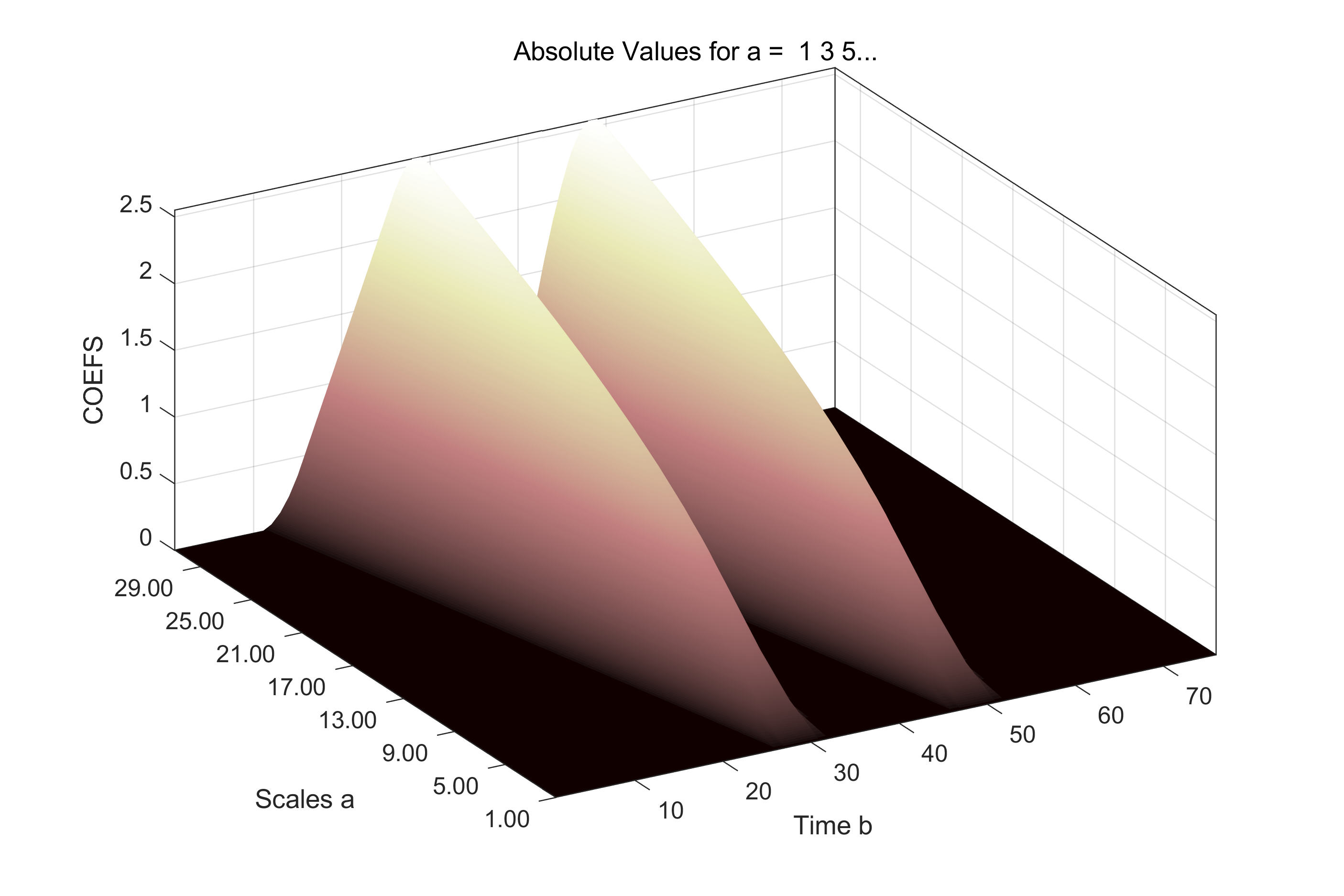



4.基于离散小波变换频谱
fun = @(x)0.*(x<0 |x>5)+x.*(x>=0 & x<1)+1.*(x>=1 & x<4) +(5-x).*(x>=4 & x<5);%分段函数
%为离散小波实现做准备,此处采样值加细为2^-5。
x=-5:2^(-5):10;%x自变量
y = fun(x);
%二进小波实现,离散a,不离散b
k = -5:5;
a = 2.^k;
figure
djb = cwt(y,a,'haar','3Dplot');%连续小波变换在2进制点处取值,并进行频谱幅值的三维显示
figure
djb = cwt(y,a,'haar','plot');% 连续小波变换在2进制点处取值,并进行频谱幅值的图像显示
%离散小波实现,直接取djb的平移的整数点值。
n = -5:10;%平移整数点值
b_k = ones(length(n),length(a));%平移整数点在对应的自变量x中的位置序号
for i = 1:length(a)
for j = 1:length(n)
an = a(i)*n(j);%整平移,对应的连续小波变换中的实际平移,即b = a*n,
if(an>=-5 & an <=10 )
b_k(i,j) = find(an == x);%找到对应实际平移的位置序号
djk(i,j) = djb(i, b_k(i,j));%对应连续小波变换中的离散取值
end
end
end
figure
imshow(djk),colormap(pink);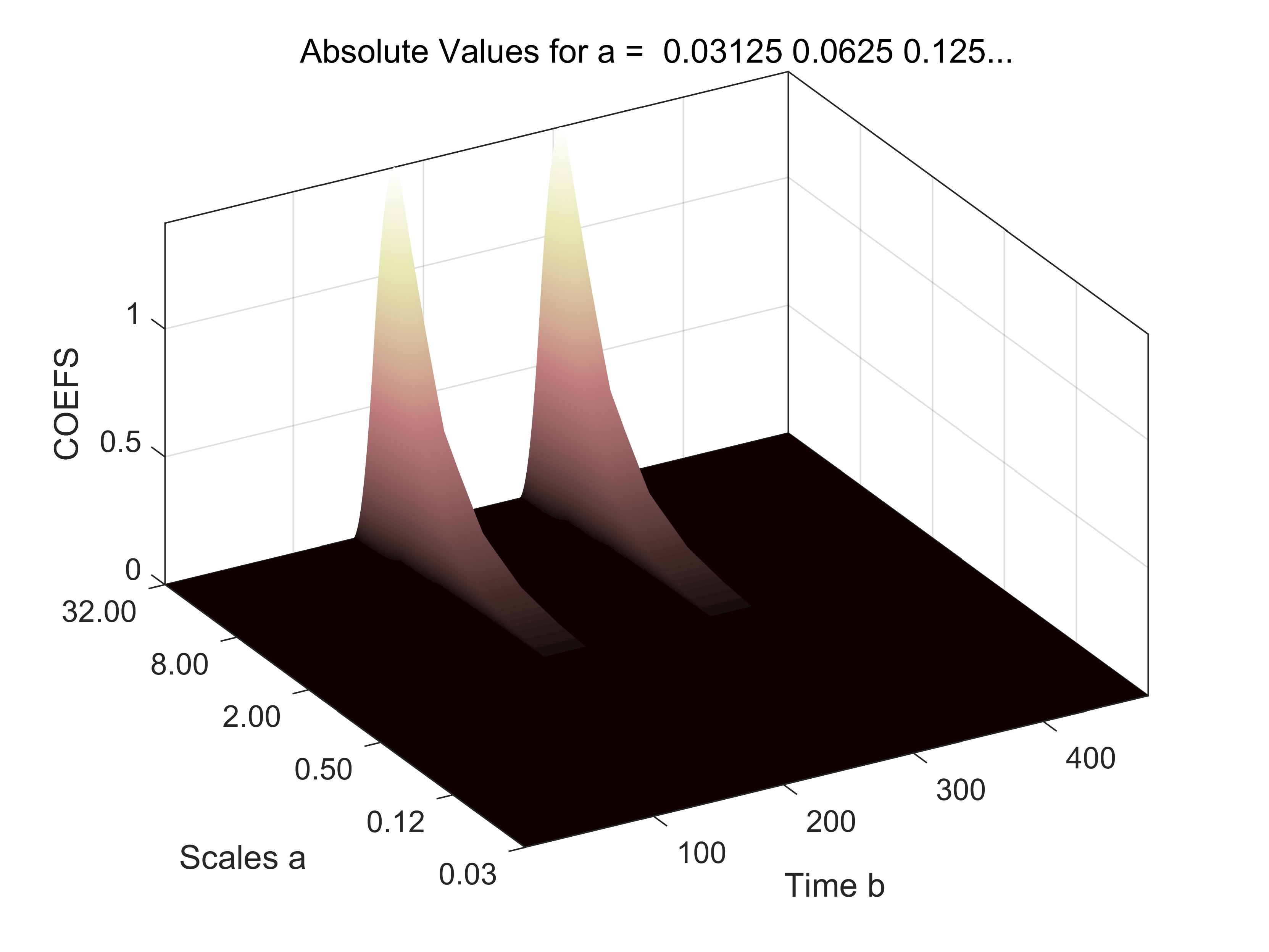

03.实例:音频信号的频谱特征提取
1. 加载数据
load data1 c1
load data2 c2
load data3 c3
load data4 c4这些代码加载了四个不同类别的音频数据,分别存储在 c1、c2、c3、c4 中。
2. 连续小波变换(CWT)
for i = 1: m
d(1,i,:,:) = cwt(c1(i,:),a,'haar');
d(2,i,:,:) = cwt(c2(i,:),a,'haar');
d(3,i,:,:) = cwt(c3(i,:),a,'haar');
d(4,i,:,:) = cwt(c4(i,:),a,'haar');
end这个循环对每个音频数据 c1、c2、c3、c4 做连续小波变换,并将结果存储在 d 数组中。a 是尺度因子数组,表示不同的尺度。这里使用 ‘haar’ 小波作为变换基函数。
3. 提取特征
d_value(:,:,:) = sum(d(:,1:m_sample,:,:),2)./m_sample;这一步计算每个类别在前 m_sample 个样本上的连续小波特征的平均值,用于后续的分类。
4. 显示连续小波特征图像
subplot(2,2,1);
imshow(dd1,[]);title('data1');
subplot(2,2,2);
imshow(dd2,[]); title('data2');
subplot(2,2,3);
imshow(dd3,[]); title('data3');
subplot(2,2,4);
imshow(dd4,[]); title('data4');这部分将四类音乐的平均连续小波特征图像显示在一个 2x2 的子图中,并存储为图片文件。
5. 分类识别
for i = 1:4
for k = m_sample+1:m
mk = k-m_sample;
for j = 1:4
d1(:,:) = d(i,k,:,:);
d2(:,:) = d_value(j,:,:);
r = norm(d1-d2,2);
if(r < m_min(mk,i))
m_min(mk,i)= r;
mk_i = j;
end
end
if(i == mk_i)
m_right (i)= m_right(i) + 1;
end
end
end这部分代码用于识别测试集中的样本。对于每个测试样本,计算其与每个类别的平均连续小波特征的欧氏距离,并选择距离最小的类别作为预测类别。最后统计每个类别的识别正确数量。
结果输出
m_score = m_right./m_test
score = sum(m_score)./4计算并输出每个类别的识别率(正确识别数除以总测试样本数),以及所有类别的平均识别率。