树
树是n个结点的有限集合,当n=0时为空树,在任意一颗非空的树中,有且只有一个特定的称为根的结点,当n>1时,其余结点又可以分为m个不相交的有限集,其中每一个集合又是一棵树,并且称为根的子树
树的结点包含一个数据元素以及若干指向其子树的分支,结点拥有的子树称为结点的度,度为0的结点称为叶结点或者终端结点,度不为0的结点称为非终端结点或者分支结点,除根结点之外,分支结点称为内部结点,树的度是树内部各个结点的度的最大值
结点的子树的根称为该结点的孩子,该结点称为孩子的双亲,同一个双亲的孩子之间互相称为兄弟
树的深度:树中结点的最大层次
树的存储结构
- 顺序存储结构
- 链式存储结构
二叉树
对于在某个阶段都是两种结果的情形,比如开关,01,上下,对错,真假等,都适合使用树状结构来进行建模,这种树被称为二叉树
》》二叉树特点
- 每个节点必须有两颗子树
- 左子树和右子树是有顺序的,次序不能颠倒
- 要能够区分左子树和右子树
二叉树的基本形态
- 空二叉树
- 只有一个根结点
- 根结点只有左子树
- 根结点只有右子树
- 根结点既有左子树也有右子树
特殊二叉树
1.斜树:所有的结点都只有左子树的二叉树称为左斜树,所有结点都只有右子树的二叉树称为右斜树
2.满二叉树:在一颗二叉树中,所有的分支结点都存在左子树和右子树,并且所有的叶子结点都在同一层次上,这样的二叉树称为满二叉树

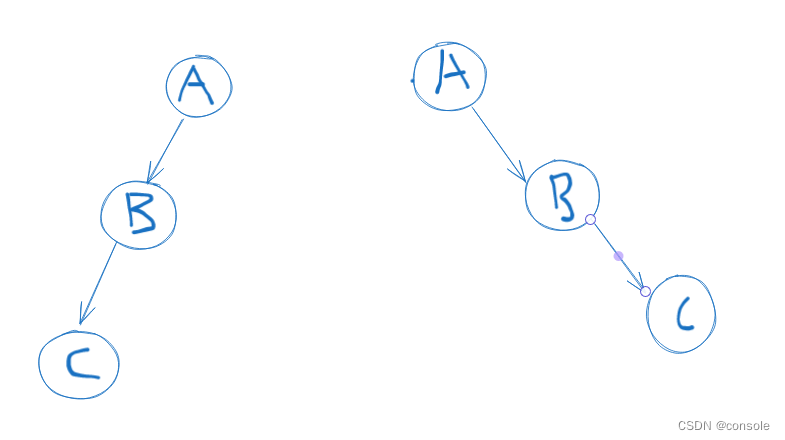
3.完全二叉树:对于一颗具有n个结点的二叉树按照层次编号,如果编号为i的结点与同样深度的满二叉树中编号为i的结点在二叉树中的位置完全相同,那么这颗二叉树称为完全二叉树

此时左边的为完全二叉树,而右边的不是,因为节点的编号不是连续的,C缺少了左子树
完全二叉树特点:
- 叶子结点只能出现在最下面两层
- 最下面的叶子一定集中在左部的连续位置
- 倒数第二层,如果有叶子结点,一定都在右边连续的位置
- 如果结点的度为1,那么该结点只有左子树
- 同样的二叉树,完全二叉树的深度最小
二叉树的性质
- 在二叉树的第i层至多有2^(i-1)个结点
- 深度为k的二叉树至多有2^(k-1)个结点
- 对于任何一颗二叉树,如果其终端节点数为n,度为2的节点数为m,则n=m+1
》》二叉树的顺序存储结构
虽然顺序结构对于树这种一对多的关系结构实现起来比较困难,但是二叉树具有特殊性,二叉树的结点是按照特定的顺序进行编号的,因此可以使用顺序存储结构也可以实现二叉树,但是考虑的特殊情况(每个结点只有右子树),就会造成内存空间的极大浪费,因此顺序存储结构一般只适用于完全二叉树
二叉树的链式存储结构
二叉树的节点
为二叉树的每个结点都设置两个指针域和一个数据域,分别用来指向其子树和存储数据
其中data就为二叉树节点的数据域,存储节点的数据
ltree和rtree为指针域,分别指向其左子树和右子树
二叉树的遍历方法
1.前序遍历
如果二叉树为空,则返回空,否则返回根结点,否则前序遍历左子树,再前序遍历右子树
只要传入的二叉树不为空,则打印出当前节点的值,再递归调用函数遍历其左子树,最后递归调用函数遍历其又子树
2.中序遍历
如果二叉树为空,则返回空,否则中序遍历左子树,访问根结点,再中序遍历右子树
3.后序遍历
如果二叉树为空,则返回空,否则后序遍历左子树,后序遍历右子树,访问根结点
4.层次遍历
如果二叉树为空,则返回空,否则从根结点开始,从上往下逐层遍历,在同一层中,按照从左到右的顺序进行访问
这是通过队列来实现的
二叉树遍历性质
- 已知一个中序遍历和前序遍历可以确定唯一的二叉树
- 已知一个中序遍历和后序遍历可以确定唯一的二叉树
注:如果已知前序和后序遍历是不能确定一颗二叉树的
二叉树的建立
使用补空法建立二叉树,如果结点为#,则该节点为空
建立二叉树算法:
- 首先捕获一个值,判断是否为#,如果为#,二叉树为空
- 否则循环捕获节点信息,为结点分配内存,分配失败则退出
- 递归创造左右结点
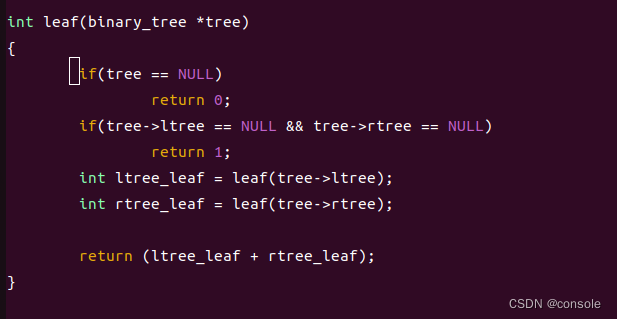
二叉树的叶子数,深度,以及节点数
叶子数:只要该节点没有左右子树,那么该节点就为二叉树叶子
深度:找出左右子树的最大深度,再加上根节点,就是该叶子数的深度
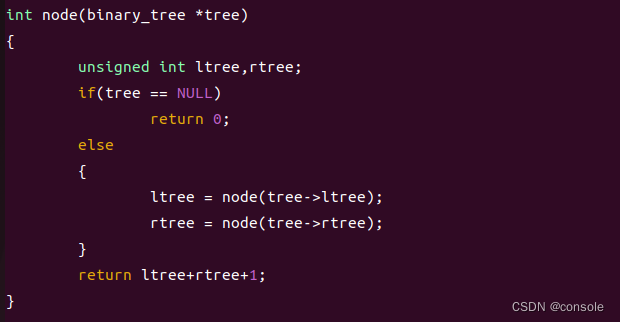
节点数:求出根节点左子树的节点数和右子树的节点数,再加上根节点就是该二叉树的节点数
线索二叉树
指向前驱和后继的指针称为线索,加上线索的二叉链表称为线索链表,相应的二叉树称为线索二叉树,对二叉树以某种次序遍历使得其变为线索二叉树的过程称为线索化
线索化的实质就是将二叉树的空指针改为指向前驱或者后继的线索,由于前驱和后继的信息只能在遍历的过程中得到,所以线索化的过程就是修改空指针的过程
对于n个结点的二叉树,一共有2n个指针域,而真正使用的指针域只有n-1个,有n+1个指针域没有被利用,因此可以将空指针域的内容填充,让其指向其前驱点或后继
线索二叉树实现
需要两个变量来确定,二叉树的指针域是指向为其子树还是指向其前驱点
设为ltag,rtag,这两个变量为bool类型
当ltag为0时指向该结点的左子树,当ltag为1时指向该结点的前驱
当rtag为0时指向该结点的右子树,当rtag为1时指向该结点的后继
意义
如果所使用的二叉树需要经常进行遍历或者查找某些结点时需要某种遍历序列中的前驱和后继,那么采用线索二叉树