大家知道动规是由前一个状态推导出来的,而贪心是局部直接选最优的,对于刷题来说就够用了。
对于动态规划问题,我将拆解为如下五步曲,这五步都搞清楚了,才能说把动态规划真的掌握了!
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
part 02
不同路径
63. 不同路径 II - 力扣(LeetCode)

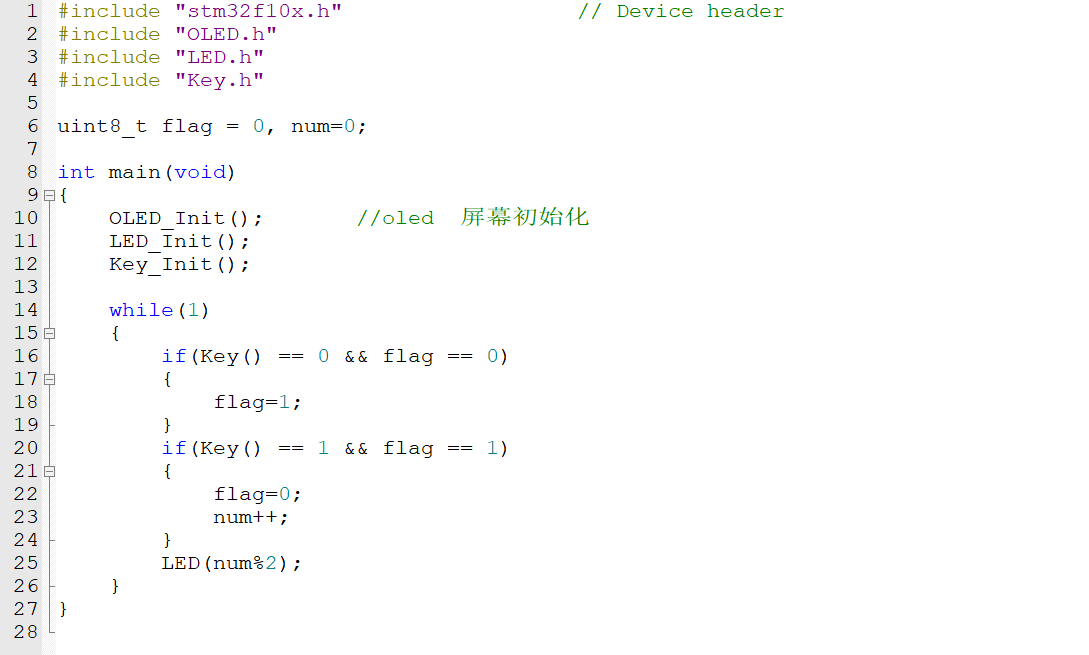
//初始化(优化)
for(int j=1;j<=n && obstacleGrid[0][j-1]==0;j++)
{
dp[1][j]=1;
}
for(int i=1;i<=m && obstacleGrid[i-1][0]==0 ;i++)
{
dp[i][1]=1;
}
part 03
343. 整数拆分 - 力扣(LeetCode)
- dp[i] 拆分数字i,得到最大乘积dp[i]
- 递推公式:dp[i] = max({dp[i], (i - j) * j, dp[i - j] * j});
也可以这么理解,j * (i - j) 是单纯的把整数拆分为两个数相乘,而j * dp[i - j]是拆分成两个以及两个以上的个数相乘。
那么在取最大值的时候,为什么还要比较dp[i]呢?
因为在递推公式推导的过程中,为了每次计算更新dp[i] - 初始化 dp[2]=1
- 确定遍历顺序
dp[i] 是依靠 dp[i - j]的状态,所以遍历i一定是从前向后遍历,先有dp[i - j]再有dp[i]。
public int integerBreak(int n) {
int[] dp = new int[n+1];
dp[2]=1;
for(int i=3;i<=n;i++)
{
for(int j=1;j<=i-1;j++)
{
dp[i]=Math.max(dp[i],Math.max(j*(i-j),j*dp[i-j]));
}
}
return dp[n];
}
96. 不同的二叉搜索树 - 力扣(LeetCode)
当1为头结点的时候,其右子树有两个节点,看这两个节点的布局,是不是和 n 为2的时候两棵树的布局是一样的啊!
(可能有同学问了,这布局不一样啊,节点数值都不一样。别忘了我们就是求不同树的数量,并不用把搜索树都列出来,所以不用关心其具体数值的差异)
当3为头结点的时候,其左子树有两个节点,看这两个节点的布局,是不是和n为2的时候两棵树的布局也是一样的啊!
当2为头结点的时候,其左右子树都只有一个节点,布局是不是和n为1的时候只有一棵树的布局也是一样的啊!
发现到这里,其实我们就找到了重叠子问题了,其实也就是发现可以通过dp[1] 和 dp[2] 来推导出来dp[3]的某种方式。
思考到这里,这道题目就有眉目了。
part04
背包问题
0 1背包
求容量为j的背包,最多能装多少(二维数组)
能不能放
- 不能
取上一个值 - 能
取放和不放的最大值
import java.util.ArrayList;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
int m;
int n;
Scanner sc=new Scanner(System.in);
m=sc.nextInt();//材料种类
n=sc.nextInt();//行李空间
int[] weight=new int[m];
int[] value=new int[m];
for (int i = 0; i < m; i++) {
weight[i]=sc.nextInt();
}
for (int i = 0; i < m; i++) {
value[i]=sc.nextInt();
}
//dp[i][j] i表示第i种材料,j表示行李容量,dp[i][j]表示前i种材料放入j空间的最大价值
int[][] dp=new int[m][n+1];
//递推公式 取放i材料,与不放i材料的value最大值 dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i])
//初始化 由递推公式可知,每一个值由左上方的值推导而来.因此初始化第一行第一列
for(int j=weight[0];j<=n;j++)
{
dp[0][j]=value[0];
}
//遍历顺序 从前往后
for(int i=1;i<m;i++)
{
for(int j=1;j<=n;j++)
{
if (j < weight[i]) {
/**
* 当前背包的容量都没有当前物品i大的时候,是不放物品i的
* 那么前i-1个物品能放下的最大价值就是当前情况的最大价值
*/
dp[i][j] = dp[i-1][j];
} else {
/**
* 当前背包的容量可以放下物品i
* 那么此时分两种情况:
* 1、不放物品i
* 2、放物品i
* 比较这两种情况下,哪种背包中物品的最大价值最大
*/
dp[i][j] = Math.max(dp[i-1][j] , dp[i-1][j-weight[i]] + value[i]);
}
}
}
System.out.println(dp[m-1][n]);
}
}
416. 分割等和子集 - 力扣(LeetCode)
分成两个,背包大小为sum/2
part 05
1049. 最后一块石头的重量 II - 力扣(LeetCode)
本题其实就是尽量让石头分成重量相同的两堆,相撞之后剩下的石头最小,这样就化解成01背包问题了。
return int
装满容量为x的背包,有几种方法
494. 目标和 - 力扣(LeetCode)
本题要如何使表达式结果为target,
正数集合和left-负数集合和right=target
left + right = sum,而sum是固定的。right = sum - left
公式来了, left - (sum - left) = target 推导出 left = (target + sum)/2 。
target是固定的,sum是固定的,left就可以求出来。
此时问题就是在集合nums中找出和为left的组合。
此时问题就转化为,装满容量为x的背包,有几种方法n。
之前都是求容量为j的背包,最多能装多少。
return n
474. 一和零 - 力扣(LeetCode)
class Solution {
public int findMaxForm(String[] strs, int m, int n) {
// dp[i][j] i个0,j个1大的容器,最多装元素 dp[i][j]个
//dp[i][j] = Math.max(dp[i][j],dp[i-x][j-y]+1);,x表示装strs[i] 中0的个数古,y表示strs[i] 中1的个数
int zeroNums=0;
int oneNums=0;
int[][] dp=new int[m+1][n+1];
for(String str:strs)
{
zeroNums=0;
oneNums=0;
for(char ch: str.toCharArray())
{
if(ch == '0')
{
zeroNums++;
}else{
oneNums++;
}
}
//倒序遍历
for(int i=m;i>=zeroNums;i--)
{
for(int j=n;j>=oneNums;j--)
{
dp[i][j]=Math.max(dp[i][j],dp[i-zeroNums][j-oneNums]+1);
}
}
}
return dp[m][n];
}
}
没太搞懂
//倒序遍历
for(int i=m;i>=zeroNums;i--)
{
for(int j=n;j>=oneNums;j--)
{
dp[i][j]=Math.max(dp[i][j],dp[i-zeroNums][j-oneNums]+1);
}
}

未完待续