目录

力扣130. 被围绕的区域

解析代码

---

力扣130. 被围绕的区域

130. 被围绕的区域

难度 中等

给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' ，找到所有被 'X' 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。

示例 1：

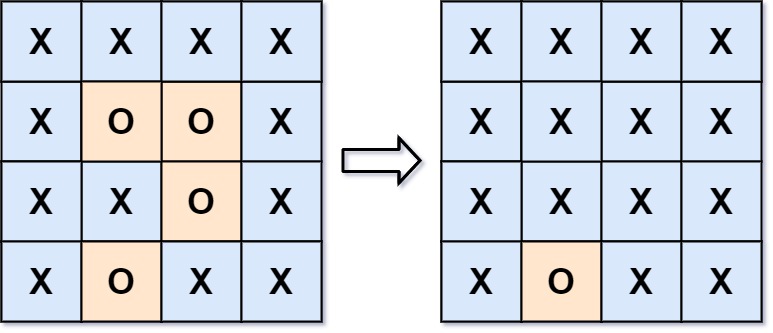
输入：board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
输出：[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
解释：被围绕的区间不会存在于边界上，换句话说，任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上，或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。

示例 2：

输入：board = [["X"]]
输出：[["X"]]

提示：

• m == board.length
• n == board[i].length
• 1 <= m, n <= 200
• board[i][j] 为 'X' 或 'O'

class Solution {
public:
    void solve(vector<vector<char>>& board) {

    }
};

---

解析代码

         正难则反。 可以先利用 bfs 将与边缘相连的 'O' 区域修改成无关字符，然后重新遍历矩阵，将没有标记过的 'O' 全修改成 'X' 即可，再把无关字符全还原成'O'。

class Solution {
    int dx[4] = {0, 0, -1, 1};
    int dy[4] = {1, -1, 0, 0};
    int m = 0, n = 0;

public:
    void solve(vector<vector<char>>& board) {
        m = board.size(), n = board[0].size();
        for(int i = 0; i < n; ++i) // 修改边界的O成无关字符
        {
            if(board[0][i] == 'O')
                bfs(board, 0, i);
            if(board[m - 1][i] == 'O')
                bfs(board, m - 1, i);
        }
        for(int i = 0; i < m; ++i)
        {
            if(board[i][0] == 'O')
                bfs(board, i, 0);
            if(board[i][n - 1] == 'O')
                bfs(board, i, n - 1);
        }

        for(int i = 0; i < m; ++i) // 把剩下的O全修改成X，R全修改成O
        {
            for(int j = 0; j < n; ++j)
            {
                if(board[i][j] == 'O')
                    board[i][j] = 'X';
                else if(board[i][j] == 'R')
                    board[i][j] = 'O';
            }
        }
    }

    void bfs(vector<vector<char>>& board, int i, int j)
    {
        queue<pair<int, int>> q;
        q.push({i, j});
        board[i][j] = 'R';
        while(!q.empty())
        {
            auto [a, b] = q.front();
            q.pop();
            for(int i = 0; i < 4;  ++i)
            {
                int x = a + dx[i], y = b + dy[i];
                if(x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'O')
                {
                    q.push({x, y});
                    board[x][y] = 'R';
                }
            }
        }
    }
};