前言

笔者最近在研究如何又简单又精准的对微信小程序进行HTTP/HTTPS流量抓包，然后进行渗透测试。研究了几天，发现了一个最适合自己的方法，特此进行记录。

前期准备

• 流量工具：Proxifier
• 抓包工具：BurpSuite
• 电脑端微信：安装版/绿色版都可以

思维流程

思维流程图

正式教程

一、启动微信

• 登录上你的电脑微信，随便打开一个小程序
• 打开Windows任务管理器(Ctrl+Shift+ESC)，看到有WeChatAppEx.exe进程即可。

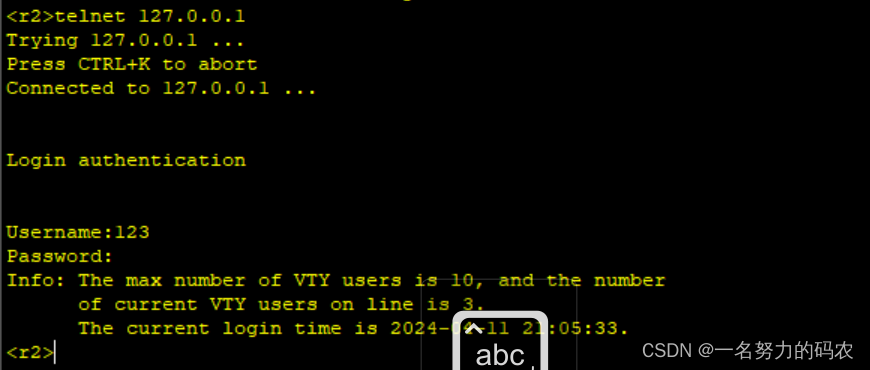
二、启动BurpSuite

• 启动BurpSuite，并且安装了BurpSuite的证书（抓HTTPS数据包用）。如果没有BurpSuite可以去本站下载，不会安装BurpSuite证书的话可以去百度一下！
• 将监听端口设置为默认8080端口（任意都行，不懂就按本教程来）

三、启动Proxifier

• 在Proxifier界面打开代理规则，将如图两个默认规则改为Direct(直连)，防止产生其他软件的数据包。

• 添加代理服务器：代理服务器 -> 添加 -> 填写如图数据 -> 确定保存

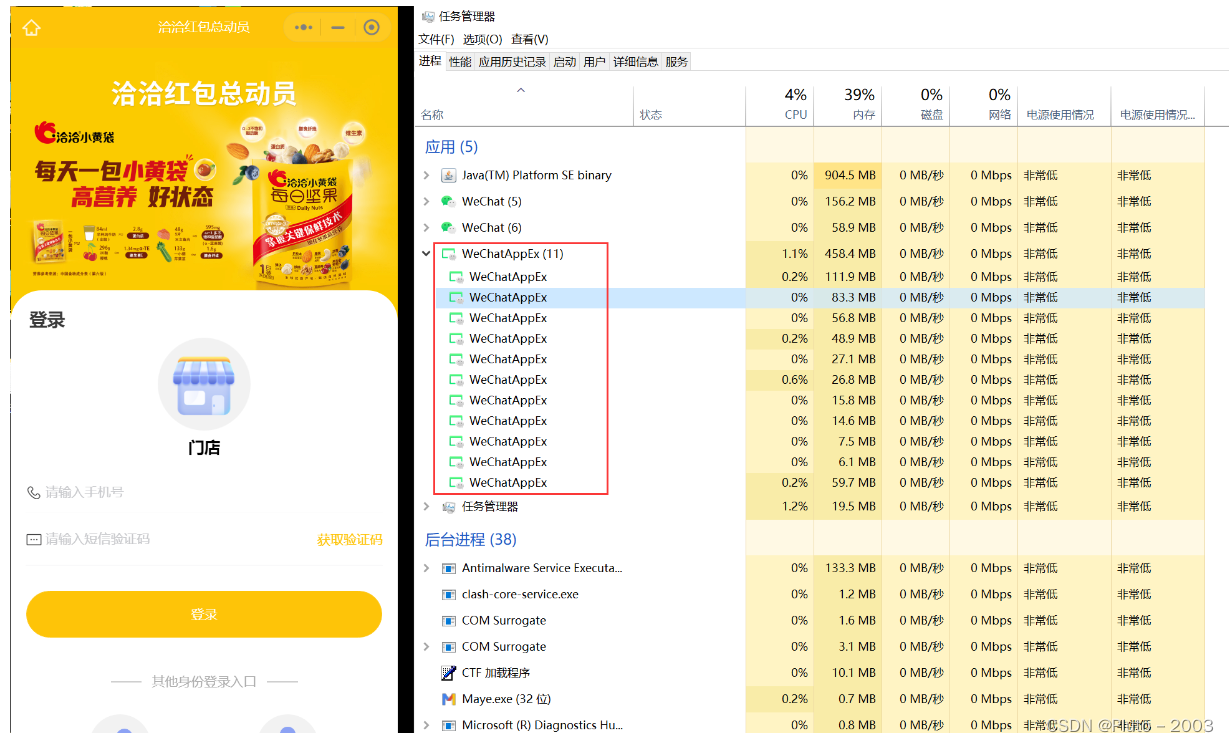
• 添加代理规则，将微信小程序的HTTP数据包进行代理
  • 通过任务管理器找到微信小程序的进程，然后找到EXE文件位置，复制下来

    

  • 添加代理规则：代理规则 -> 添加 -> 应用程序 -> 选择微信小程序的EXE -> 动作选择Proxy HTTPS 127.0.0.1

四、完成

上述操作没问题的话，就可以通过BurpSuite进行抓包了！

 转自：【抓包教程】微信小程序精准流量抓包教程 - 极核GetShell (get-shell.com)