组合数学＜1＞——组合数学基础

news2025/2/24 16:27:09

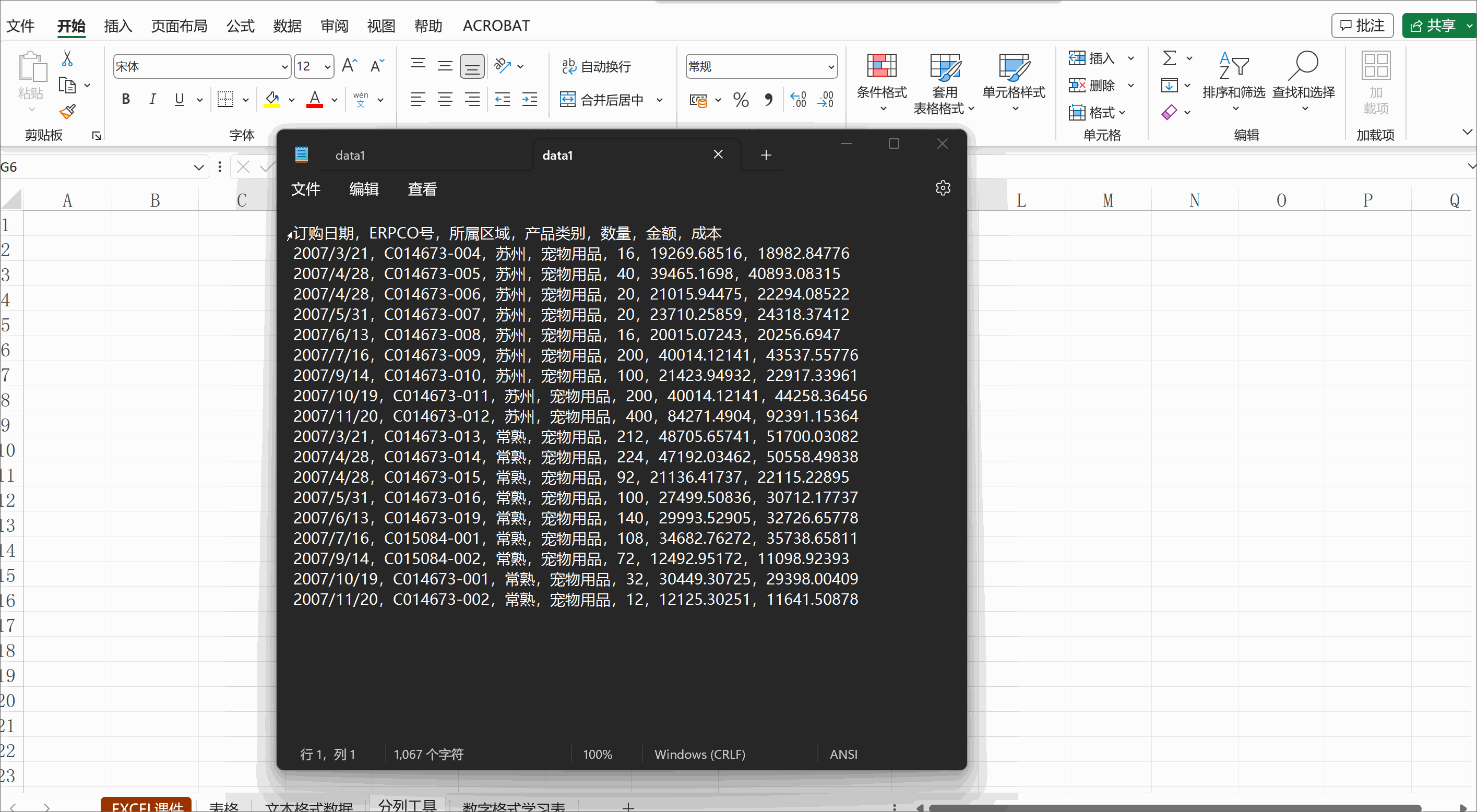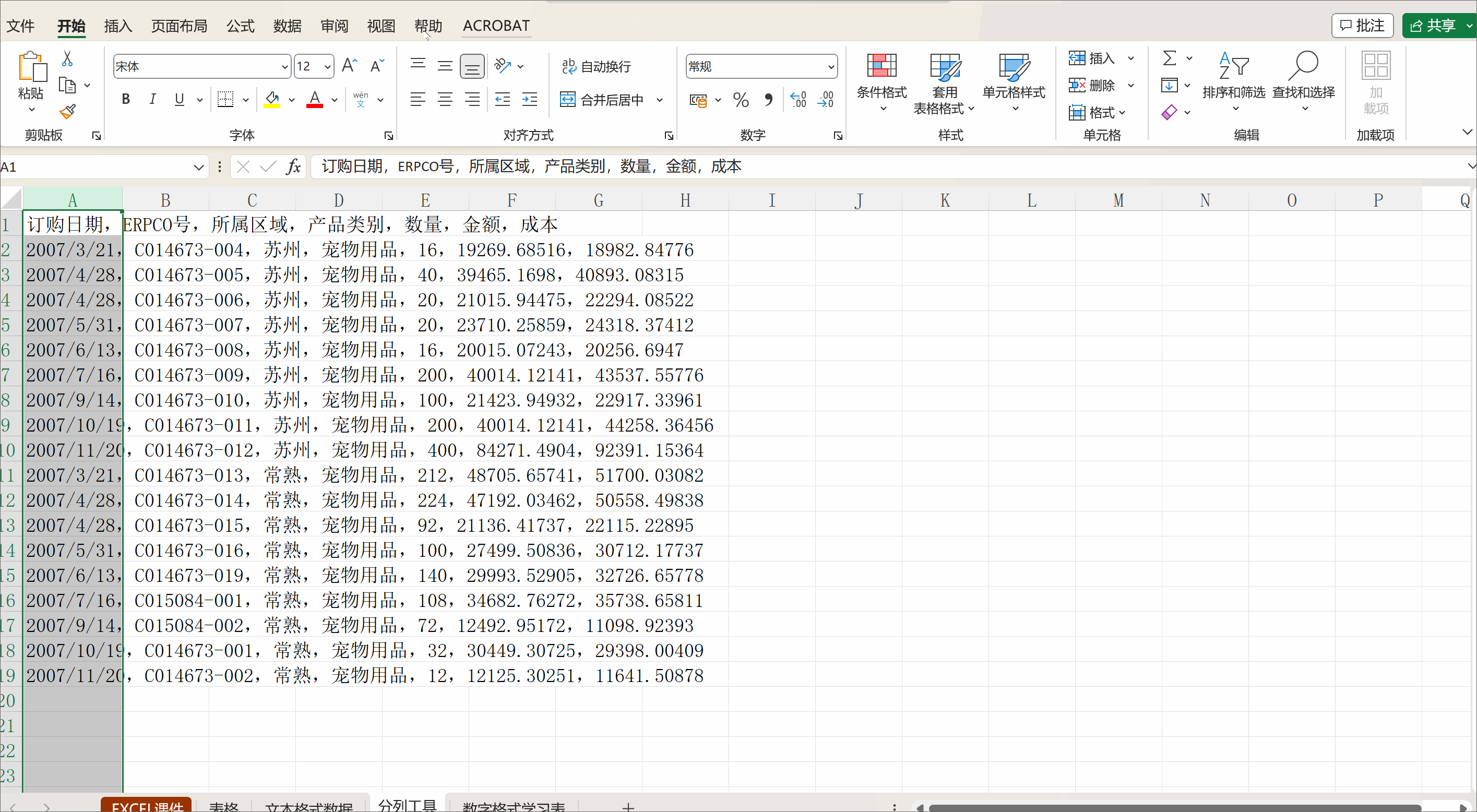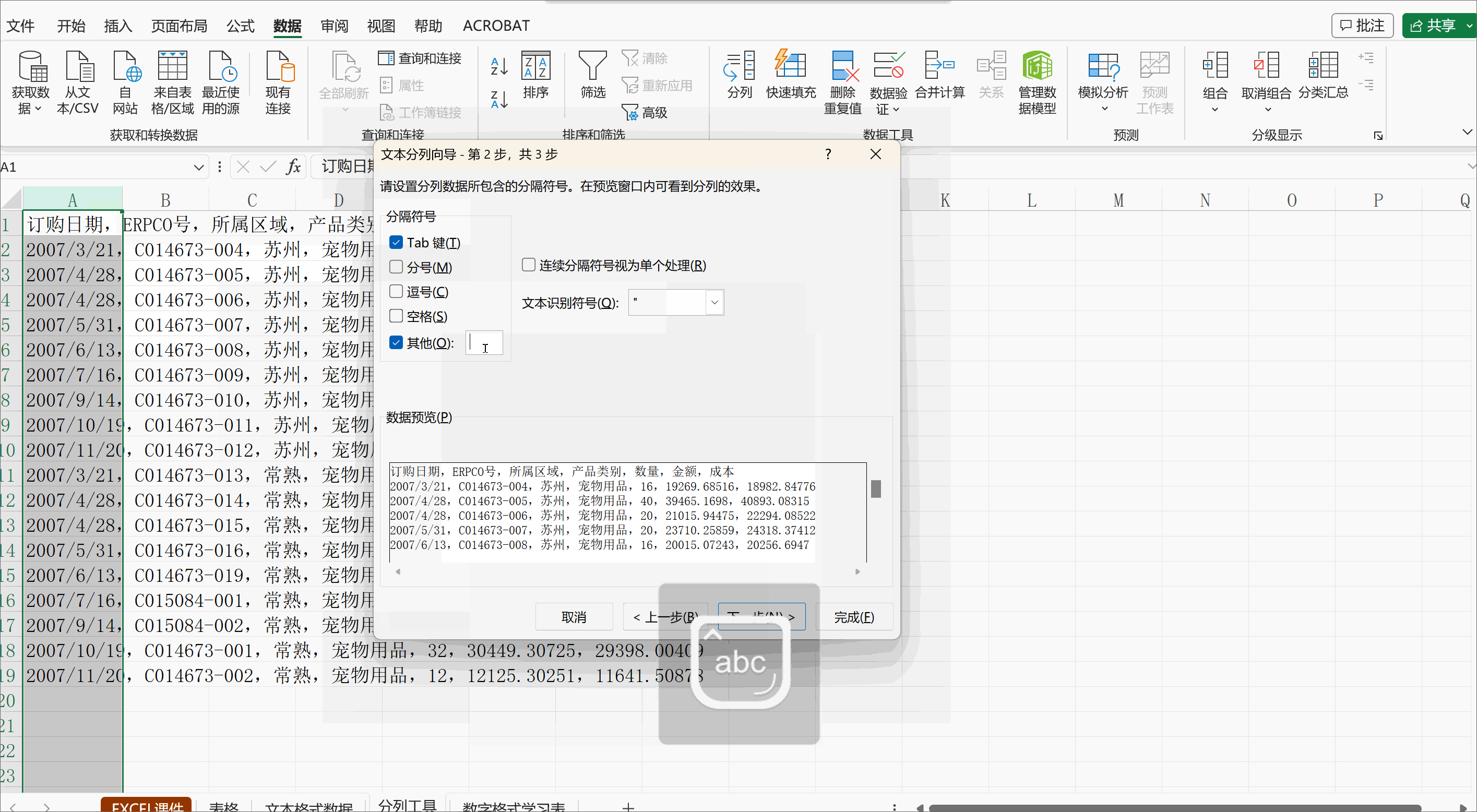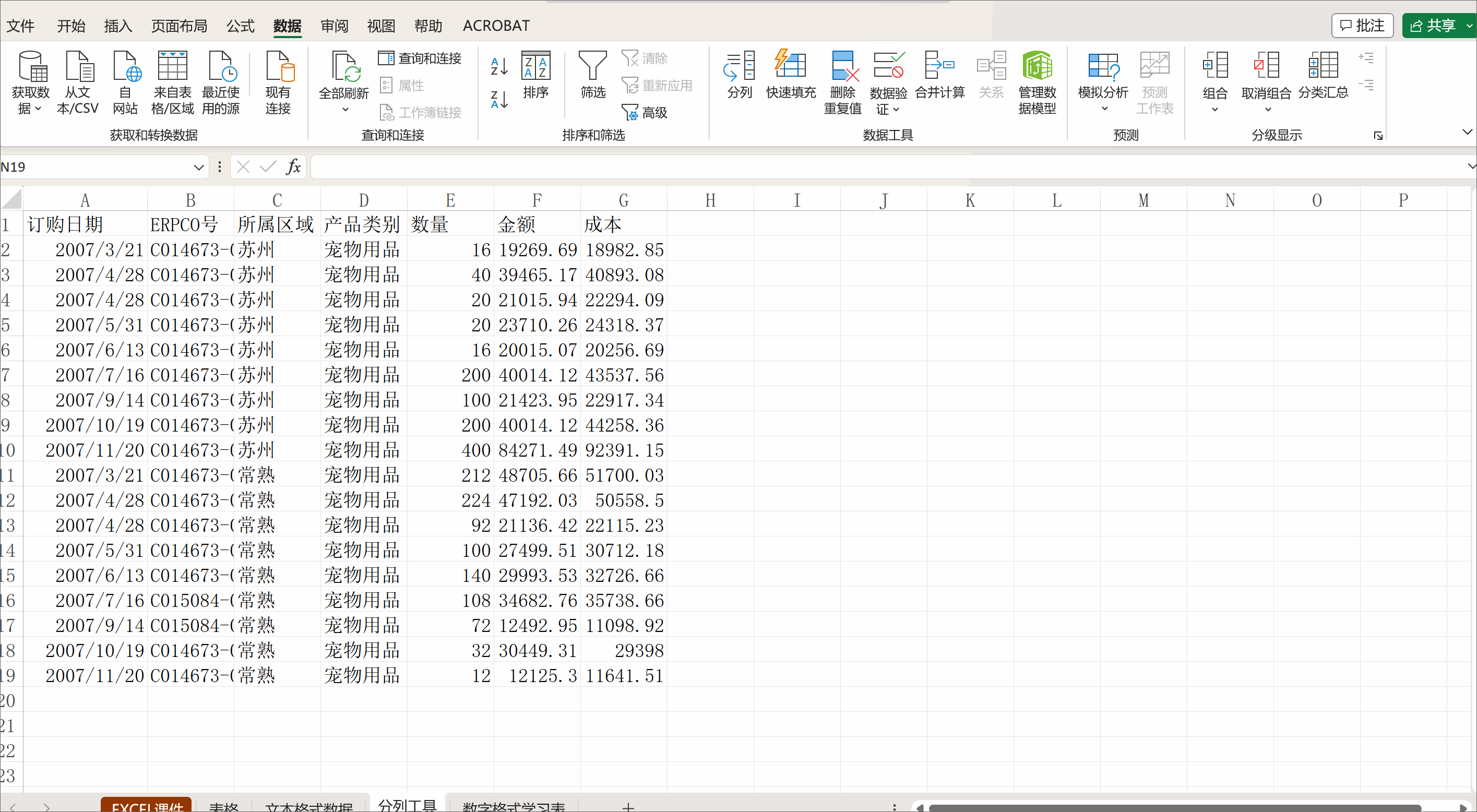
今天我们聊聊组合数学。(本期是给刚刚学习组合数学的同学看的，dalao们可以自行忽略)

建议:不会求逆元的出门左转数论<2>，不会数论的出门右转数论<1>。

加乘原理

加乘原理小学奥数就有。

总的来说:加法原理:分类;乘法原理:分步

比如说，我问你有3条裤子2件衣服，只买一个，有几种可能性？3+2对吧。

那还是3条裤子2件衣服，每个买一个，有几种？3*2对吧。

排列组合

排列组合也是小学奥数的东西。

举个栗子，n个学生，选m个出来排队，有几种方案？ $A(n,m)$ ！

稍微解释一下 $A(n,m)=n\times (n-1)\times (n-2)\times (n-m+1)......=\frac{n!}{(n-m)!}$ 。

那还是刚刚的问题，但是不考虑排队的顺序，有几种方案？ $C(n,m)$ ！

由于不考虑方案，所以要在 $A(n,m)$ 的基础上除 $m!$ ，也就是 $C(n,m)=\frac{n!}{m!(n-m)!}$ 。

圆排列

有N个人围成一个圈，圈可以顺时针旋转，问有多少种方案？

其实很简单。不考虑圈是 $n!$ ，考虑了是 $(n-1)!$ ，也就是除掉一个N。

隔板法

原型: $x_1+x_2+......+x_n=m\: (x_i>1)$ ，问有多少种方案。

在 $x_i$ 旁边放隔板，有 $n-1$ 个隔板，所以答案是 $C(m-1,n-1)$

变形1: $x_1+x_2+......+x_n=m$ ， $x_i$ 可以是 $0$ ，问方案数。

把每个 $x_i$ 加1，也就是 $(x_1+1)+(x_2+1)+......+(x_n+1)=m+n\: (x_i\geq 1)$ 。

答案是 $C(m+n-1,n-1)$ 。

变形2: $1\leq x_1< x_2 <...... <x_n\leq m$ ，求方案数。

$(x_1-1+1)+(x_2-x_1)+......(x_n-x_{n-1}+1)=m+1$ ，答案为 $C(m,n)$ ！！！

变形3: $A_1\times A_2\times A_3\times ......A_N=M$ ，求方案数。

我们知道， $M=p_1^{\alpha_1}+p_2^{\alpha_2}+......+p_k^{\alpha_k}$ ，而每个 $A_i$ 的分解质因数都在 $M$ 里，就得到

$\beta_{1,1}+\beta_{1,2}+......+\beta_{1,N}=\alpha_1$ ，然后就转化为原型。( $\beta$ 是每个数的指数)

-----------------------------------------↑数学-------↓实现-----------------------------------------

求组合数

首先可以想到的是根据定义操作。

int C(int n,int m){
	int res=1;
	for(int i=m-n+1;i<=m;i++)
		res=res*i/(i-m+n);
	return res;
}

我这里稍微优化了一下，边乘边除，防止溢出。

取模组合数

有的题ans太大了，需要大家取模。但是在数论<2>中我们说过，这除法有鬼啊，模不了，不能只

接求，那怎么办呢？

杨辉三角递推

观察杨辉三角，你会发现，杨辉三角的 $(i,j)$ 就是 $C(i,j)$ 的值。(竖过来看)

而且，还满足 $C(i,j)=C(i-1,j-1)+C(i-1,j)$ ，因此就可以 $\Theta (n^2)$ 求组合数了。

而且这是加法，很好模。当然，它只适用于 $n$ 和 $m$ 较小的情况。

逆元

或许大家有疑问，我们能不能搞个前缀积，然后 $C(n,m)=prod(n)/prod(m)/prod(n-m)$

还搞什么杨辉三角呢？有道理，但是我们知道，除法并不支持模运算(⊙︿⊙)

所以，我们可以用逆元。逆元怎么求在数论<2>中说过，这里不再赘述。

然后，根据上面的式子就可以求逆元啦！

long long factorial[maxn],invf[maxn];
long long exgcd(long long a,long long b,long long &x,long long &y){
	if(b==0){
		x=1;
		y=0;
		return a;
	}
	long long res=exgcd(b,a%b,x,y);
	long long tmp=x;
	x=y;
	y=tmp-a/b*y;
	return res;
}
long long inverse(long long n,long long mod){
	long long x,y;
	long long _=exgcd(n,mod,x,y);
	x%=mod;
	if(x<0)
		x+=mod;
	return x;
}
void precompute(){
	factorial[0]=1;
	for(int i=1;i<=maxn;i++)
		factorial[i]=factorial[i-1]*i%P;
	invf[maxn]=inverse(factorial[maxn],P);
	for(int i=maxn-1;i>=0;i--)
		invf[i]=invf[i+1]*(i+1)%P;
}
long long C(int n,int m){
	long long res=factorial[n];
	res=res*invf[n-m]%P;
	res=res*invf[m]%P;
	return res;
}

都开了long long，因为组合数学题的范围一般很大。

例题

CF630F:

很easy， $C(n,5)+C(n,6)+C(n,7)$ 就搞定了。边乘边除即可。