easy_crypto

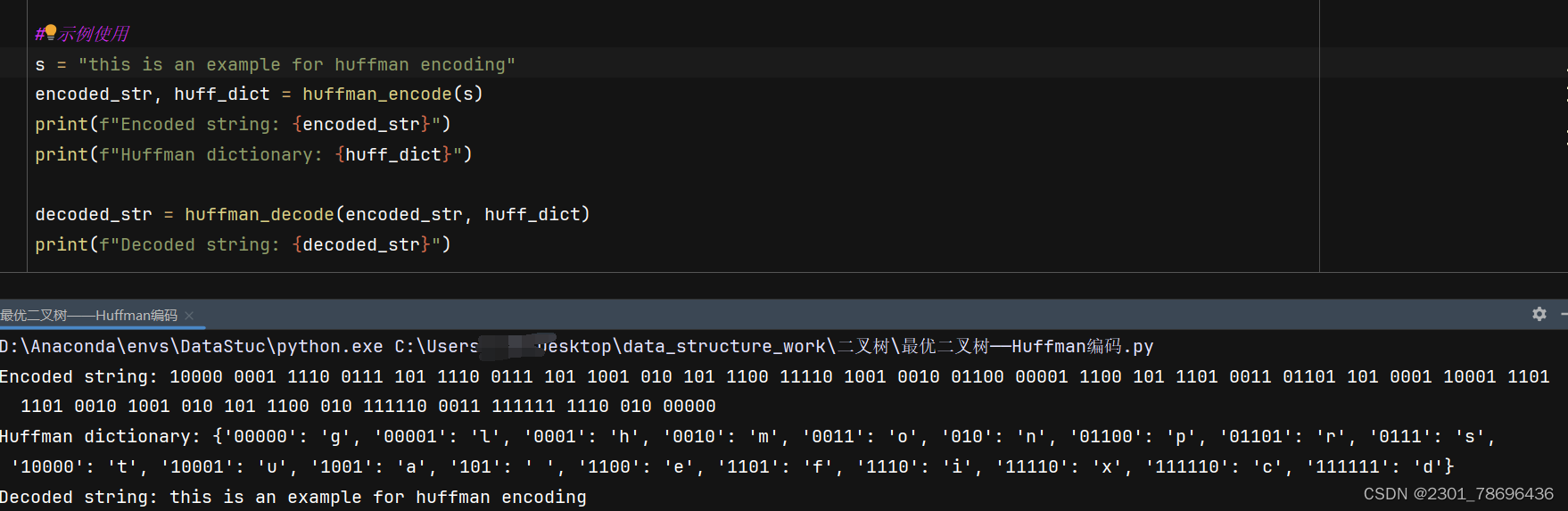
附件easy_crypto.txt，内容是社会核心主义观

公正公正公正诚信文明公正民主公正法治法治诚信民主自由敬业公正友善公正平等平等法治民主平等平等和谐敬业自由诚信平等和谐平等公正法治法治平等平等爱国和谐公正平等敬业公正敬业自由敬业平等自由法治和谐平等文明自由诚信自由平等富强公正敬业平等民主公正诚信和谐公正文明公正爱国自由诚信自由平等文明公正诚信富强自由法治法治平等平等自由平等富强法治诚信和谐

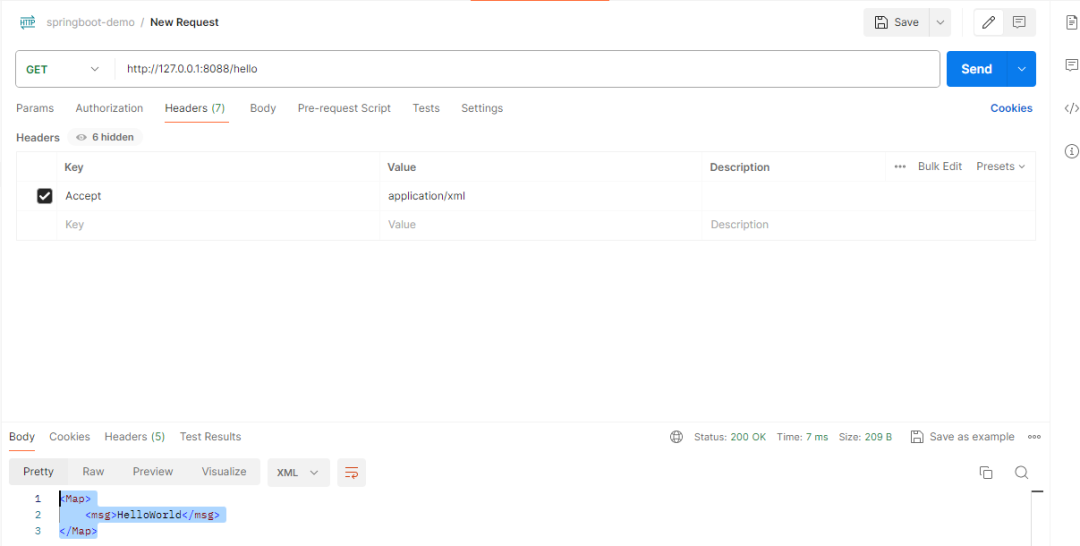
使用工具解密

flag{IlUqU9O5guX6YiITsRNPiQmbhNRjGuTP}

A_CRYPTO

题目描述为：

4O595954494Q32515046324757595N534R52415653334357474R4N575955544R4O5N4Q46434S4O59474253464Q5N444R4Q51334557524O5N4S424944473542554O595N44534O324R49565746515532464O49345649564O464R4R494543504N35

使用ciphey解密：

flag{W0w_y0u_c4n_rea11y_enc0d1ng!}

BabyRSA

附件内容包括：
out.txt:

1514296530850131082973956029074258536069144071110652176122006763622293335057110441067910479
40812438243894343296354573724131194431453023461572200856406939246297219541329623
21815431662065695412834116602474344081782093119269423403335882867255834302242945742413692949886248581138784199165404321893594820375775454774521554409598568793217997859258282700084148322905405227238617443766062207618899209593375881728671746850745598576485323702483634599597393910908142659231071532803602701147251570567032402848145462183405098097523810358199597631612616833723150146418889589492395974359466777040500971885443881359700735149623177757865032984744576285054725506299888069904106805731600019058631951255795316571242969336763938805465676269140733371287244624066632153110685509892188900004952700111937292221969
19073695285772829730103928222962723784199491145730661021332365516942301513989932980896145664842527253998170902799883262567366661277268801440634319694884564820420852947935710798269700777126717746701065483129644585829522353341718916661536894041337878440111845645200627940640539279744348235772441988748977191513786620459922039153862250137904894008551515928486867493608757307981955335488977402307933930592035163126858060189156114410872337004784951228340994743202032248681976932591575016798640429231399974090325134545852080425047146251781339862753527319093938929691759486362536986249207187765947926921267520150073408188188

task.py：

from Crypto.Util.number import getPrime, bytes_to_long
from secret import flag

p = getPrime(1024)
q = getPrime(1024)
n = p * q
e = 65537
hint1 = p >> 724
hint2 = q % (2 ** 265)
ct = pow(bytes_to_long(flag), e, n)
print(hint1)
print(hint2)
print(n)
print(ct)

hint1 = p >> 724 ：表示对整数p执行右移位操作，hint1是p除以 2^724 ，$hint1\ast 2^{724}=p$
hint2 = q % (2 ** 265)：表示对整数q执行取模运算，hint2是q除以 2^265 后取余数，$hint2=q\%(2^{265})$

令p1=hint1作为p的高位(300位)
令q0 = hint2作为q取模的结果，则$q_0=q\%(2^{265})$
=> $q=q_0+2^{265}k$
=> $n=p{q}_0+2^{265}kp$
=> $n{q}_0^{-1}=p+2^{265}kp{q}_0^{-1}$
=> $p_0=n{q}_0^{-1}\%(2^{265})$

#sage
p1 = 1514296530850131082973956029074258536069144071110652176122006763622293335057110441067910479
q0 = 40812438243894343296354573724131194431453023461572200856406939246297219541329623
n = 21815431662065695412834116602474344081782093119269423403335882867255834302242945742413692949886248581138784199165404321893594820375775454774521554409598568793217997859258282700084148322905405227238617443766062207618899209593375881728671746850745598576485323702483634599597393910908142659231071532803602701147251570567032402848145462183405098097523810358199597631612616833723150146418889589492395974359466777040500971885443881359700735149623177757865032984744576285054725506299888069904106805731600019058631951255795316571242969336763938805465676269140733371287244624066632153110685509892188900004952700111937292221969

p0=n*invert(q0,2^265)%(2^265)
pbar=(p1<<724)+p0

PR.<x> = PolynomialRing(Zmod(n))
 
for i in range(32):
    f=pbar+x*(2^265)*32
    f=f.monic()
    pp=f.small_roots(X=2^454,beta=0.4)
    if(pp):
        break
    pbar+=2^265
 
p=pbar+pp[0]*32*(2^265)
assert n%p==0
print("p=",p)

#python
from gmpy2 import *
from Crypto.Util.number import *
 
n = 21815431662065695412834116602474344081782093119269423403335882867255834302242945742413692949886248581138784199165404321893594820375775454774521554409598568793217997859258282700084148322905405227238617443766062207618899209593375881728671746850745598576485323702483634599597393910908142659231071532803602701147251570567032402848145462183405098097523810358199597631612616833723150146418889589492395974359466777040500971885443881359700735149623177757865032984744576285054725506299888069904106805731600019058631951255795316571242969336763938805465676269140733371287244624066632153110685509892188900004952700111937292221969
c=19073695285772829730103928222962723784199491145730661021332365516942301513989932980896145664842527253998170902799883262567366661277268801440634319694884564820420852947935710798269700777126717746701065483129644585829522353341718916661536894041337878440111845645200627940640539279744348235772441988748977191513786620459922039153862250137904894008551515928486867493608757307981955335488977402307933930592035163126858060189156114410872337004784951228340994743202032248681976932591575016798640429231399974090325134545852080425047146251781339862753527319093938929691759486362536986249207187765947926921267520150073408188188
e=65537

#sage计算p
p = 133637329398256221348922087205912367118213472434713498908220867690672019569057789598459580146410501473689139466275052698529257254973211963162087316149628000798221014338373126500646873612341158676084318494058522014519669302359038980726479317742766438142835169562422371156257894374341629012755597863752154328407

q=n//p
phi=(p-1)*(q-1)
d=invert(e,phi)
m=pow(c,d,n)
print(long_to_bytes(m))
#flag{ef5e1582-8116-4f61-b458-f793dc03f2ff}