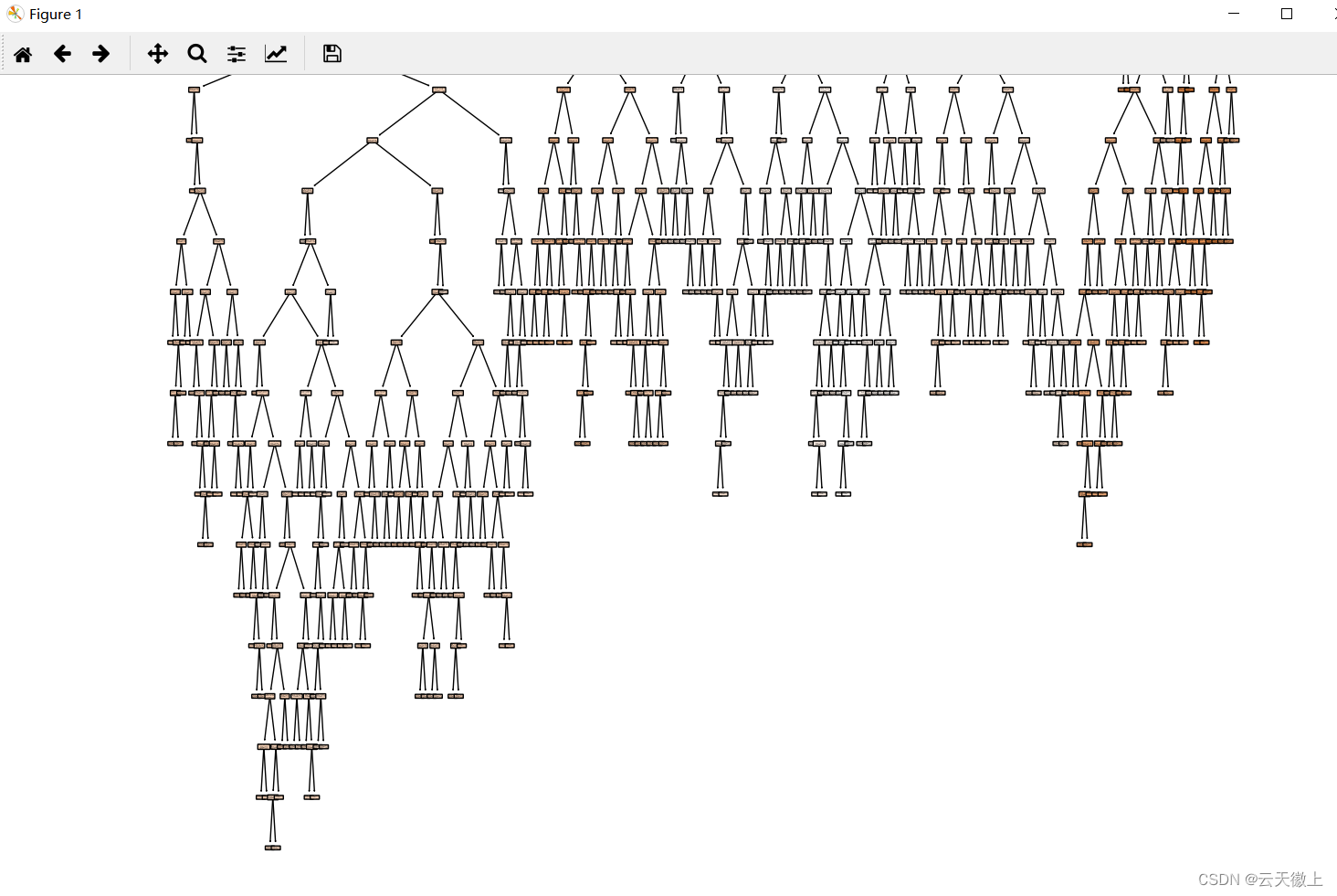
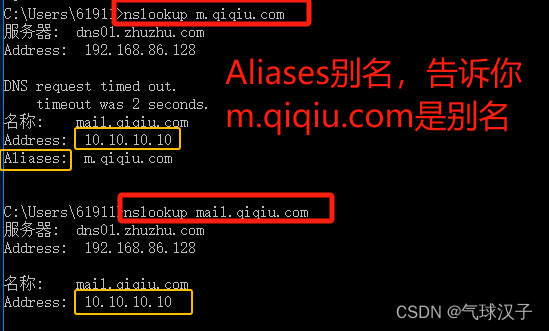
1、外部带权外部路径长度、Huffman树
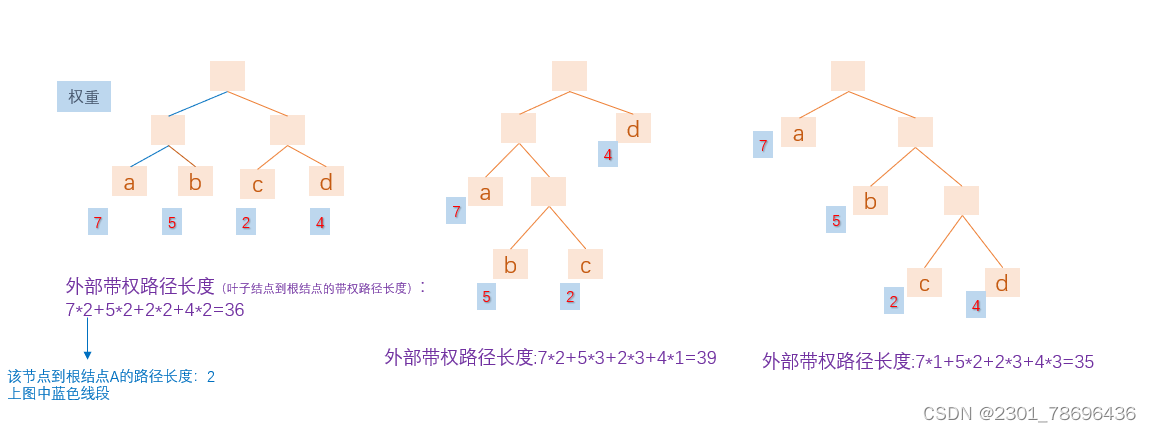
从图中可以看出,深度越浅的叶子结点权重越大,深度越深的叶子结点权重越小的话,得出的带权外部路径长度越小。
Huffman树就是使得外部带权路径最小的二叉树
2、如何构造Huffman树
(1)步骤
(1)根据给定的n个权值{W1,W2,…,Wn},构造n棵二叉树的集合F={T1,T2,…,Tn},其中每棵二叉树中均只含有一个带权值为Wi的根结点,其左右子树为空树
(2)在F中选取其根结点的权值为最小的两棵二叉树,分别作为左、右子树构造一棵新的二叉树,并置这棵新的二叉树根结点的权值为其左、右子树根结点的权值之和;
(3)从F中删去这两棵树,同时加入刚生成的新树;
(4)重复(2)和(3)两步,直至F中只含一棵树为止
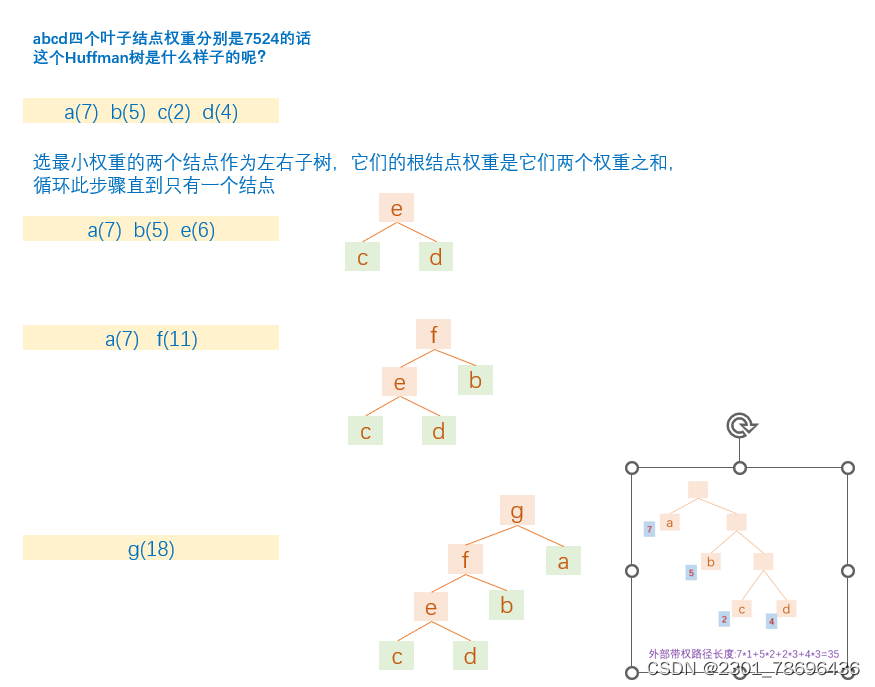
以上图的结点为例:
(2)代码
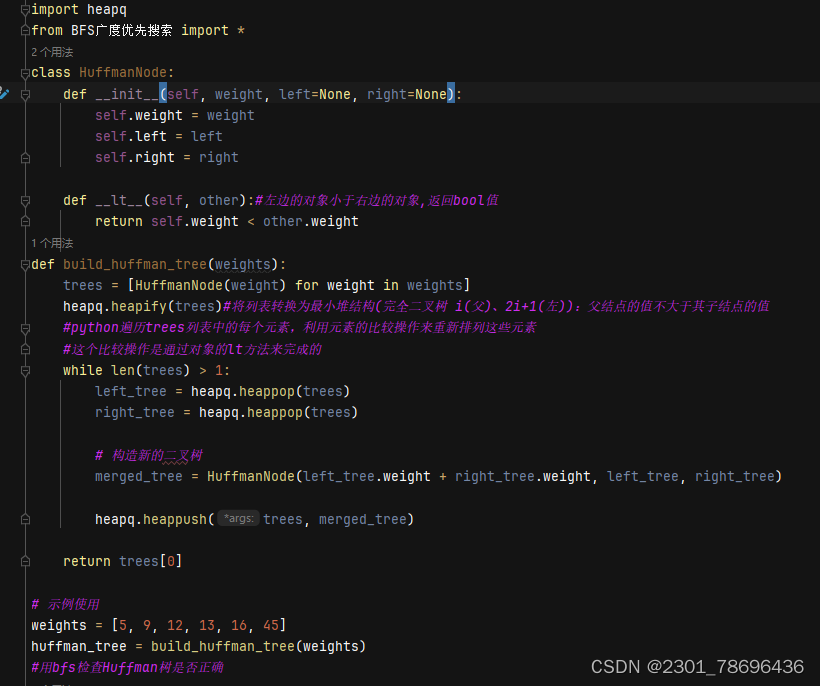
用bfs广度优先搜索遍历这个二叉树来检验
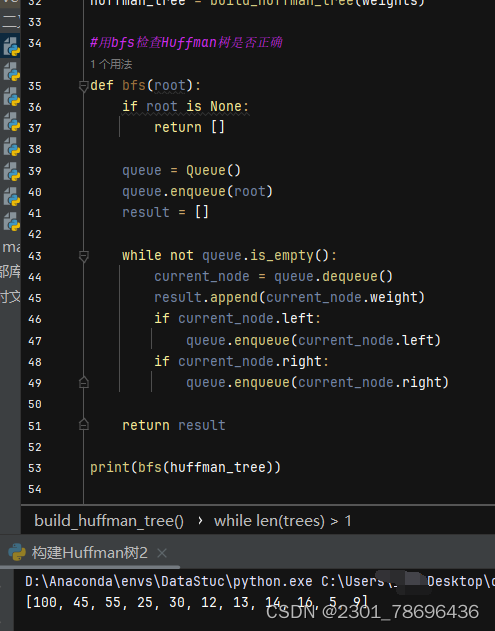
(3)代码注意点
2、ASCII码
在ASCII(American Standard Code for Information Interchange,美国信息交换标准代码)编码中,每个大写或小写英文字母都被赋予一个唯一的数字值。这些值都是7位的二进制数,但在实际存储和传输时,它们通常会被填充为一个字节(8位),最高位(第8位)设置为0。
对于小写字母 ‘a’,其ASCII码值是97(十进制)。在二进制表示中,它是 01100001。
同理,大写字母 ‘A’ 的ASCII码值是65(十进制),二进制表示为 01000001。
请注意,ASCII码只包含128个字符,包括大小写英文字母、数字、标点符号和一些控制字符。如果需要表示更多的字符,比如各种语言的文字符号,就需要使用扩展的字符编码,如ISO 8859系列、Unicode等。
3、Huffman编码
哈夫曼编码,它是一种可变长编码方式,根据字符出现频率来构造异字头的平均长度最短的码字,是数据压缩算法中的一种。哈夫曼编码是贪婪算法的应用之一。哈夫曼树又称最优二叉树,带权路径长度最短的二叉树。所谓树的带权路径长度,就是树中所有的叶结点的权值乘上其到根结点的路径长度(若根结点为0层,叶结点到根结点的路径长度为叶结点的层数)。树的带权路径长度记为WPL=(W1L1+W2L2+W3L3+…+WnLn),N个权值Wi(i=1,2,…n)构成一棵有N个叶结点的二叉树,相应的叶结点的路径长度为Li(i=1,2,…n)。可以证明哈夫曼树是WPL最小的二叉树,故有时也称哈夫曼编码为最优前缀码。
(1)Huffman编码对比其他编码方式的优势
这里先给出一个字符串:"this is isinglass’’
其中共有15个字符。
假如用ASCII码编码,ASCII编码每个字符用7个二进制数,但在存储时会被填充成一个字节,即8位,因此占位:15*8=120
在ASCII码的基础上进行改进,每个字符用3位表示,占位:15*3=45
我们再来看一下Huffman编码
文字部分可以打开图片直接对照,也可以先看文字解释

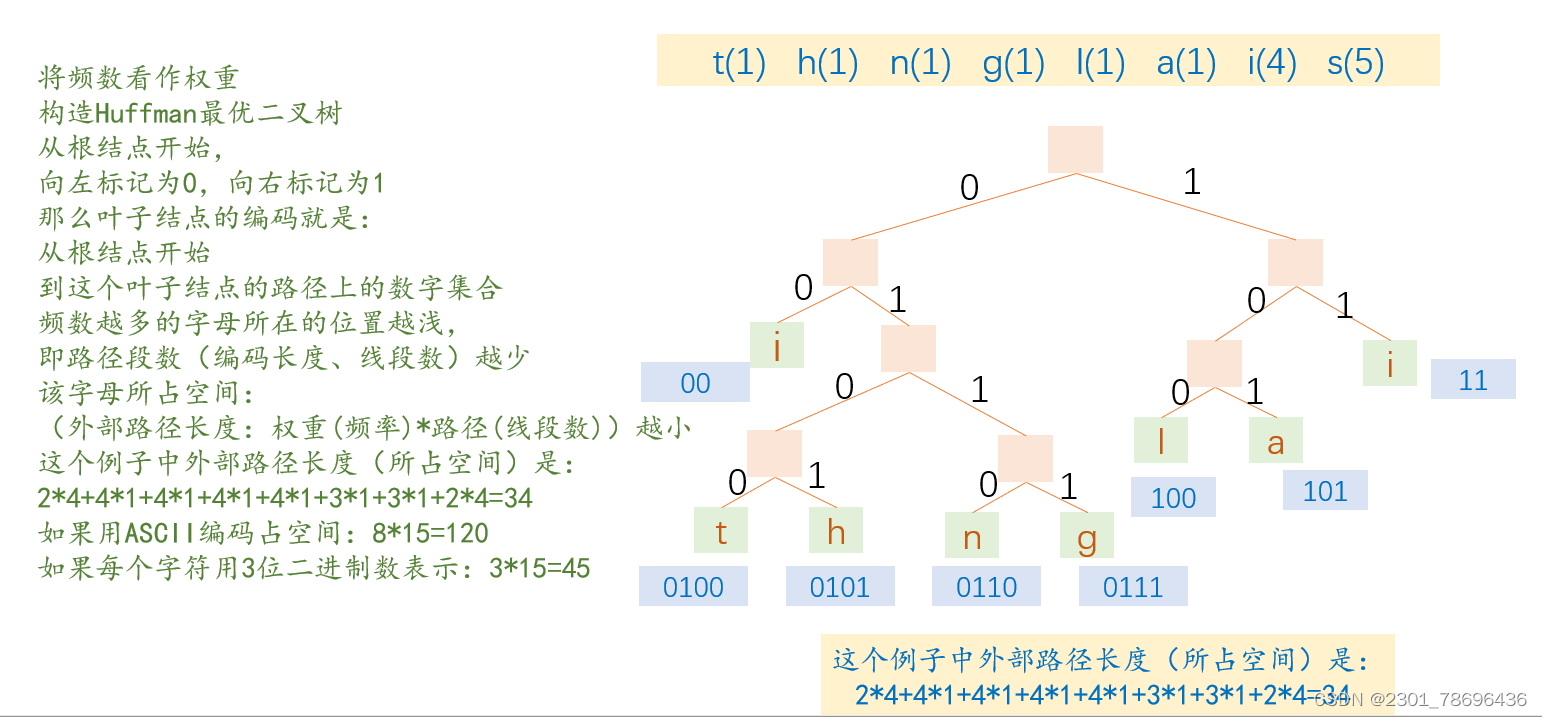
经过上述对比可以很明显看出Huffman编码的好处
(2)Huffman编码具有前缀特性
思考:为什么不给频率最高的字母s和i以最短的编号,如分别是0、1,然后剩余编号:00,01,10,11,000,001?这样不就能最大程度节省空间了吗?
其实这样是不正确的 。
首先,我们需要理解Huffman编码的目标:它是为了创建一种前缀编码(prefix code),在这种编码中,任何字符的编码都不是其他字符编码的前缀。这意味着编码字符串可以无歧义地解码回原始字符序列。如果我们简单地给频率最高的字母分配最短的编码(如0或1),那么很可能会有多个字符的编码成为其他字符编码的前缀,从而违反了前缀编码的原则。(解码时会出现二异性)
其次,Huffman编码追求的是整体编码长度的最小化,而不仅仅是单个字符编码长度的最小化。通过将频率最低的字符分配最长的编码,而频率最高的字符分配最短的编码,Huffman编码确保了整体编码长度最短。这是基于信息论中的最优编码理论,即使用最少的位数来表示最可能出现的事件。
Huffman树的前缀特性是由其构建过程自然产生的。Huffman树的构建过程确保了每个字符的编码都是唯一的,并且没有一个是另一个的前缀。这是因为Huffman树是一个二叉树,每个字符都是树的一个叶子节点,从根节点到该叶子节点的路径决定了该字符的编码。由于树的结构保证了从根到每个叶子节点的路径是唯一的,因此每个字符的编码也是唯一的,并且没有前缀冲突。
最后,虽然将频率最高的字母的编码设置为0和1可能在某些情况下看似节省空间,但这并不适用于所有情况。Huffman编码是一种通用的、自适应的编码方法,它根据字符的实际频率分布来构建编码,从而在各种不同的情况下都能达到较好的压缩效果。而简单地给某个字符分配固定的短编码可能会在某些特定情况下导致较差的压缩性能。
综上所述,Huffman编码不直接将频率最高的字母的编码设置为0和1,而是基于Huffman树来构建前缀编码系统,这是为了确保编码的唯一性和无前缀冲突,同时追求整体编码长度的最小化。Huffman树的前缀特性是由其构建过程自然产生的,保证了每个字符的编码都是唯一的。
(2)代码实现
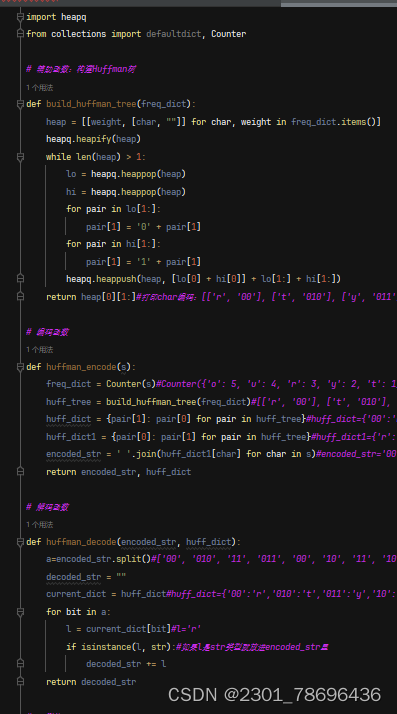
代码拆分理解构
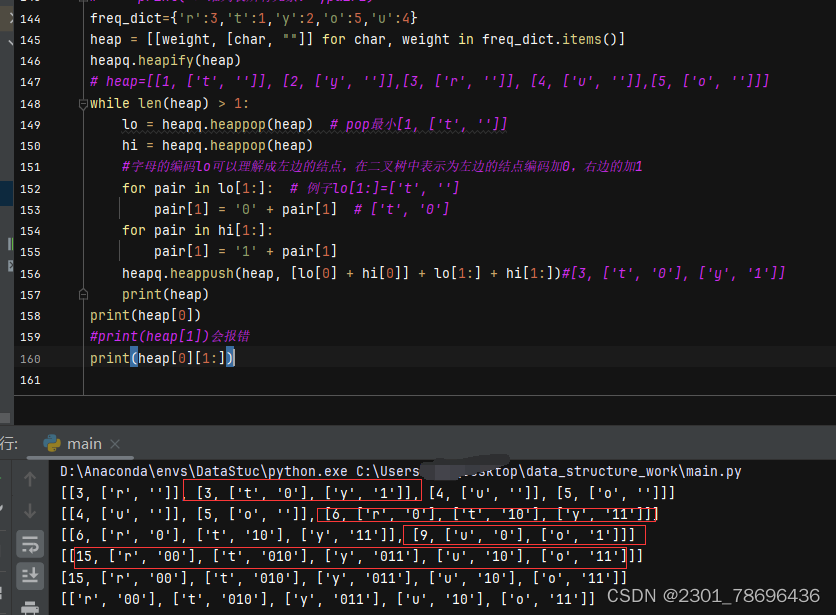
1、构建最优二叉树:
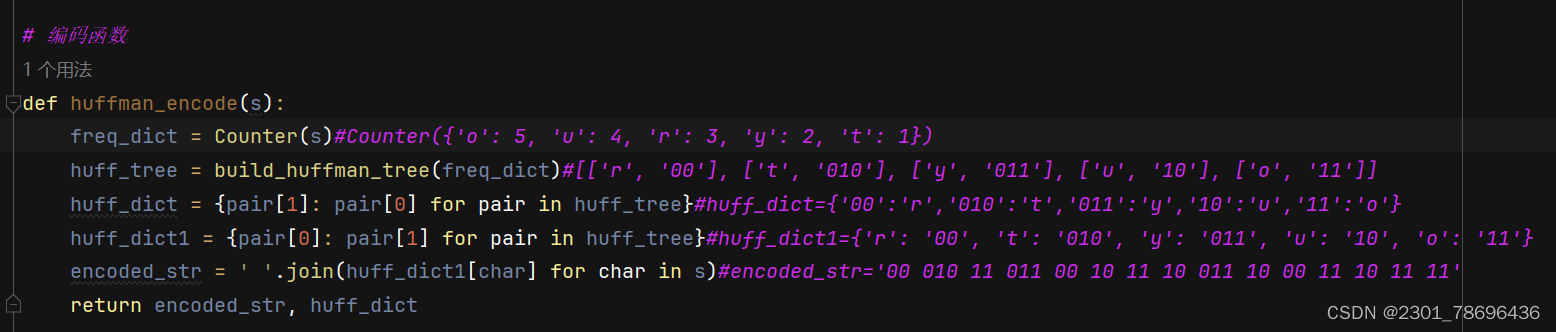
2、编码函数
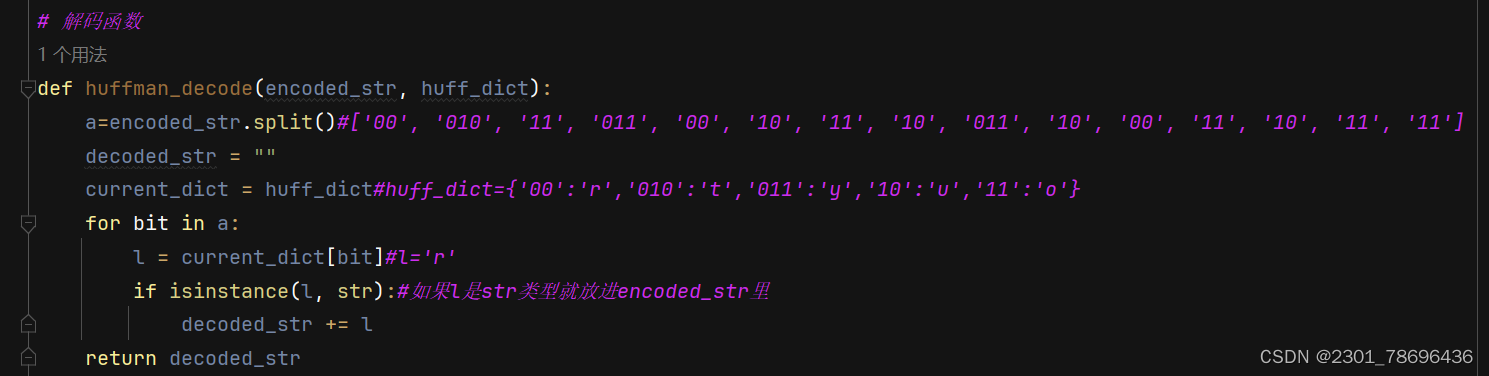
3、解码函数
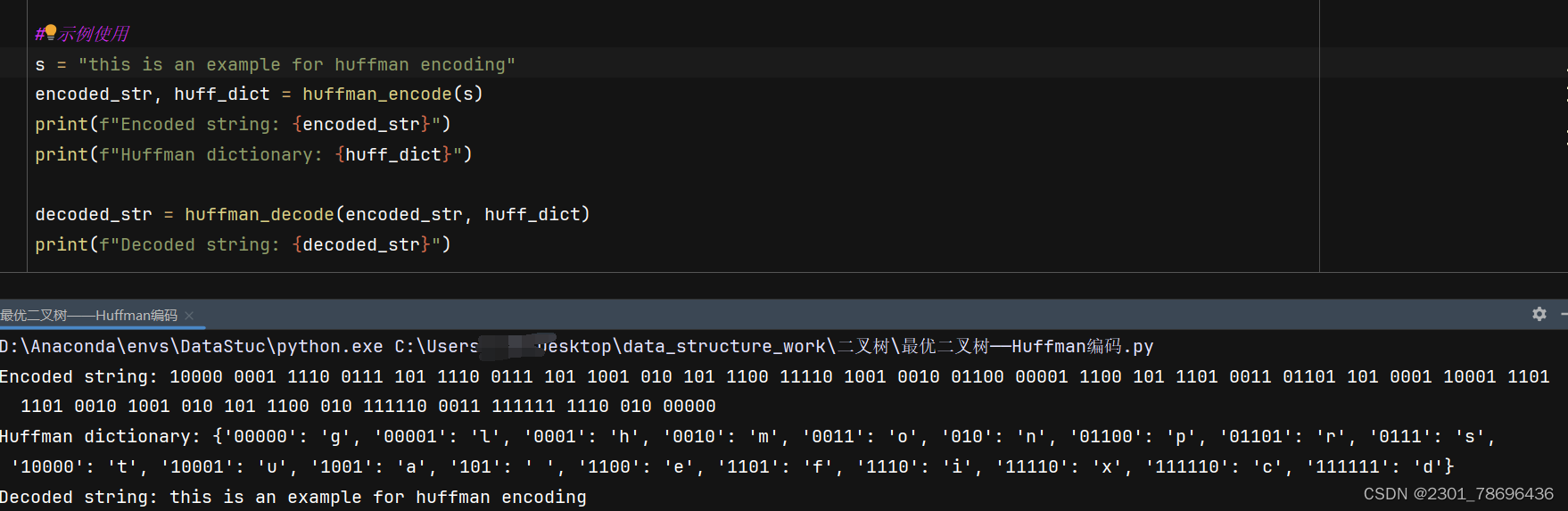
4、实例使用
import heapq
from collections import defaultdict, Counter
# 辅助函数:构建Huffman树
def build_huffman_tree(freq_dict):
heap = [[weight, [char, ""]] for char, weight in freq_dict.items()]
heapq.heapify(heap)
while len(heap) > 1:
lo = heapq.heappop(heap)
hi = heapq.heappop(heap)
for pair in lo[1:]:
pair[1] = '0' + pair[1]
for pair in hi[1:]:
pair[1] = '1' + pair[1]
heapq.heappush(heap, [lo[0] + hi[0]] + lo[1:] + hi[1:])
return heap[0][1:]#打印char编码:[['r', '00'], ['t', '010'], ['y', '011'], ['u', '10'], ['o', '11']]
# 编码函数
def huffman_encode(s):
freq_dict = Counter(s)#Counter({'o': 5, 'u': 4, 'r': 3, 'y': 2, 't': 1})
huff_tree = build_huffman_tree(freq_dict)#[['r', '00'], ['t', '010'], ['y', '011'], ['u', '10'], ['o', '11']]
huff_dict = {pair[1]: pair[0] for pair in huff_tree}#huff_dict={'00':'r','010':'t','011':'y','10':'u','11':'o'}
huff_dict1 = {pair[0]: pair[1] for pair in huff_tree}#huff_dict1={'r': '00', 't': '010', 'y': '011', 'u': '10', 'o': '11'}
encoded_str = ' '.join(huff_dict1[char] for char in s)#encoded_str='00 010 11 011 00 10 11 10 011 10 00 11 10 11 11'
return encoded_str, huff_dict
# 解码函数
def huffman_decode(encoded_str, huff_dict):
a=encoded_str.split()#['00', '010', '11', '011', '00', '10', '11', '10', '011', '10', '00', '11', '10', '11', '11']
decoded_str = ""
current_dict = huff_dict#huff_dict={'00':'r','010':'t','011':'y','10':'u','11':'o'}
for bit in a:
l = current_dict[bit]#l='r'
if isinstance(l, str):#如果l是str类型就放进encoded_str里
decoded_str += l
return decoded_str
# 示例使用
s = "this is an example for huffman encoding"
encoded_str, huff_dict = huffman_encode(s)
print(f"Encoded string: {encoded_str}")
print(f"Huffman dictionary: {huff_dict}")
decoded_str = huffman_decode(encoded_str, huff_dict)
print(f"Decoded string: {decoded_str}")