目录
一.介绍
二.并查集的实现
三路径压缩
四.相关题型
4.1省份数量
一.介绍
什么是并查集?
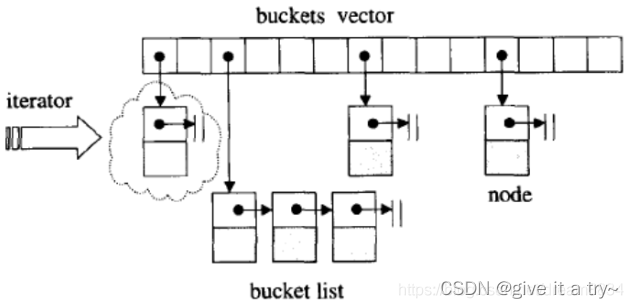
将n个不同的元素划分成一些不相交的集合。开始时,每个元素自成一个 单元素集合,然后按一定的规律将归于同一组元素的集合合并。在这个过程中要反复用到查询某一 个元素归属于哪个集合的运算。适合于描述这类问题的抽象数据类型称为并查集(union-find set)。
例如:

一开始共有0-9,共10个数,将它们的下表初始化为-1,表示这10个数各不相关,都属于不同的集合。现在,将它们开始合并,假设是这样合并:
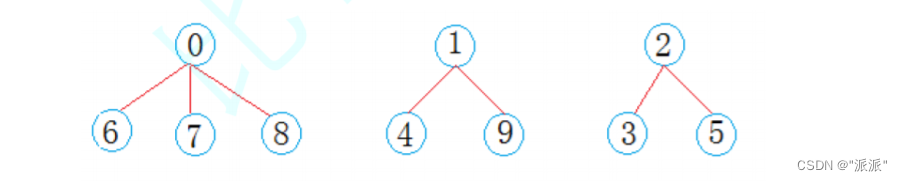

将要合并的两个元素进行如下操作:
1-将要合并的两个元素的值进行相加,将相加的值赋予其中一个元素。
2-将那个未被赋值的元素的值改为那个之前被赋值的元素。
例如:元素0要和元素6进行合并,开始时它们的值都是-1,合并后元素0的值为-2(代表那个集合有两个元素),元素6的值为0,(元素的值不为0,说明它属于某个集合),这里说明元素6属于元素0那个集合。
那么怎么去查找某个元素属于哪个集合,并且知道那个集合的元素个数是多少呢?
例如:
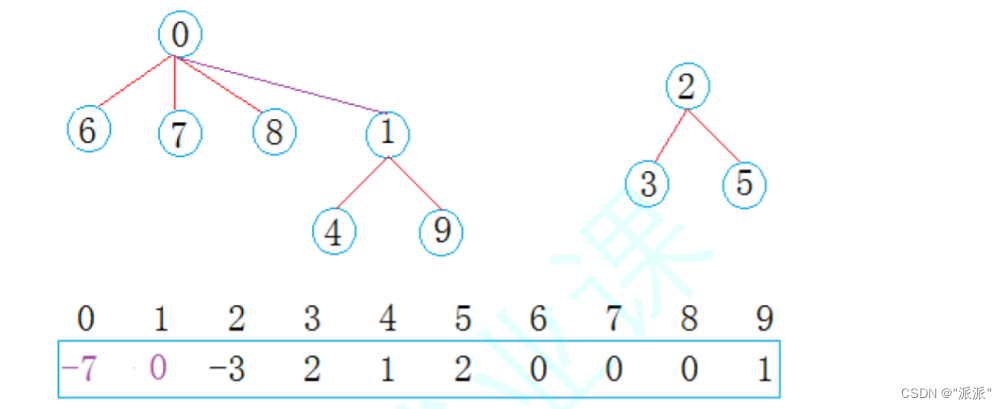
你要查找元素9,9对应的值是1,不是负数,说明元素9属于元素1那个集合,那么再去查找元素1。当查找元素1时,发现它的值是0,也不是负数,说明元素1属于元素0那个集合,那么再去查找元素0。查找元素0时,发现它的值为-7,是负数,说明9属于元素0的集合,集合一共有7个元素。
合并也很简单,分别找到两个元素的根(元素值为负数的),将它们合并即可。
由此可知并查级可以解决的问题:
1. 查找元素属于哪个集合 沿着数组表示树形关系以上一直找到根(即:树中中元素为负数的位置)
2. 查看两个元素是否属于同一个集合 沿着数组表示的树形关系往上一直找到树的根,如果根相同表明在同一个集合,否则不在
3. 将两个集合归并成一个集合 将两个集合中的元素合并 将一个集合名称改成另一个集合的名称
4. 集合的个数 遍历数组,数组中元素为负数的个数即为集合的个数
二.并查集的实现
class UnionFindSet
{
public:
UnionFindSet(int n)
{
_set.resize(n, -1);
}
int find(int x) //查找某个元素属于哪个集合
{
while(_set[x] >= 0)
{
int tmp = _set[x];
x = tmp;
}
return x;
}
void Union(int x, int y)
{
int x = find(x);
int y = find(y);
if (x != y)
{
int sum = _set[x] + _set[y];
_set[x] = sum;
_set[y] = x;
}
}
int SetCount()
{
size_t count = 0;
for (size_t i = 0; i < _set.size(); ++i)
{
if (_set[i] < 0)
count++;
}
return count;
}
private:
vector<int> _set;
};
三路径压缩
查找元素属于哪个集合 沿着数组表示树形关系以上一直找到根(就是值为负数),如果每次都要查找最低层的那些元素,岂不是每次都要去根吗?所以可以每次去更新元素的值,对路劲进行压缩。例如:先找到根,在将那条路径上的依次元素链接到根上
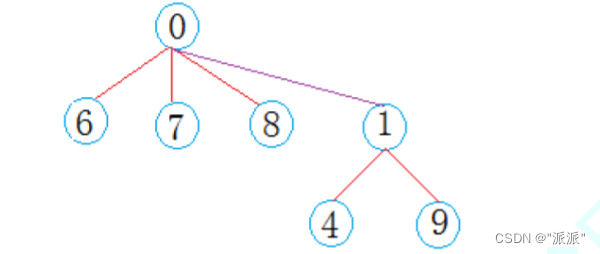
压缩后:

代码实现:
int find(int x) //查找某个元素属于哪个集合
{
int p = x;
while(_set[x] >= 0)
{
int tmp = _set[x];
x = tmp;
}
while (_set[p] >= 0)//路径压缩
{
int tmp = _set[p];
_set[p] = x;
p = tmp;
}
return x;
}四.相关题型
4.1省份数量
题目描述:
有 n 个城市,其中一些彼此相连,另一些没有相连。如果城市 a 与城市 b 直接相连,且城市 b 与城市 c 直接相连,那么城市 a 与城市 c 间接相连。
省份 是一组直接或间接相连的城市,组内不含其他没有相连的城市。
给你一个 n x n 的矩阵 isConnected ,其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连,而 isConnected[i][j] = 0 表示二者不直接相连。
返回矩阵中 省份 的数量。
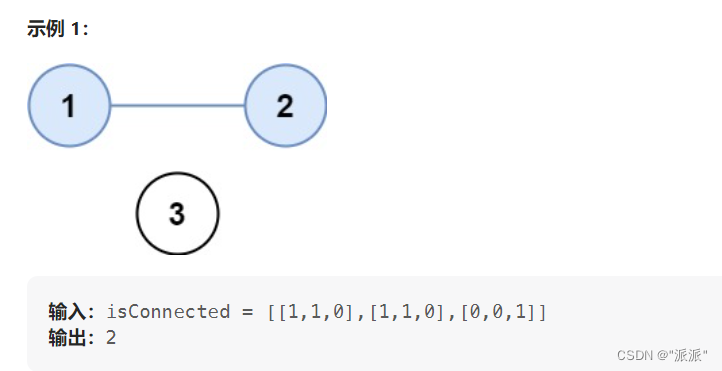
代码示例:
int findCircleNum(vector<vector<int>>& isConnected) {
UnionFindSet U(isConnected.size());
int n=isConnected.size();
for(int i=0;i<n;i++)
{
for(int j=0;j<=i;j++)
{
if(isConnected[i][j]==1)
{
U.Union(i,j);
}
}
}
return U.SetCount();
}