摘要

我们为元学习提出了一个算法是模型无关$model-agnostic$.
在某种意义上，其与用梯度下降训练的模型是兼容的，可以应用在大量不同的学习问题上。包括：分类、回归、和加强学习。

• 元学习的目标是正在学习任务上变体的$model$。
• 其能够仅使用小数量的训练示例去解决新的正在学习的任务
• learning task
  在我们的方法中，模型的参数可以明确的被训练，这样，
• a small number of gradient steps with a small amount
  of training data from a new task，在这些任务上将会产生更好的泛化性能。
• 有效地，我们的方法训练一个模型可以容易微调，
• 方法在$twofew-shotimageclassification基准数据集上$可以得到顶级的效果。
• few-shot regression 上产生好的效果》
• 为使用神经网络策略的梯度强化学习，加速微调。

介绍

• 迅速的学习人工智能标志，其涉及从一些示例中识别目标，在只有几秒的实验中迅速的学习新技能。
• 继续将更多的数据变成可利用的。
• 快速灵活的种类是具有挑战性的。代理可以用一小数量的新信息，整合其先前经验。这可以避免在新数据上的过拟合。
• 元学习算法是普遍的和模型无关的。
• 某种意义上其能够被应用在任何学习问题上，使用一个梯度下降程序训练模型，我们聚焦在深度神经网络模型，
• 我们表明，我们的方法如何处理更容易的处理不同的架构和不同的问题序列。problem settings
• 包括：分类、回归和策略梯度加强学习。
  *** classification
• regression
• policy gradient reinforcement learning**
  在元学习中，训练模型的目标是可以迅速学习一个新任务，从新数据的小数量上。通过其$themeta-learner$训练的模型有能力去学习大量的不同任务。
• 我们的方法潜在的关键思想是训练模型的初始化参数$initialparameters$，模型在参数更新之后有最大的效果。
• 与先前的元学习方法不同的是，学习一个更新参数和学习规则。我们的方法即没有扩展学习参数的数量，也没有要求一个$arecurrentmodel$或孪生神经网络$Siamesenetwork$来约束模型架构，其能够用全连接、卷积、循环神经网络真实的结合。
  *** * fully connected,
• convolutional, or
• recurrent neural networks**
• 其也能够使用某种损失函数，
  differentiable supervised losses
  non-differentiable reinforcement learning objectives
  非可微分的加强学习目标

训练模型参数的过程

• a few gradient steps,
• even a single gradient step
• 从特征学习浏览的新任务可以产生好的效果。
• 构建一个内部的表示可以广泛的适用于许多任务。
• 如果内部表示适合于许多任务，简单的微调参数。
• *（在前馈网络中，初始化修改这个顶层权重）
• *有效地，我们的程序优化模型是是容易的和快速微调的 。

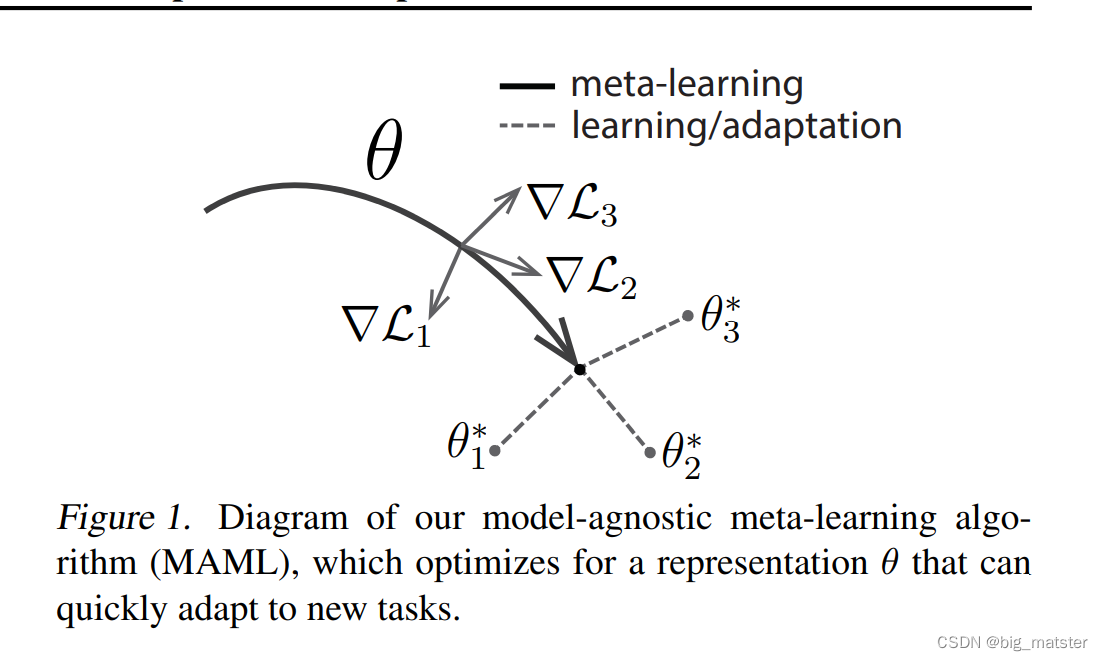
. Model-Agnostic Meta-Learning

• 我们的目的是训练模型能够实现$rapidadaptation$
• 问题序列可以被形式化为一个少样本学习。
• 在这篇文章中，我们将定义问题的步骤和提出我们算法的一般形式。

. Meta-Learning Problem Set-Up

• 少样本元学习的目标是训练一个能迅速适应新任务的模型，使用一个小的数据点和训练迭代。
• 为了完成这些，一系列任务整个元学习阶段训练的模型或$learner$,
• the trained model can quickly adapt to
  new tasks using only a small number of examples or trials.
  少量的例子或实验,训练的模型可以迅速的适应新任务。
  实际上，元学习任务可以将完整的任务作为训练示例，在这篇文章中，我们以一般的方式形式化元学习问题示例，包括，不同的学习领域的简介示例,在章节3，我们将会详细的讨论两个不同的学习域。
• 我们考虑一个模型denote $f$,
• map observation $x$ to outputs $a$ $\to$ $f$
• 整个元学习期间，训练的模型有能力去训练大量而且有限数量的任务。
• 我们想要将我们的框架应用倒多种学习问题上
  • Classification and reinforcement learning 分类到加强学习
  • 形式化 each task
    $$T=L(x_1,a_1,...,x_H,a_H),q(x_1),q(x_{t+1}|x_t,a_t),H$$
• a loss function $L$
• a distribution over initial observations $q(x_1)$
• a transition distribution $q(x_{t+1}|x_t,a_t)$
• an episode length $H$
• supervised learning problems $H=1$
• The model may generate samples
  of length $H$ by choosing an outpu t$a_t$ at each time $t$
• a Markov decision process. 马尔可夫决策过程
• The loss $L(x_1,a_1,...,x_H,a_H)\to R$
• 提供一个特定任务的反馈。
• which might be in the form of a misclassification
  loss or a cost function in a Markov decision process.
• Markov decision process： 马尔可夫决策过程中
  
  

A Model-Agnostic Meta-Learning Algorithm

• nonparametric methods 非参数方法

• recurrent neural works： 双向循环神经网络

• feature embeddings： 在测试阶段，结合非参数方法的特征嵌入。

• a gradient-based learning rule on a new task : 基于梯度学习的规则.

• 

• Species of MAML

• specific instantiations 特定实例化

Supervised Regression and Classification

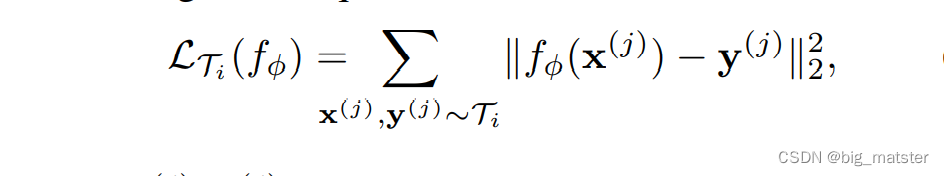
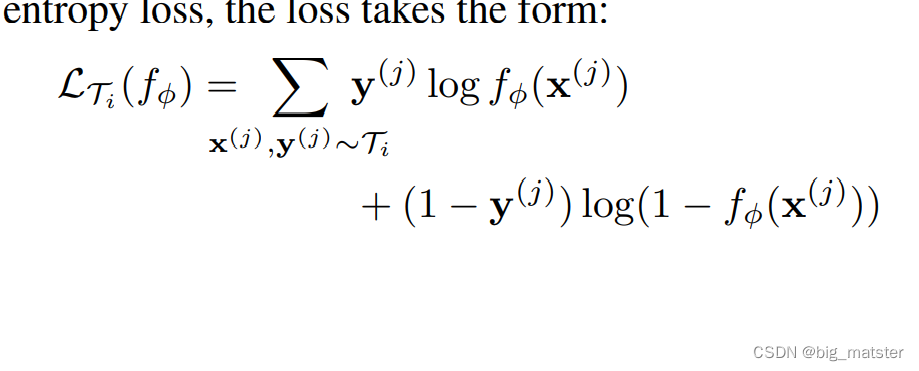
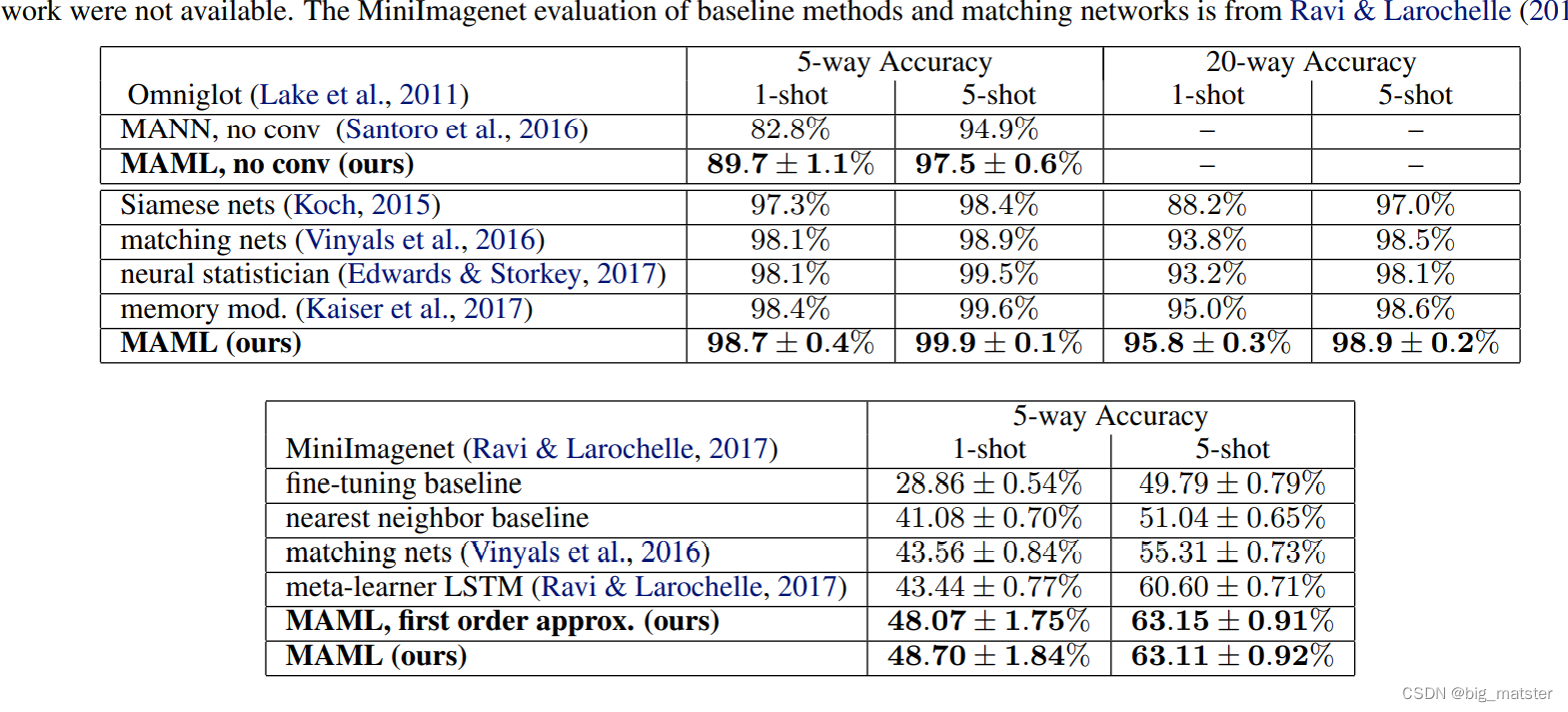
总结

到这吧，抽时间，将元学习框架的啥都学习完整，全部都将其搞定都行啦的理由与打算，慢慢的将其全部都搞定，将元学习啥的全部都搞定。