文章目录
- 1 什么是堆
- 2 堆的实现思路
- 2.1 大根堆的成员变量简介
- 2.2 树的相关知识复习
- 2.3 向下调整创建大根堆
- 2.4 堆的插入
- 2.5 堆的删除
- 3 大根堆实现代码及测试
- 4 PriorityQueue的使用
- 4.1 特性简介
- 4.2 常用方法
- 4.3 使用PriorityQueue实现大根堆
- 写在最后
1 什么是堆
堆实质上就是对完全二叉树进行了一些调整。而在 Java 的 PriorityQueue 优先级队列中,底层就是堆这样的结构。所以,我们尝试通过模拟堆的实现,来更好的理解优先级队列。
知识补充:何为完全二叉树?
答:一棵深度为k的有n个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树。
对于一组关键码集合K = {k0, k1, k2, k3, …, kn-1}来说,如果对于所有的 k ,都满足 ki >= k2i+1 且 ki >= k2i+2,则说明该堆是个大根堆。反之,则称为小根堆。
最直观的感受就是,对于大根堆来说,其根节点是最大的;对于,小根堆来说,其根节点是最小的。
我们以序列:{3, 7, 4, 2, 1, 8, 9, 10, 5} 为例,构造出大根堆如下图所示:
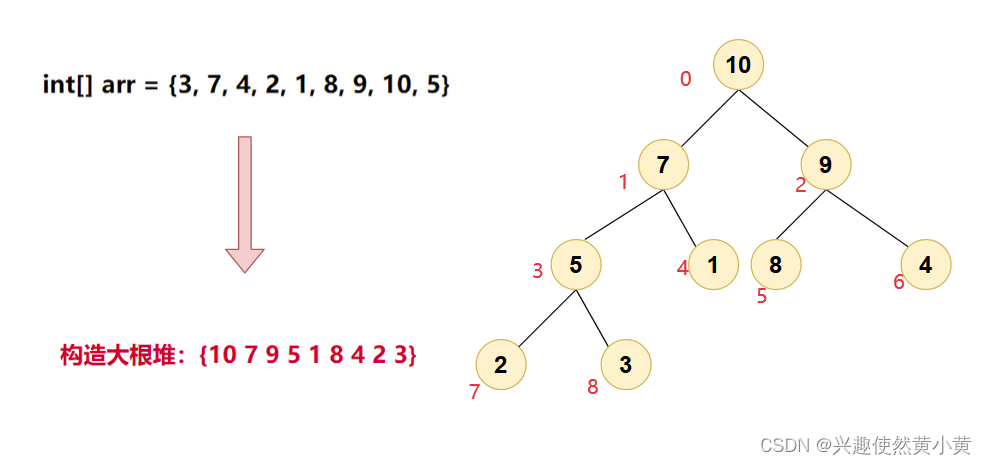
图中,红色序号为元素对应的数组下标,从左到右从上到下,从0开始依次编号。观察堆,可以总结出如下的特点:
- 堆的某个节点的值总是不小于或者不大于父节点的值;
- 堆总是一颗完全二叉树。
本文,将以大根堆为例,简述构造大根堆思路,并使用Java语言进行实现。
2 堆的实现思路
2.1 大根堆的成员变量简介
具体可见图中的代码注释,笔者对于大根堆的实现,都封装在BigHeap类中。

2.2 树的相关知识复习
对于堆来说,其是对完全二叉树进行了些许调整,而如果我们使用顺序存储结构来表示堆,那么,对于双亲节点和孩子节点有如下的性质,在本文中,我们约定,所有的双亲节点采用parent指代,所有的孩子节点,采用child指代。而正如第一部分我们所叙述的一样,编号从上到下,从左到右依次从0开始编号。
- 对于父亲节点 parent,其左孩子和有孩子的编号分别为2 * parent + 1, 2 * parent + 2;
- 对于孩子节点child,其父亲节点满足 parent = (child - 1)/ 2;
- 对于上述两点性质,均需要满足编号在 0 到 useSize-1 之间的边界范围。
2.3 向下调整创建大根堆
那么对于一个序列:{3, 7, 4, 2, 1, 8, 9, 10, 5},我们如何将其转化成为大根堆呢?
思路如下:
-
将该序列从左到右,从上到下,依次编号,构造完全二叉树后如图所示,所有蓝色圆圈中均为parent节点;

-
最后一个 parent 节点的序号满足 (useSize-1-1)/ 2 ,我们从最后一个parent节点开始,依次向前调整,对于每个子树我们采用 向下调整 的策略;
-
从2所对应的紫色框的子树开始,判断parent与左右孩子的值之间的大小关系,将孩子节点中的较大值与parent节点进行比较,如果满足child > parent则进行交换,如图所示,此时,以2为根节点的子树已经调整为了大根堆;

-
继续向前寻找parent节点,调整以4为根节点的子树,转化成大根堆,如图所示;

-
调整以7为根节点的子树,将其向下调整为大根堆,7和10交换后,以7为根节点的新子树也需要调整为大根堆,但是由于其已经满足大根堆了,所以不作交换;

-
最后调整以3为根节点的树,将其调整为大根堆,即将序列转化成了大根堆。

相关代码如下:
// 根据给定的数组向下调整构建大根堆 时间复杂度O(n)
public void creadHeap(int[] data){
// 依次向下调整初始数组的每一个元素 构建成堆
// 从后往前找父节点
this.elements = data;
this.useSize = data.length;
for (int parent = (useSize-1-1) / 2; parent >= 0; parent--) {
siftDown(parent, useSize);
}
}
// 向下调整
// parent为要调整的父节点 len为每颗子树的调整范围
private void siftDown(int parent, int len){
int child = 2 * parent + 1; // 找到左孩子
while (child < len){
if (child + 1 < len && elements[child+1] > elements[child]){
child = child + 1; // 保证child指向的位置一定是子节点中最大的 再与parent进行比较
}
if (elements[child] > elements[parent]){
swap(elements, child, parent);
parent = child; // 继续向下调整
child = 2 * parent + 1;
}else {
break;
}
}
}
2.4 堆的插入
思路如下:
- 先将元素放入堆的末尾,即最后一个孩子之后。从 elements 数组的角度来说,即将新插入的 val 放入到 elements[useSize] 的位置(需要注意是否需要扩容);
- 将新插入的节点依次与双亲节点进行比较,向上调整, 直到与位置为 0 的 parent 比较后,调整完毕,此时,插入新节点后的新堆同样满足大根堆。
我们以插入一个新值val = 99来举例,示意图如下:
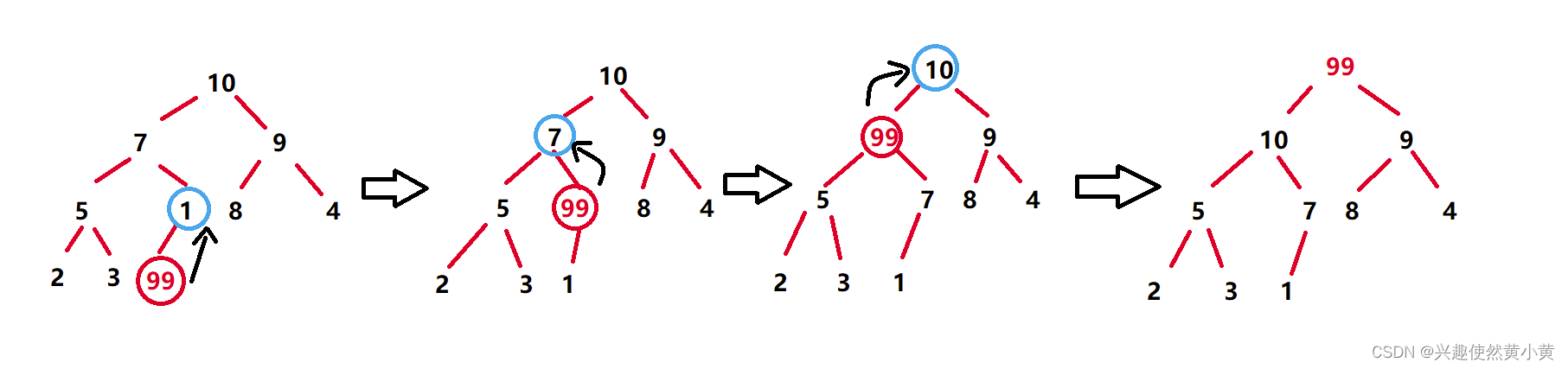
可以发现,每次只需要让新插入的节点和parent进行比较。
为什么不需要和兄弟节点再比较,选出较大值与parent节点进行交换呢?
因为,在每次插入新val前,已经有的元素均满足大根堆的性质,也就是说,对于每一个子树而言,其parent节点都是最大值,所以,就不需要和兄弟节点进行比较了。如果新插入的节点比parent大,其一定比兄弟节点大!
相关代码如下:
// 判断堆是否为满
public boolean isFull(){
return useSize == elements.length;
}
// 入堆
public void offer(int val){
if (isFull()){
elements = Arrays.copyOf(elements, elements.length + DEFAULT_CAPACITY); // 扩容
}
elements[useSize++] = val;
// 向上调整
siftUp(useSize-1);
}
// 向上调整 用于插入元素 每次插入元素放入数组最后的位置(注意容量) 然后向上调整重新构造
private void siftUp(int child){
// 依次与parent比较 若比parent大 则交换
int parent = (child - 1) / 2;
while (parent >= 0){
if (elements[parent] < elements[child]){
swap(elements, parent, child);
child = parent;
parent = (child - 1) / 2;
}else {
break;
}
}
}
2.5 堆的删除
而堆的删除,我们约定,删除的一定是 堆顶元素!
思路如下:
- 将堆顶元素与最后一个元素进行交换;
- 堆的有效数据减少一个,即 useSize = useSize - 1;
- 对堆顶元素进行向下调整,使其结果满足大根堆。
我们以删除 val = 99 为例,示意图如下:
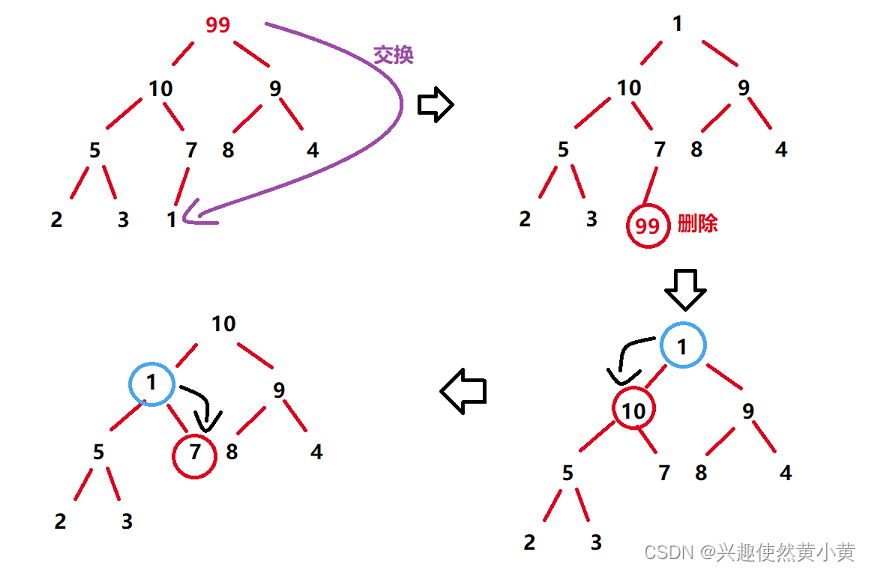
相关代码如下:
// 判断是否为空
public boolean isEmpty(){
return useSize == 0;
}
// 删除堆顶元素 让堆顶元素和最后一个值替换 useSize-- 并且重新向下调整以堆顶元素起始的堆
public int pop(){
if (isEmpty()){
throw new RuntimeException("堆为空");
}
int ret = elements[0];
swap(elements, 0, useSize-1);
useSize--;
// 向下调整
siftDown(0, useSize);
return ret;
}
3 大根堆实现代码及测试
在具体实现代码中,笔者额外实现了TopK问题,具体思路可以看代码注释,附上oj链接:最小k个数,读者可以自行练习。
import java.util.Arrays;
import java.util.Comparator;
import java.util.PriorityQueue;
import java.util.Queue;
/**
* @author 兴趣使然黄小黄
* @version 1.0
* 大根堆
*/
@SuppressWarnings({"all"})
public class BigHeap {
private int[] elements; // 存储堆的元素
private int useSize; // 堆的大小
private final int DEFAULT_CAPACITY = 10; // 默认容量
public BigHeap(){
this.elements = new int[DEFAULT_CAPACITY]; // 默认初始堆的大小为10
this.useSize = 0;
}
// 根据给定的数组向下调整构建大根堆 时间复杂度O(n)
public void creadHeap(int[] data){
// 依次向下调整初始数组的每一个元素 构建成堆
// 从后往前找父节点
this.elements = data;
this.useSize = data.length;
for (int parent = (useSize-1-1) / 2; parent >= 0; parent--) {
siftDown(parent, useSize);
}
}
// 向下调整
// parent为要调整的父节点 len为每颗子树的调整范围
private void siftDown(int parent, int len){
int child = 2 * parent + 1; // 找到左孩子
while (child < len){
if (child + 1 < len && elements[child+1] > elements[child]){
child = child + 1; // 保证child指向的位置一定是子节点中最大的 再与parent进行比较
}
if (elements[child] > elements[parent]){
swap(elements, child, parent);
parent = child; // 继续向下调整
child = 2 * parent + 1;
}else {
break;
}
}
}
// 判断堆是否为满
public boolean isFull(){
return useSize == elements.length;
}
// 入堆
public void offer(int val){
if (isFull()){
elements = Arrays.copyOf(elements, elements.length + DEFAULT_CAPACITY); // 扩容
}
elements[useSize++] = val;
// 向上调整
siftUp(useSize-1);
}
// 向上调整 用于插入元素 每次插入元素放入数组最后的位置(注意容量) 然后向上调整重新构造
private void siftUp(int child){
// 依次与parent比较 若比parent大 则交换
int parent = (child - 1) / 2;
while (parent >= 0){
if (elements[parent] < elements[child]){
swap(elements, parent, child);
child = parent;
parent = (child - 1) / 2;
}else {
break;
}
}
}
// 判断是否为空
public boolean isEmpty(){
return useSize == 0;
}
// 删除堆顶元素 让堆顶元素和最后一个值替换 useSize-- 并且重新向下调整以堆顶元素起始的堆
public int pop(){
if (isEmpty()){
throw new RuntimeException("堆为空");
}
int ret = elements[0];
swap(elements, 0, useSize-1);
useSize--;
// 向下调整
siftDown(0, useSize);
return ret;
}
// 交换arr的i j位置值
private void swap(int[] arr, int i, int j){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
// 求前k个最大的值 则构造有k个元素的最小堆 每次入堆的时候和堆顶进行比较 若更大 则替换 最终剩下的就是前k个最大的值
public int[] maxK(int[] arr, int k) {
int[] ret = new int[k];
// 合法性检验
if(arr == null || k == 0) {
return ret;
}
if(arr.length >= k){
ret = Arrays.copyOf(arr, k);
return ret;
}
Queue<Integer> minHeap = new PriorityQueue<>(k);
//1、遍历数组的前K个 放到堆当中
for(int i = 0; i < k; i++){
minHeap.offer(arr[i]);
}
//2、遍历剩下的K-1个,每次和堆顶元素进行比较
for (int i = k; i < arr.length; i++) {
if (arr[i] > minHeap.peek()) {
minHeap.poll(); // 出堆顶后添加
minHeap.offer(arr[i]);
}
}
//3、存储结果
for (int i = 0; i < k; i++) {
ret[i] = minHeap.poll();
}
return ret;
}
// 求前k个最小的值 构造大顶堆 如果新值比堆顶还要小 则替换 重新构造堆
public int[] smallestK(int[] arr, int k) {
int[] ret = new int[k];
// 合法性检验
if (arr == null || k <= 0){
return ret;
}
if (k >= arr.length){
ret = Arrays.copyOf(arr, k);
}
// 构造大顶堆
Queue<Integer> maxHeap = new PriorityQueue<>(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2 - o1;
}
});
// 先将前k个值入堆
for (int i = 0; i < k; i++) {
maxHeap.offer(arr[i]);
}
// 后判断剩余n-k个元素 如果比堆顶还要小 则替换
for (int i = k; i < arr.length; i++) {
if (arr[i] < maxHeap.peek()){
maxHeap.poll();
maxHeap.offer(arr[i]);
}
}
// 存储并返回结果
for (int i = 0; i < k; i++) {
ret[i] = maxHeap.poll();
}
return ret;
}
// 以数组方式输出堆
public void showHeap(){
for (int i = 0; i < useSize; i++) {
System.out.print(elements[i] + " ");
}
System.out.println();
}
}
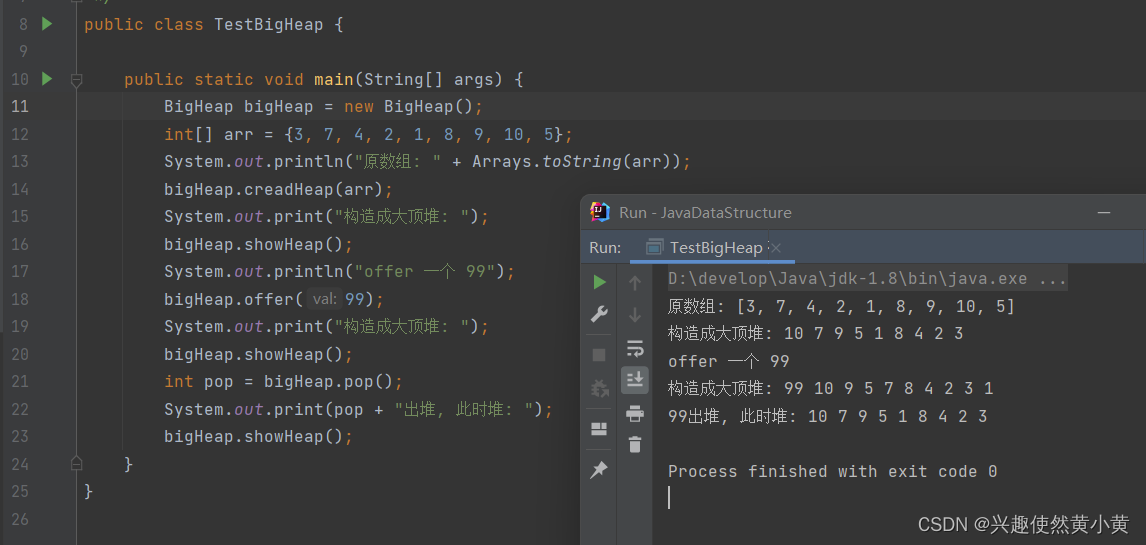
测试代码及测试结果如图:
4 PriorityQueue的使用
4.1 特性简介
Java集合框架中提供了PriorityQueue和PriorityBlockingQueue两种类型的优先级队列,PriorityQueue是线程不安全的,PriorityBlockingQueue是线程安全的。 其继承体系如下:
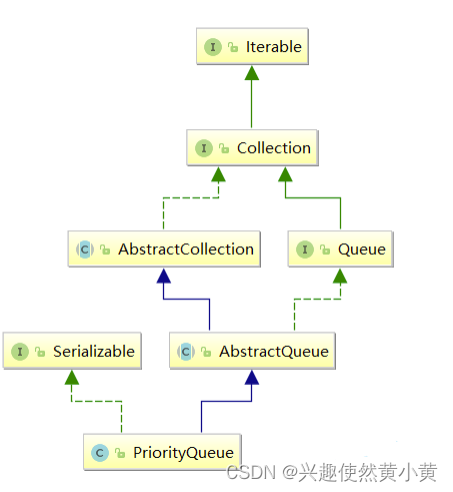
几点说明:
- PriorityQueue中放置的元素 必须要能够比较大小, 不能插入无法比较大小的对象,否则会抛出ClassCastException异常
- 不能插入null对象, 否则会抛出NullPointerException
- 插入和删除元素的时间复杂度为O(logn)
- PriorityQueue底层使用了堆数据结构
- PriorityQueue默认情况下是小堆
4.2 常用方法
常用构造方法如下:

常用方法如下:

其余未列举的方法,读者可以自行参考帮助文档。
4.3 使用PriorityQueue实现大根堆
刚刚提到,默认情况下 PriorityQueue 实现的是小根堆,那么如何实现大根堆呢?
其实,只需要传入比较器,更改比较规则即可。在下面的代码样例中,笔者将一个存Integer对象的优先级队列,以大根堆的形式进行实现:
// 构造大顶堆
Queue<Integer> maxHeap = new PriorityQueue<>(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2 - o1;
}
});
// 构造大顶堆 lambda
Queue<Integer> maxHeap2 = new PriorityQueue<>(((o1, o2) -> {
return o2.compareTo(o1);
}));
写在最后
本文被 Java数据结构 收录点击订阅专栏 , 持续更新中。
创作不易,如果你有任何问题,欢迎私信,感谢您的支持!