个人主页 ： zxctscl
如有转载请先通知

1. 704. 二分查找

1.1 分析

用两个指针，一个在前面left，一个在后面right，求出中间值half，与目标值比较。如果相等，就直接返回下标；如果小于目标值，说明值在后面的区间，此时更新一下left=half+1;如果如果大于目标值，说明值在前面的区间，此时更新一下right=half-1。如果区间都找完没有，就返回-1。

1.2 代码

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left=0,right=nums.size()-1;
  
        while(left<=right)
        {
            int half=left+(right-left)/2;
            if(nums[half]<target)
            {
                left=half+1;
            }
            else if(nums[half]>target)
            {
                right=half-1;
            }
            else  return half;
        }
       return -1;
    }
};

2. 34. 在排序数组中查找元素的第一个和最后一个位置

2.1 分析

寻找左边界：
我们注意到以左边界划分的两个区间的特点：
左边区间 [left, resLeft - 1] 都是小于x 的；右边区间（包括左边界） [resLeft, right] 都是等于等于 x 的；因此，关于 mid 的落点，我们可以分为下面两种情况：◦ 当我们的 mid 落在 [left, resLeft - 1] 区间的时候，也就是 arr[mid] < target 。说明 [left, mid] 都是可以舍去的，此时更新 left 到 mid + 1 的位置，继续在 [mid + 1, right] 上寻找左边界；当 mid 落在 [resLeft， right] 的区间的时候，也就是 arr[mid] >= target 。
说明 [mid + 1, right] （因为 mid 可能是最终结果，不能舍去）是可以舍去的，此时更新 right 到 mid 的位置，继续在 [left, mid] 上寻找左边界；
注意：这里找中间元素需要向下取整。
因为后续移动左右指针的时候：
• 左指针： left = mid + 1 ，是会向后移动的，因此区间是会缩⼩的；
• 右指针： right = mid ，可能会原地踏步（比如：如果向上取整的话，如果剩下 1,2 两个元素， left == 1 ， right == 2 ， mid == 2 。更新区间之后， left，right，mid 的值没有改变，就会陷入死循环）。因此⼀定要注意，当 right = mid 的时候，要向下取整。

寻找右边界思路：
寻右左边界：
⽤ Right 表示右边界；
我们注意到右边界的特点：
左边区间 （包括右边界） [left, Right] 都是小于等于 x 的；右边区间 [resRight+ 1, right] 都是大于 x 的；因此，关于 mid 的落点，我们可以分为下面两种情况：当我们的 mid 落在 [left, Right] 区间的时候，说明 [left, mid - 1]（ mid 不可以舍去，因为有可能是最终结果） 都是可以舍去的，此时更新 left 到 mid的位置； 当 mid 落在 [Right+ 1, right] 的区间的时候，说明 [mid, right] 内的元素是可以舍去的，此时更新 right 到 mid - 1 的位置；
注意：这⾥找中间元素需要向上取整。
因为后续移动左右指针的时候：
• 左指针： left = mid ，可能会原地踏步（比如：如果向下取整的话，如果剩下 1,2 两个元素， left == 1， right == 2，mid == 1 。更新区间之后， left，right，mid 的值没有改变，就会陷⼊死循环）。
• 右指针： right = mid - 1 ，是会向前移动的，因此区间是会缩小的；
因此⼀定要注意，当 right = mid 的时候，要向下取整。

2.2 代码

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target)
    {
        if (nums.size() == 0) return { -1, -1 };

        int begin = 0;
        // 1. ⼆分左端点
        int left = 0, right = nums.size() - 1;
        while (left < right)
        {
            int mid = left + (right - left) / 2;
            if (nums[mid] < target) left = mid + 1;
            else right = mid;
        }
        // 判断是否有结果
        if (nums[left] != target) return { -1, -1 };
        else begin = left; // 标记⼀下左端点
        // 2. ⼆分右端点
        left = 0, right = nums.size() - 1;
        while (left < right)
        {
            int mid = left + (right - left + 1) / 2;
            if (nums[mid] <= target) left = mid;
            else right = mid - 1;
        }
        return { begin, right };
    }

};

3. 35. 搜索插入位置

3.1 分析

利用二分算法的特性，将区间分为两部分，一部分是小于目标值的，那么这个区间就不考虑了；另一部分是等于等于目标值的，如果等于目标值那么就直接返回这个下标，如果大于目标值，那么这个值也是第一个比目标值大的数，这个位置的数之前就得插入目标值，返回的也是这个下标。

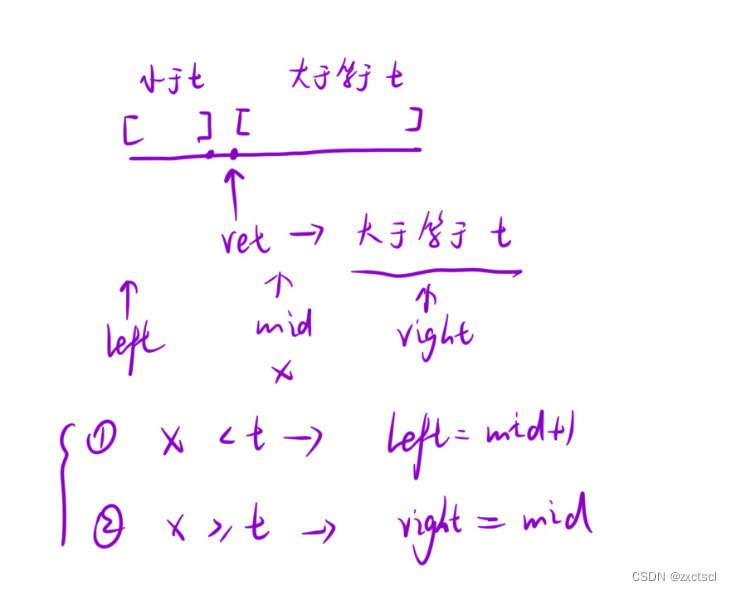
3.2 代码

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
    int left=0,right=nums.size()-1;
    while(left<right)
    {
        int mid=left+(right-left)/2;
        if(nums[mid]<target)left=mid+1;
        else right=mid;
    }
    if (nums[left] < target) return right + 1;
    return left;
    }
};

4. 852. 山脉数组的峰顶索引

4.1 分析

题目给的元素特性很明显，在某一个位置之前的元素都是呈现上升趋势，在它之后都会呈现下降趋势。按照这个特性可以将数组分为两部分：1.mid的值小于mid-1，那么最大值就在前面的区间，那么就更新一下right=mid-1；2.mid的值大于等于mid-1，那么最大值就在后面的区间，更新一下left=mid。最终就找到当循环条件返回left就可以。

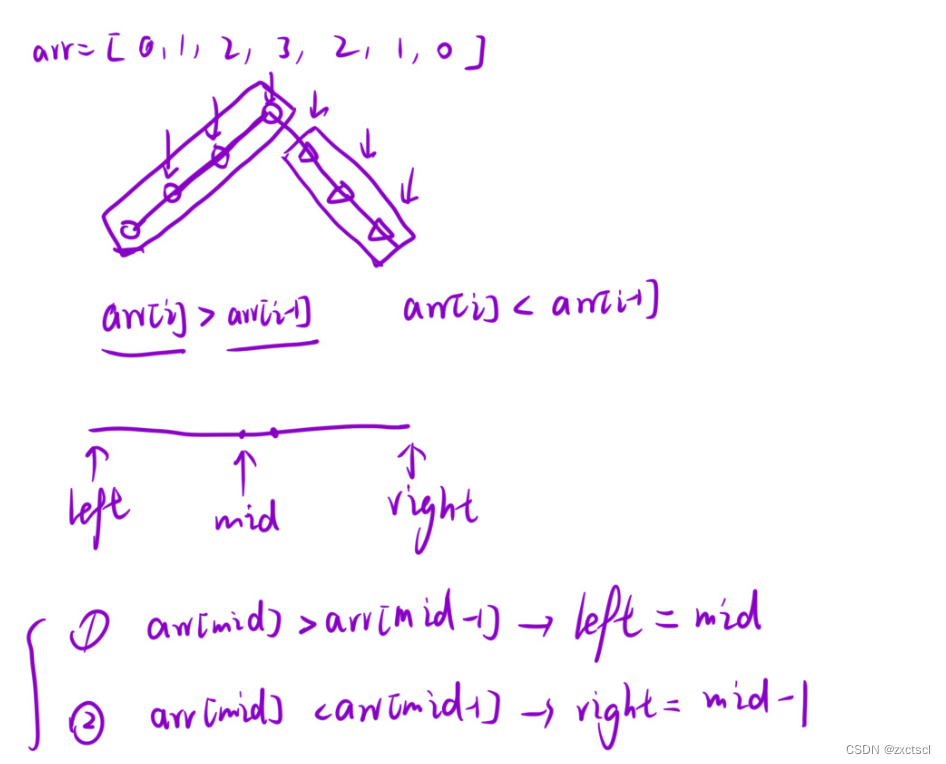
4.2 代码

class Solution {
public:
    int peakIndexInMountainArray(vector<int>& arr) {
    int left=1,right=arr.size()-2;
    while(left<right)
    {
        int mid=left+(right-left+1)/2;
        if(arr[mid]>arr[mid-1])left=mid;
        else right=mid-1;
       
    }
    return left;
    }
};

5. 153. 寻找旋转排序数组中的最小值

5.1 分析

根据题目所给的特性，可以将数组分为两段区间，都是明显呈现递增。第二段区间所有的值都小于第一段。选择最后最后一个值为参考值。如果在mid大于最后一个值，说明最小值在后面的区间，更新一下left=mid+1;如果如果在mid小于等于最后一个值，那么就更新一下right=mid。

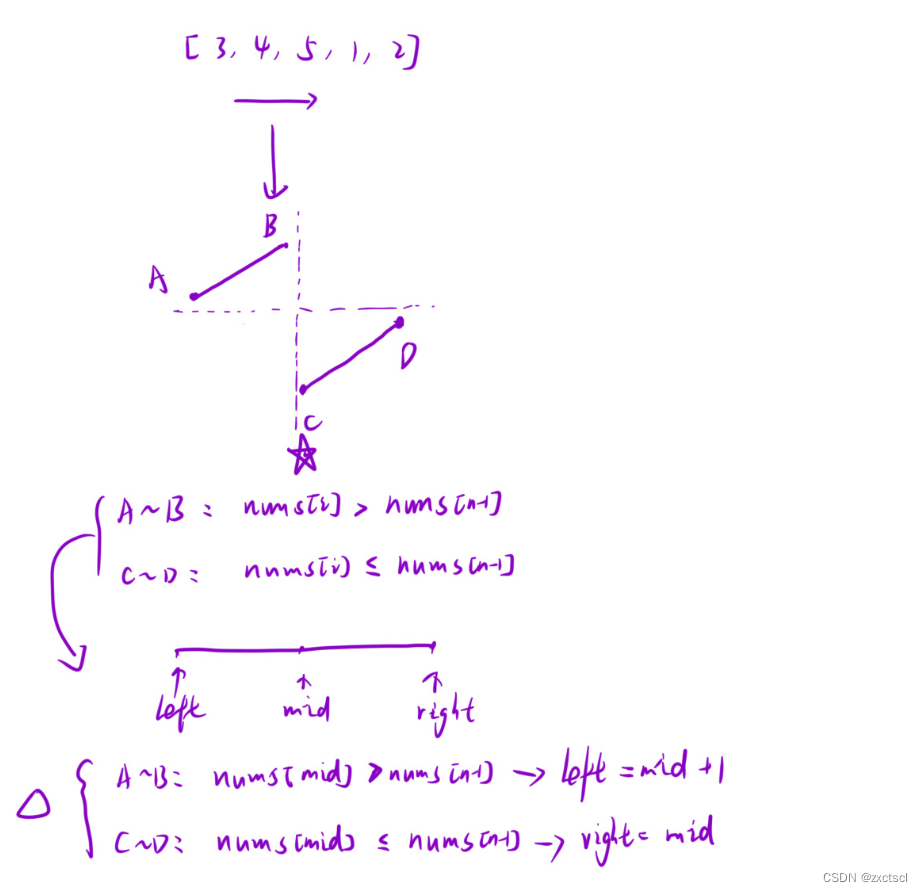
5.2 代码

class Solution {
public:
    int findMin(vector<int>& nums) {
     int left=0,right=nums.size()-1;
     int x=nums[right];
    while(left<right)
    {
        int mid=left+(right-left)/2;
        if(nums[mid]>x)left=mid+1;
        else right=mid;
       
    }
    return nums[left];
    }
};

6. 二分算法模板

定义两个指针，然后找符合条件的情况按下面的模板走。
填上对应的if表达式，返回题目要求的值即可。

有问题请指出，大家一起进步！！！