机器学习中的最优化算法有哪些？

我们日常生活中遇到过很多最优化问题，比如如何在最短时间内从A点到达B点？如何投入最少工作量却获得最大的效益？如何设计发动机使得油耗最少而功率最大？可见，最优化的作用十分强大。接下来，我们介绍几个最优化算法，并利用它们训练出一个非线性函数用于分类。

1、Logistic回归

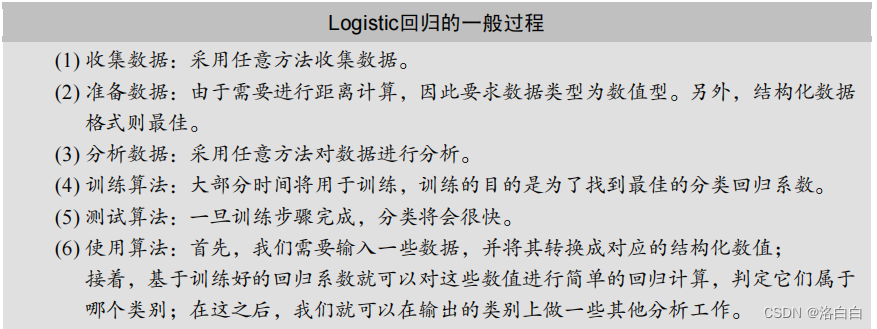在这里插入图片描述 **优点：**计算代价不高，易于理解和实现。
缺点：容易欠拟合，分类精度可能不高。
适用数据类型：数值型和标称型数据。

我们想要的函数应该是，能接受所有的输入然后预测出类别。例如，在两个类的情况下，上述函数输出0或1。或许你之前接触过具有这种性质的函数，该函数称为海维塞德阶跃函数（Heaviside step function），或者直接称为单位阶跃函数。然而，海维塞德阶跃函数的问题在于：该函数在跳跃点上从0瞬间跳跃到1，这个瞬间跳跃过程有时很难处理。幸好，另一个函数也有类似的性质①，且数学上更易处理，这就是Sigmoid函数。Sigmoid函数具体的计算公式如下：
在这里插入图片描述

图1给出了Sigmoid函数在不同坐标尺度下的两条曲线图。
当x为0时，Sigmoid函数值为0.5。
随着x的增大，对应的Sigmoid值将逼近于1；
而随着x的减小，Sigmoid值将逼近于0。
如果横坐标刻度足够大（图1下图），Sigmoid函数看起来很像一个阶跃函数。
在这里插入图片描述因此，为了实现Logistic回归分类器，我们可以在每个特征上都乘以一个回归系数，然后把所有的结果值相加，将这个总和代入Sigmoid函数中，进而得到一个范围在0~1之间的数值。任何大于0.5的数据被分入1类，小于0.5即被归入0类。所以，Logistic回归也可以被看成是一种概率估计。

确定了分类器的函数形式之后，现在的问题变成了：最佳回归系数③是多少？如何确定它们的大小？

2、基于最优化方法的最佳回归系数确定

Sigmoid函数的输入记为z，由下面公式得出：
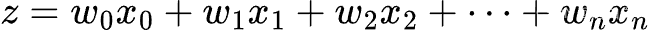在这里插入图片描述如果采用向量的写法，上述公式可以写成z = wT x，它表示将这两个数值向量对应元素相乘然后全部加起来即得到z值。其中的向量x是分类器的输入数据，向量w也就是我们要找到的最佳参数（系数），从而使得分类器尽可能地精确。为了寻找该最佳参数，需要用到最优化理论的一些知识。

2.1 梯度上升法

梯度上升法基于的思想是：要找到某函数的最大值，最好的方法是沿着该函数的梯度方向探寻。如果梯度记为∇，则函数f(x,y)的梯度由下式表示：
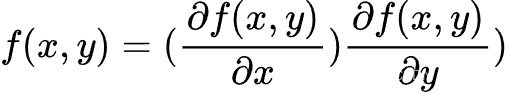
在这里插入图片描述
这是机器学习中最易造成混淆的一个地方，但在数学上并不难，需要做的只是牢记这些符号的意义。这个梯度意味着要沿x的方向移动 $\frac { \partial f ( x , y ) } { \partial x }$ ，沿y的方向移动 $\frac { \partial f ( x , y ) } { \partial y }$ 其中，函数f (x,y) 必须要在待计算的点上有定义并且可微。一个具体的函数例子见图2。

梯度上升算法到达每个点后都会重新估计移动的方向。从P0开始，计算完该点的梯度，函数就根据梯度移动到下一点P1。在P1点，梯度再次被重新计算，并沿新的梯度方向移动到P2。如此循环迭代，直到满足停止条件。迭代的过程中，梯度算子总是保证我们能选取到最佳的移动方向图2中的梯度上升算法沿梯度方向移动了一步。可以看到，梯度算子总是指向函数值增长最快的方向。这里所说的是移动方向，而未提到移动量的大小。该量值称为步长，记做α。用向量来表示的话，梯度上升算法的迭代公式如下：
$\alpha \nabla _ { w } f ( w )$
该公式将一直被迭代执行，直至达到某个停止条件为止，比如迭代次数达到某个指定值或算法达到某个可以允许的误差范围。

2.2 梯度下降算法

在这里插入图片描述基上面的内容，我们来看一个Logistic回归分类器的应用例子，从图3可以看到我们采用的数据集。

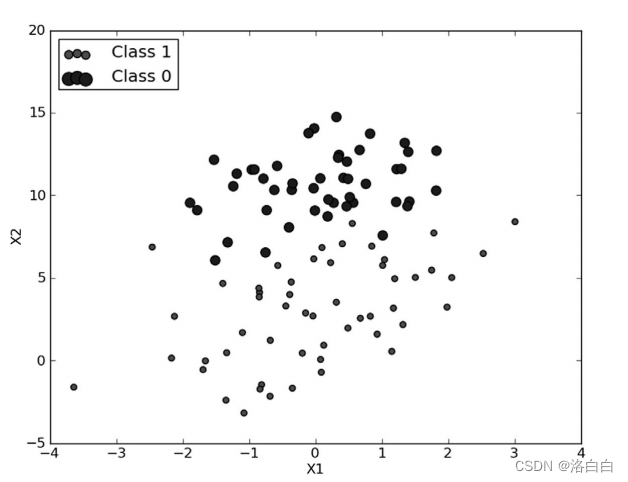
一个简单数据集，下面将采用梯度上升法找到Logistic回归分类器在此数据集上的最佳回归系数

2.3 训练算法：使用梯度上升找到最佳参数

图3中有100个样本点，每个点包含两个数值型特征：X1和X2。在此数据集上，我们将通过使用梯度上升法找到最佳回归系数，也就是拟合出Logistic回归模型的最佳参数。梯度上升法的伪代码如下：

在这里插入图片描述
下面的代码是梯度上升算法的具体实现。为了解实际效果，打开文本编辑器并创建一个名为 logRegres.py的文件，输入下列代码：

程序清单1 Logistic 回归梯度上升优化算法

def loadDataSet():
    dataMat = []; labelMat = []
    fr = open('testSet.txt')
    for line in fr.readlines():
        lineArr = line.strip().split()
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])  # X0的值初始化设置为1.0
        labelMat.append(int(lineArr[2]))
    return dataMat,labelMat

def sigmoid(inX):
    return 1.0/(1+exp(-inX))
def gradAscent(dataMatIn, classLabels):
    dataMatrix = mat(dataMatIn)             # 转化为 NumPy 矩阵
    labelMat = mat(classLabels).transpose() # 转化为 NumPy 矩阵
    m,n = shape(dataMatrix)  # m=100，n=3，代表100个样本，3个特征（包括X0）
    alpha = 0.001  # 步长，学习速率
    maxCycles = 500 # 最大迭代次数
    weights = ones((n,1))
    for k in range(maxCycles):          # 最大迭代次数
        h = sigmoid(dataMatrix*weights) # 如果两参数都是矩阵，那么*和dot()都为矩阵相乘，而如果两个都是数组，则*为对应位置相乘，dot()为矩阵相乘
        error = (labelMat - h)          # 误差
        weights = weights + alpha * dataMatrix.transpose() * error # 更新权值
    return weights

程序清单1的代码在开头提供了一个便利函数loadDataSet()，它的主要功能是打开文本文件testSet.txt并逐行读取。每行前两个值分别是X1和X2，第三个值是数据对应的类别标签。此外，为了方便计算，该函数还将X0的值设为1.0。接下来的函数是2节提到的函数sigmoid()。

梯度上升算法的实际工作是在函数gradAscent()里完成的，该函数有两个参数。第一个参数是dataMatIn，它是一个2维NumPy数组，每列分别代表每个不同的特征，每行则代表每个训练样本。我们现在采用的是100个样本的简单数据集，它包含了两个特征X1和X2，再加上第0维特征X0，所以dataMathln里存放的将是100×3的矩阵。我们获得输入数据并将它们转换成NumPy矩阵。这是本书首次使用NumPy矩阵，如果你对矩阵数学不太熟悉，那么一些运算可能就会不易理解。比如，NumPy对2维数组和矩阵都提供一些操作支持，如果混淆了数据类型和对应的操作，执行结果将与预期截然不同。

2.4 分析数据：画出决策边界

上面已经解出了一组回归系数，它确定了不同类别数据之间的分隔线。那么怎样画出该分隔线，从而使得优化的过程便于理解呢？

程序清单2：画出数据集和Logistic回归最佳拟合直线的函数

def plotBestFit(weights):
    import matplotlib.pyplot as plt
    print(weights)
    dataMat, labelMat = loadDataSet()
    dataArr = array(dataMat)
    n = shape(dataArr)[0] 
    xcord1 = []; ycord1 = []
    xcord2 = []; ycord2 = []
    for i in range(n):
        if int(labelMat[i])== 1:
            xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
        else:
            xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1, ycord1, s=30, c='red', marker='s') # 画散点图
    ax.scatter(xcord2, ycord2, s=30, c='green')
    x = arange(-3.0, 3.0, 0.1) # 步长0.1
    y = (-weights[0]-weights[1]*x)/weights[2]  # 0=w0x0+w1x1+w2x2，其中x0=1，y即x2
    ax.plot(x, y)
    plt.xlabel('X1'); plt.ylabel('X2');
    plt.show()

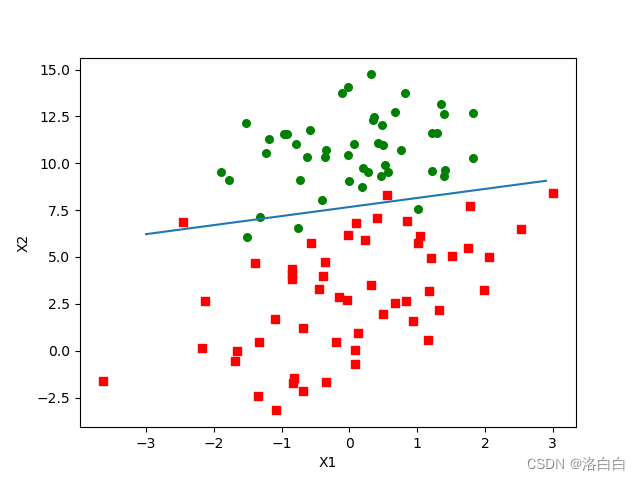
程序清单2中的代码是直接用Matplotlib画出来的。唯一要指出的是，处设置了sigmoid 函数为0。回忆2节，0是两个分类（类别1和类别0）的分界处。因此，我们设定 0 = w0x0 + w1x1 + w2x2，然后解出X2和X1的关系式（即分隔线的方程，注意X0＝1）。

输出的结果如图5-4所示：
在这里插入图片描述
梯度上升算法在500次迭代后得到的Logistic回归最佳拟合直线。

这个分类结果相当不错，从图上看只错分了两到四个点。但是，尽管例子简单且数据集很小，这个方法却需要大量的计算（300次乘法）。因此下一节将对该算法稍作改进，从而使它可以用在真实数据集上。

2.5 训练算法：随机梯度上升

梯度上升算法在每次更新回归系数时都需要遍历整个数据集，该方法在处理100个左右的数据集时尚可，但如果有数十亿样本和成千上万的特征，那么该方法的计算复杂度就太高了。一种改进方法是一次仅用一个样本点来更新回归系数，该方法称为随机梯度上升算法。由于可以在新样本到来时对分类器进行增量式更新，因而随机梯度上升算法是一个在线学习算法。与“在线学习”相对应，一次处理所有数据被称作是批处理。随机梯度上升算法可以写成如下的伪代码：
在这里插入图片描述程序清单3 随机梯度上升算法

def stocGradAscent0(dataMatrix, classLabels):
    m,n = shape(dataMatrix)
    alpha = 0.01
    weights = ones(n)   # 初始化权值为1，这里是列表，不是矩阵
    for i in range(m):  # 对于每个样本
        h = sigmoid(sum(dataMatrix[i]*weights))  # 数值，不是向量
        error = classLabels[i] - h   # 数值，不是向量
        weights = weights + alpha * error * dataMatrix[i]  # 对于每个样本进行权值的更新
    return weights

可以看到，随机梯度上升算法与梯度上升算法在代码上很相似，但也有一些区别：第一，后者的变量h和误差error都是向量，而前者则全是数值；第二，前者没有矩阵的转换过程，所有变量的数据类型都是NumPy数组。

在这里插入图片描述
直接比较程序清单3和程序清单1的代码结果是不公平的，后者的结果是在整个数据集上迭代了500次才得到的。一个判断优化算法优劣的可靠方法是看它是否收敛，也就是说参数是否达到了稳定值，是否还会不断地变化？对此，我们在程序清单53中随机梯度上升算法上做了些修改，使其在整个数据集上运行200次。最终绘制的三个回归系数的变化情况如图6所示。

总结

Logistic回归的目的是寻找一个非线性函数Sigmoid的最佳拟合参数，求解过程可以由最优化算法来完成。在最优化算法中，最常用的就是梯度上升算法，而梯度上升算法又可以简化为随机梯度上升算法。
随机梯度上升算法与梯度上升算法的效果相当，但占用更少的计算资源。此外，随机梯度上
升是一个在线算法，它可以在新数据到来时就完成参数更新，而不需要重新读取整个数据集来进行批处理运算。
机器学习的一个重要问题就是如何处理缺失数据。这个问题没有标准答案，取决于实际应用中的需求。现有一些解决方案，每种方案都各有优缺点。