一.范数(Norms)
1.什么是范数?
范数是一个向量空间V的函数,每一个属于向量空间V的向量x都匹配了一个实数(它的长度):
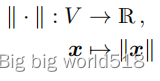
2.范数的性质?
齐次性:
正定性:
三角不等式:
3.什么是曼哈顿范数?
对于(n维向量),
称为曼哈顿范数,也称作
范数
4.什么是欧几里得距离?
对于(n维向量),
称为欧几里得距离,也称作
范数。
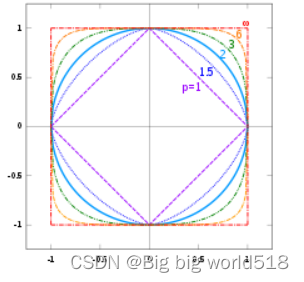
5.向量的p范数?
,当p越大,图像越方,二维情况如下:
二.向量的内积
1.什么是双线性映射(bilinear mapping)?
对于,存在:
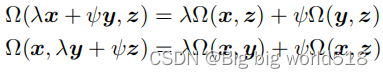
2.什么是内积(Inner product)?
如果V是一个向量空间,并且存在双线性映射,那么
称这个映射是对称的:
称这个映射是正定的:对于任何
一个正定,对称的双线性映射称为向量空间V上的内积(Inner Product),一般写作。
3.什么是内积空间?什么是欧几里得向量空间?
称为内积空间,如果内积操作变为点积,那么称作欧几里得向量空间,这里强调:内积不等于点积,举例:
![]()
4.什么是正定(positive definite)矩阵?什么是半正定矩阵?
存在矩阵A:,那么说明矩阵A是正定的,
如果,那么说明矩阵A是半正定的。
5.正定矩阵有什么性质?
- 正定矩阵A的行列式值
恒为正
- 实对称矩阵A正定当且仅当A与单位矩阵合同
- 若A是正定矩阵,那么A的逆矩阵也是正定矩阵
- 两个正定矩阵的和仍是正定矩阵
- 正实数与正定矩阵的积仍是正定矩阵
三.长度和距离(Length and Distance)
1.什么是柯西不等式?
对于内积空间,存在运算
,使得不等式
成立
2.什么是两个向量之间的距离?什么是两个向量之间的欧几里得距离?
首先介绍距离映射:,对于单个元素:
Distance:对于内积空间来说:
![]()
欧几里得距离:当内积变换为点积的时候,称作欧几里得距离。
其中映射d满足:对称,正定,三角不等式。
四.正交投影(Orthogonal Projection)
1.如何求得二维平面的坐标?投影?投影矩阵?
考虑情况:R2向量空间的向量x向子空间投影到直线b上,投影结果为。
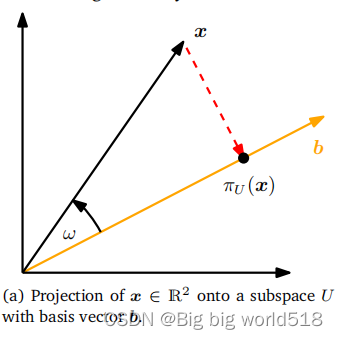
- 求坐标λ,有
,
- 求投影
,求投影长度
- 求投影矩阵
,所以
2.如何求得多维空间的坐标?投影?投影矩阵?
考虑情况:,
x向更低维度的子空间U投影,
。
是U的有序基,投影可以被这些有序基线性表示:
- 求投影的坐标λi,最终得到齐次线性方程组:
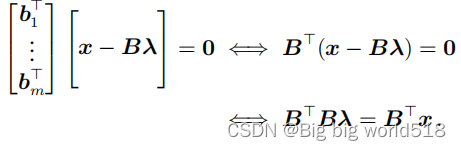
所以有,
- 求投影:
- 求投影矩阵:
,如果基底是正定的,那么
,上面计算可以省略。
3.格拉姆施密特法是什么?
格拉姆施密特就是在相同向量空间V中,给定一组基底,求正交基底。
假定有不平行向量a,b,c,我们需要(1)正交化(如下)(2)单位化(自行考虑)

五.旋转(Rotation)
1.R2空间中矩阵的旋转
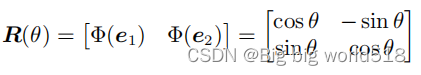
2.R3空间中矩阵的旋转
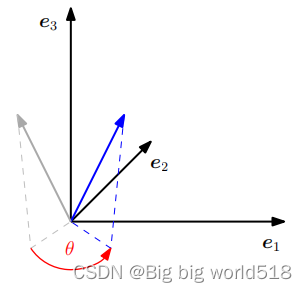
分别关于e1,e2,e3的旋转矩阵:
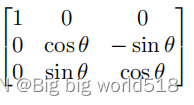
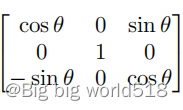
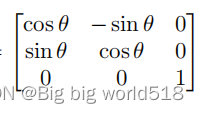
3.吉文斯旋转
六.矩阵的等价、相似、合同
1.什么是矩阵的等价?
矩阵A和B等价的充要条件是对于同型矩阵A和B的秩相等。定义是存在可逆矩阵P和Q,使得A=PBQ。
2.什么是矩阵的合同?
矩阵的合同是指对于同型方阵A和B,存在可逆矩阵P使得。
3.什么是矩阵的相似?
矩阵的相似是指对于同型方阵A和B,存在可逆矩阵P使得。
4.三者关系?
- 等价(只有秩相同)–>合同(秩和正负惯性指数相同)–>相似(秩,正负惯性指数,特征值均相同),矩阵亲密关系的一步步深化。
- 相似矩阵必为等价矩阵,但等价矩阵未必为相似矩阵
- PQ=E的等价矩阵是相似矩阵
- 合同矩阵必为等价矩阵,等价矩阵未必为合同矩阵
- 正惯性指数相同的等价矩阵是合同矩阵
- 合同矩阵未必是相似矩阵
- 相似矩阵未必合同
- 正交相似矩阵必为合同矩阵,正交合同矩阵必为相似矩阵
- 如果A与B都是n阶实对称矩阵,且有相同的特征根.则A与B既相似又合同