一、数据类型

1. unsigned：无符号数类型

当一个数是无符号类型时，那么其最高位的1或0，和其它位一样，用来表示该数的大小。

2.signed：有符号数类型

当一个数是有符号类型时，最高数称为“符号位”。符号位为1时，表示该数为负数，为0时表示为正数。

注意：有符号类型可以表示正数，负数或0，无符号类型仅能表示大于等于0的值

1.1 整型

有符号字符型：(signed) char// 1字节
无符号字符型：unsigned char// 1字节
有符号短整型：(signed) short// 2字节
无符号短整型：unsigned short// 2字节
有符号整型：(signed) int// 4字节
无符号整型：unsigned int// 4字节
有符号长整型：(signed) long// 4字节
无符号长整型：unsigned long// 4字节
有符号更长整型：(signed) long long// 8字节
无符号更长整型：unsigned long long// 8字节

1.2 浮点型

单精度浮点型：float //4字节
双精度浮点型：double //8字节 

1.3 构造类型

数组类型
结构体类型：struct
枚举类型：enum
联合类型：union

1.4 指针类型

//32位环境下指针变量大小 4
//64位环境下指针变量大小 8
字符指针：char*
短整型指针：short*
整型指针：int*
长整型指针：long*
更长类型指针：long long*
单精度浮点数指针：float*
双精度浮点数指针：double*
空类型指针：void*

1.5 空类型

void
//void代表无类型，常用在程序编写中对定义函数的参数类型、返回值、函数中指针类型进行声明。

二、整型的存储

2.1 原码，补码，反码

我们知道计算机存储数据是以二进制的方式，那具体是以怎样的方式存储呢

对于一个数，计算机要使用一定的编码方式进行存储，原码、反码、补码是机器存储一个具体数字的编码方式。

三种方式均有符号位和数值位两部分，符号位都是0表示“正数”，1表示“负数”，而数值位分正负数而定。

正数的原码、反码、补码都相同，负数的原码、反码、补码各不相同

2.1.1 原码

直接将数值按照正负数的形式翻译成二进制就可以得到原码

+5的原码：00000000 00000000 00000000 00000101
-5的原码：10000000 00000000 00000000 00000101

2.1.2 补码

将原码的符号位不变，其他位次按位取反
即：0变为1，1变为0

+5的反码：00000000 00000000 00000000 00000101
-5 的反码：11111111 11111111 11111111 11111010

2.1.3 反码

反码符号位不变，数值为+1

+5的补码：00000000 00000000 00000000 00000110
-5的补码：11111111 11111111 11111111 11111011

反码回到原码的两种方式：

1、补码-1后 取反得到原码
2、补码取反后 +1得到原码

计算机内存数值的存储方式是补码！

2.2 大小端

2.2.1 什么是大小端

大端存储模式：指数据的低位保存在内存的高地址中，而数据的高位保存在内存的低地址中
 
小端存储模式：指数据的低位保存在内存的低地址中，而数据的高位保存在内存的高地址中

具体是什么意思呢~

首先我们得知道内存中数据是以16进制表示的

int a=0x11223344//十六进制

小端存储

44

33

22

11

                                                                低地址                                           高地址

大端存储

11

22

33

44

                                                                低地址                                           高地址

2.2.2 怎么判断大小端

我们可以通过取出第一位，也就是低地址的数来进行判断。

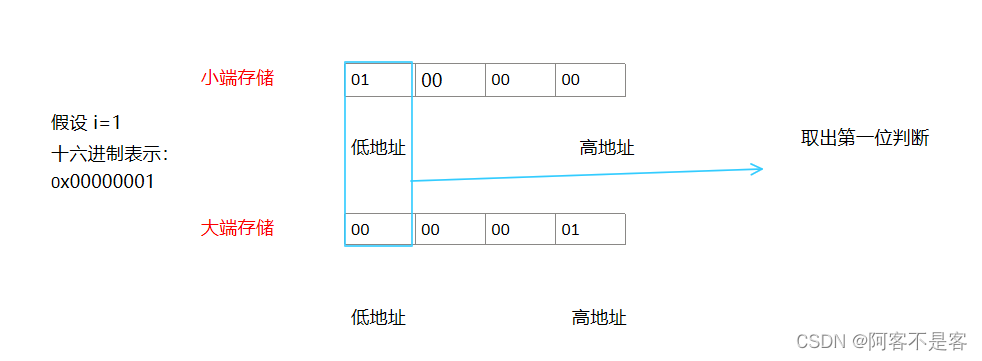
那我们如何取出第一位呢~，这就需要我们对指针的灵活运用了

我们知道第一位相当于一个字节，而char类型就是一个字节，所以用（char*）进行强制类型转换并取出就行了

#include<stdio.h>
int main()
{
	int a = 1;
	char* p = (char*) & a;//强制类型转换
	if (*p == 1)
		printf("小端");
	else
		printf("大端");
	return 0;
}

三、整型截断

整型截断是将所占字节大的元素赋给所占字节小的元素时会出现数值的舍去现象。

简单来说就是将长字节内容截取一部分赋给短字节内容

 char i = -1;//-1是整型4个字节，char类型1个字节，发生整型截断

1. 原码：1000000 0000000 0000000 0000001
2. 反码：11111111 11111111 11111111 11111110
3. 补码：11111111 11111111 11111111 11111111

     char类型有八个比特位，截取后八位

1. i的补码：11111111
2. i的反码：11111110
3. i的原码：1000001

 所以i仍是-1

四、整型提升

C的整型算术运算总是至少以缺省（默认）整型类型的精度来进行的。为了获得这个精度，表达式中的字符和短整型操作数在使用之前被转换为普通整型，这种转换称为整型提升。

有符号的整型提升高位补符号位，无符号的整型提升高位补0。

4.1 正整数的整型提升

 char a=1；
 //补码：00000001
 //有符号，符号位是0，提升为00000000000000000000000000000001

4.2 负数的整型提升

  char b=-1;
  //补码：1111111
  //有符号，符号位是1，提升为11111111111111111111111111111111

4.3 无符号数的整型提升

  unsigned c=-1
   //补码：1111111
   //无符号，补0，提升为00000000000000000000000011111111

五、浮点型在内存中的存储

5.1 浮点型运算规则

要表示浮点数的第一步，就是让小数也能使用二进制来表示。我们知道二进制表示整数时，最低位代表2的0次方，往高位依次是2的1次方，2次方，3次方……那么对应的，二进制数小数点后面，最高位则是2的-1次方，-2次方，-3次方……

根据国际标准IEEE（电⽓和电⼦⼯程协会）754，任意⼀个⼆进制浮点数V可以表⽰成下⾯的形式：

(-1) ^ S * M * 2 ^ E
 
1.  (-1) ^ S 表示符号位，当S=0时，V为正数；当S=1时，V为负数
2.  M 表示有效数字，且1 <= M <2
3.  2 ^ E表示指数位

⼗进制的5.0，写成⼆进制是 101.0 ，相当于 1.01×2^2 。

那么，按照上⾯V的格式，可以得出S=0，M=1.01，E=2。

对于32位的浮点数float，最⾼的1位存储符号位S，接着的8位存储指数E，剩下的23位存储有效数字M

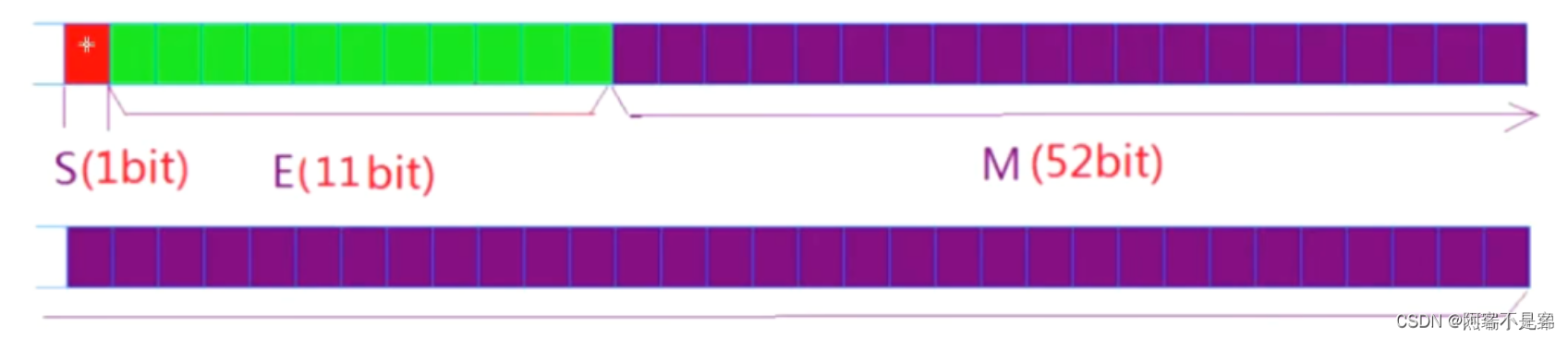
对于64位的浮点数double，最⾼的1位存储符号位S，接着的11位存储指数E，剩下的52位存储有效数字M

5.2 浮点数取得过程

5.2.1 对于M的规定

1 ≤ M < 2 ，即M可以写成1.xxxxxx的形式。IEEE 754规定，在计算机内部保存M时，默认这个数的第一位总是1，因此可以被舍去，只保存后面的xxxxxx部分。比如保存1.01的时候，只保存01，等到读取的时候，再把第一位的1加上去。这样做的目的，是节省1位有效数字。以32位浮点数为例，留给M只有23位，将第一位的1舍去以后，等于可以保存24位有效数字。

5.2.2 对于E的规定

1. E不全为0或不全为1

这时，浮点数就采⽤下⾯的规则表⽰，即指数E的计算值减去127（或1023），得到真实值，再将有效数字M前加上第⼀位的1。

如一个浮点数存储方式如下：

0 01111110 00000000000000000000000

1. 首先将 01111110 转换为十进制为126
2. 再将126-127=-1，所以指数位为-1
3. 有效数字部分为0，所以表示1.0
4. 符号位0，是个正数，所以表示的浮点数是1.0*2^-1=0.5

2. E全为0

这时候指数为0-127，最后肯定得到一个很小的数，所以特别规定

这时，浮点数的指数E等于1-127（或者1-1023）即为真实值，有效数字M不再加上第⼀位的1，⽽是还原为0.xxxxxx的⼩数。这样做是为了表⽰±0，以及接近于0的很⼩的数字。

3. E全为1

255 - 127 = 128 或 2047 - 1023 = 1024， 与第二点相反，这时这个数可能无穷大，所以也特别规定

这时，如果有效数字M全为0，表⽰±⽆穷⼤（正负取决于符号位s）