【蓝桥杯第十二届省赛B】（部分详解）

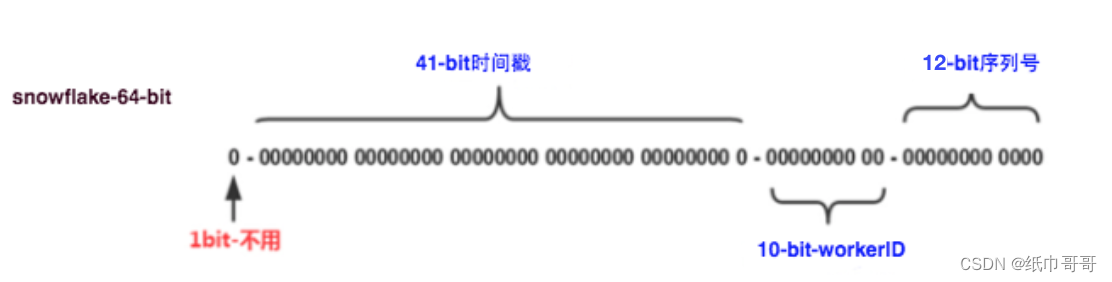
空间

8位1b
1kb=1024b(2^10)
1mb=1024kb(2^20)

时间显示

#include <iostream>
using LL=long long;
using namespace std;
int main()
{
    LL t;
    cin>>t;
    int HH,MM,SS;
    t/=1000;
    SS=t%60;
    //like370000ms=370s,最后360转成分余下10s
    t/=60;
    MM=t%60;
    t/=60;
    HH=t%24;
    printf("%02d:%02d:%02d",HH,MM,SS);
// 请在此输入您的代码
  return 0;
}

上次用02d还是c语言入门的时候，我就说我连门都没入吧（
div（/）本位转换基数，rem(%)高一位转换基数

路径（dp杀我*n）

#include <iostream>
#include<cstring>
using namespace std;
int gcd(int x,int y)
{
    return y==0?x:gcd(y,x%y);
}
int lcm(int x,int y)
{
    return x*y/gcd(x,y);
}
int main()
{
    int dp[2022];
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    memset(dp,0,sizeof(dp));
    for(int i=1;i<=2021;i++)
    {
        for(int j=i+1;j<=i+21;j++)
        {
            if(j>2021)
            break;
            if(dp[j]==0)
            dp[j]=dp[i]+lcm(i,j);
            else
            dp[j]=min(dp[j],dp[i]+lcm(i,j));
        }
           

    } cout << dp[2021] << endl;
    
  // 请在此输入您的代码
  return 0;
}

int f[4]; // 声明一个大小为 4 的整型数组

int dp[4]={0}; 

for (int i = 1; i <= 3; i++)
{
    for (int j = i + 1; j <= i + 2; j++) 
    {
        if (j > 3) 
            break;
        if (dp[j] == 0)
            dp[j] = dp[i] + j * i / gcd(i, j); 
        else
            dp[j] = min(dp[j], dp[i] + j * i / gcd(i, j));
             // 将 f[j] 更新为当前值和新值的较小值
    }
}

cout << f[3] << endl;

当 i = 1 时，j 的范围是 2 到 3。
- 对于 j = 2：
  - f[2] 的初始值为 0，因此计算新值 f[2] = f[1] + 2 * 1 / gcd(1, 2) = 0 + 2 * 1 / 1 = 2，所以 f[2] = 2。
- 对于 j = 3：
  - f[3] 的初始值为 0，因此计算新值 f[3] = f[1] + 3 * 1 / gcd(1, 3) = 0 + 3 * 1 / 1 = 3，所以 f[3] = 3。
当 i = 2 时，j 的范围是 3 到 4。
- 对于 j = 3：
  - f[3] 的当前值为 3，计算新值 f[3] = min(f[3], f[2] + 3 * 2 / gcd(2, 3)) = min(3, 2 + 3 * 2 / 1) = min(3, 8) = 3，所以 f[3] 不变。
- 对于 j = 4：
  - j > 3，因此跳出循环。
最终输出 f[3] 的值，结果为 3。

j循环：在第i个节点可以有的路径有哪些
i循环：上一节点到下一节点的值和当前节点到下一节点的值比较

卡片

#include <iostream>
using LL=long long;
using namespace std;
int main()
{
    LL n;
    cin>>n;
    LL sum=0;
    LL k=1;
    while(sum<n)
    {
        sum+=k;
        k++;
    }
    cout<<k-1;
  // 请在此输入您的代码
  return 0;
}

货物摆放

#include <iostream>
#include<cmath>
using LL=long long;
using namespace std;
LL N=2021041820210418;
LL a[100005];

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    LL cnt=0;
    LL ans=0;
    for(LL i=1;i<=sqrt(N);i++)
    {
        if(N%i==0)
        {
            a[cnt]=i;
            cnt++;
        if (N / i != i)
            {
                a[cnt] = (N / i);
                cnt++;
            }
    }
    }//试了一下，我就说如果不这么算会超时
    for(LL L=0;L<cnt;L++)
        for(LL W=0;W<cnt;W++)
            for(LL H=0;H<cnt;H++)
            {
                if(a[L]*a[W]*a[H]==N)
                {
                    ans++;
                }
            }
    cout<<ans;
  return 0;
}