【频繁模式挖掘】FP-Tree算法（附Python实现）

news2024/7/6 21:00:34

一、实验内容简介

该实验主要使用频繁模式和关联规则进行数据挖掘，在已经使用过Apriori算法挖掘频繁模式后，这次使用FP-tree算法来编写和设计程序，依然使用不同规模的数据集来检验效果，最后分析和探讨实验结果，看其是否达到了理想的效果。本实验依然使用Python语言编写。

二、算法说明

首先简单介绍频繁模式和关联规则：

  • 频繁模式一般是指频繁地出现在数据集中的模式。

  • 关联规则是形如X→Y的蕴涵表达式，其中X和Y是不相交的项集，即X∩Y=∅。关联规则的强度可以用它的支持度（support）和置信度（confidence）来度量。计算公式如下：

  • 支持度：support(A=>B)=P(A∪B)，表示A和B同时出现的概率。

  • 置信度：confidence(A=>B)=support(A∪B)/support(A)，表示A和B同时出现的概率占A出现概率的比值。

  • 强关联规则是指达到了最小支持度和最小置信度的关联规则。

然后再介绍FP-Tree算法：

2000年，Han Jiawei等人提出了基于频繁模式树（Frequent Pattern Tree, FP—Tree）的发现频繁模式的算法FP-Growth。其思想是构造一棵FP-Tree，把数据集中的数据映射到树上，再根据这棵FP-Tree找出所有频繁项集。

FP-Growth算法是指，通过两次扫描事务数据集，把每个事务所包含的频繁项目按其支持度降序压缩存储到FP-Tree中。在以后发现频繁模式的过程中，不需要再扫描事务数据集，而仅在FP-Tree中进行查找即可。通过递归调用FP-Growth的方法可直接产生频繁模式，因此在整个发现过程中也不需产生候选模式。由于只对数据集扫描两次，因此FP-Growth算法克服了Apriori算法中存在的问题，在执行效率上也明显好于Apriori算法。

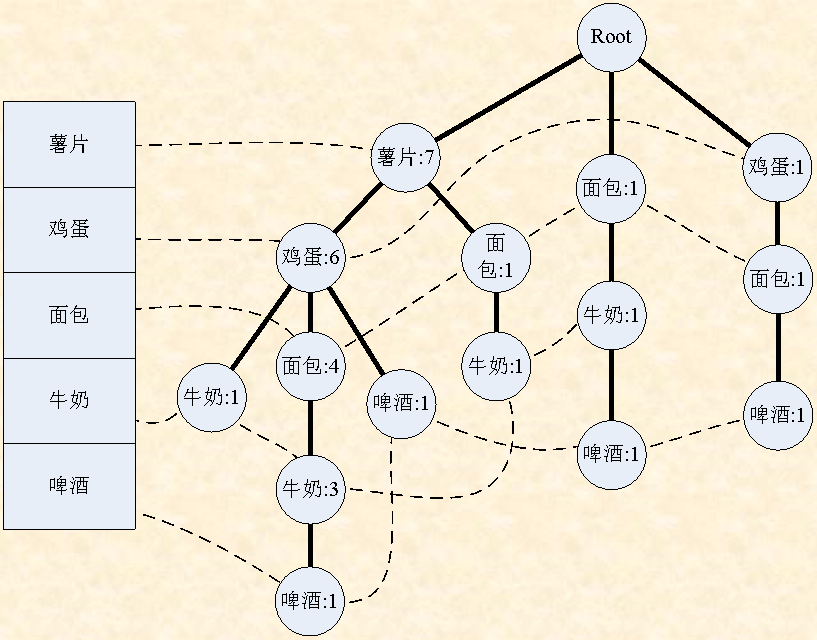
image-20240407103431324

上图为FP-Tree示意图，展示了该数据结构的构成方式。

三、算法分析与设计

了解完算法的基本原理后，现在开始真正实现该算法。首先需要读取最小支持度，读取数据集。这里的数据集可大可小，我用Python中的字典来表示数据

这里的数据存储格式与之前写Apriori算法时一样，使用字典来存储。然后由用户来输入支持度和置信度（因为这次还要挖掘关联规则，所以增加了置信度输入）。

作为FP-Tree的基础，首先构建树节点。一个节点有四个基本属性，分别节点名称、出现次数、双亲节点和孩子节点。因为这里不是二叉树，树的孩子节点个数不确定，因此用字典来存储，大小可控。

class Node:
    def __init__(self, value, parent, count=0):
        self.value = value
        self.parent = parent
        self.count = count
        self.children = {}

    def addChild(self, child):
        self.children.update(child)
    def __init__(self, value, parent, count=0):

前置准备完成后，开始实现FP-Tree算法。FP-Tree算法可大致分为构建项头表、构建FP-Tree、利用条件模式基挖掘频繁模式和关联规则几步。把这几步集成到一个类中，这样避免了大量函数传参操作，思路更清晰。

首先构建项头表，先扫描一遍数据集挖掘频繁1项集，挖掘出来的数据按支持度降序排列，并按此顺序重新排列原数据集的数据，对于不符合要求的数据直接删除。

    def first_scan(self):
        """
        生成项头表，整理数据
        """
        Dict = dict()
        for i in self.data.values():
            for j in i:
                if j not in Dict.keys():
                    Dict.update({j: 1})
                else:
                    Dict[j] += 1
        self.first_list = list(Dict.items())
        self.first_list.sort(key=lambda l: l[1], reverse=True)
        for i in range(len(self.first_list) - 1, 0, -1):
            if self.first_list[i][1] < self.support * len(self.data):
                continue
            else:
                rubbish = [self.first_list[j][0] for j in range(i + 1, len(self.first_list))]
                self.first_list = self.first_list[:i + 1]
                break

        # 将原来的数据重新按支持度排序并剔除非频繁1项集
        sort_refer = [i[0] for i in self.first_list]
        for i in self.data.values():
            for j in i:
                if j in rubbish:
                    i.remove(j)
            i.sort(key=lambda l: sort_refer.index(l))

        # 添加频繁1项集
        self.pinfan.extend([list(i) for i in self.first_list])

        # 整理项头表
        self.value_list = [i[0] for i in self.first_list]
        temp = {}
        for i in self.first_list:
            temp.update({i[0]: []})
        self.first_list = temp

然后构建FP-Tree。这里的过程就比较复杂了，简要说明步骤。第二次遍历数据集，从上往下构建分支，每次若遇到之前没出现的节点，就新建一个新节点，同时更新FP-Tree和项头表，若遇到之前已经出现的节点，则该节点的次数加一。特殊的根节点不需要存储任何数据，只需要存储孩子节点。

    def first_scan(self):
        """
        生成项头表，整理数据
        """
        Dict = dict()
        for i in self.data.values():
            for j in i:
                if j not in Dict.keys():
                    Dict.update({j: 1})
                else:
                    Dict[j] += 1
        self.first_list = list(Dict.items())
        self.first_list.sort(key=lambda l: l[1], reverse=True)
        for i in range(len(self.first_list) - 1, 0, -1):
            if self.first_list[i][1] < self.support * len(self.data):
                continue
            else:
                rubbish = [self.first_list[j][0] for j in range(i + 1, len(self.first_list))]
                self.first_list = self.first_list[:i + 1]
                break

        # 将原来的数据重新按支持度排序并剔除非频繁1项集
        sort_refer = [i[0] for i in self.first_list]
        for i in self.data.values():
            for j in i:
                if j in rubbish:
                    i.remove(j)
            i.sort(key=lambda l: sort_refer.index(l))

        # 添加频繁1项集
        self.pinfan.extend([list(i) for i in self.first_list])

        # 整理项头表
        self.value_list = [i[0] for i in self.first_list]
        temp = {}
        for i in self.first_list:
            temp.update({i[0]: []})
        self.first_list = temp

然后基于FP-Tree同时挖掘频繁模式和关联规则。利用项头表，从支持度低的元素到支持度高的元素，找到该元素在FP-Tree的所有位置，然后自底向上读取其所有祖先节点（除了根节点），同时把出现的次数都改为该元素所对应节点的次数。挖掘出结果后，先剔除掉不满足支持度要求的项，再通过两两组合挖掘出频繁2项集，然后递归挖掘出频繁多项集。同时两两组合算出条件概率与置信度比较，挖掘出1对1的关联规则。

这里涉及到的操作最为复杂，代码量也最大，分了三个方法来实现。

# 详见附录
def find(self):
def cal(self, Dict: dict, delete=False, length=1):
def rules(self, Dict: dict):

四、测试结果

写完代码后，就又到了测试环节。分别测试正确性和性能。在测试性能的时候也会与Apriori算法做比较，以更好地感受到FP-Tree算法的高效性。

首先验证正确性。我使用了教材上的数据集来验证。

img

先给定0.5的支持度和0.75的置信度：

img

经过验证是正确的，再给定0.2的支持度和0.5的置信度：

img

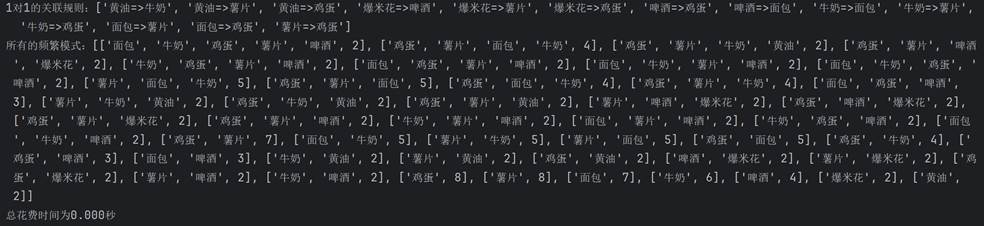
可以看到输出结果大大增加，经过验证也是正确的。

接下来就要扩大数据集的容量了，这样才能分析算法的性能。这里再次使用随机变量来模拟大量的数据：

img

在这里，arr和data2都可以修改，arr可以修改其中的元素来改变权重，data2可以修改数量，这里统一使用0.5作为支持度，0.75作为置信度。

首先用100000的数据来测试：

img

可以看到，一共花了0.288秒。相比其他条件相同下的Apriori算法是1.7秒。

然后把数据量变为1000000来试试：

img

一共花了2.845秒，相比同期Apriori算法一共花了15.58秒。

然后把数据量变为10000000来试试：

img

一共花了28.054秒，相比同期Apriori算法一共花了171.1秒。

最后再把数据量变为一亿，下图是最终结果。

img

差不多跑了8分钟，同期Apriori算法半个小时也没跑出来。可以看出，两个算法所耗费的时间都随时间呈线性增长，但FP-Tree算法显然效率比Apriori算法高得多。

五、分析与探讨

测试完算法后，来分析它的性能，思考FP-Tree算法的优势和缺陷。与Apriori算法相比，FP-Tree算法改进了Apriori算法的I/O瓶颈，巧妙的利用了树结构。Apriori的核心思路是用两个长度为l的频繁项集去构建长度为l+1的频繁项集，而FP-growth则稍有不同。它是将一个长度为l的频繁项集作为前提，筛选出包含这个频繁项集的数据集。用这个数据集构建新的FP-tree，从这个FP-tree当中寻找新的频繁项。如果能找到，那么说明它可以和长度为l的频繁项集构成长度为l+1的频繁项集。然后，我们就重复这个过程。

FP-Tree算法无论从复杂度还是实现难度还是具体技术点来看都比Apriori算法更复杂，但复杂度提高此带来的好处则是更高的效率和更好的性能。二者均为频繁模式挖掘的经典算法，都有必要学习和掌握，期待未来还能不断开发出挖掘频繁模式更加高效的算法。

附录：源代码

# 使用FP-tree实现频繁模式和关联规则挖掘
import itertools
import random
from time import time


# 构建树的节点
class Node:
    def __init__(self, value, parent, count=0):
        self.value = value
        self.parent = parent
        self.count = count
        self.children = {}

    def addChild(self, child):
        self.children.update(child)


# 构建FP-tree
class FP_tree:
    def __init__(self, data, support, confidence):
        self.data = data
        self.first_list = []
        self.value_list = []
        self.support = support
        self.confidence = confidence
        self.tree = None
        self.pinfan = []
        self.rule = []

    def first_scan(self):
        """
        生成项头表，整理数据
        """
        Dict = dict()
        for i in self.data.values():
            for j in i:
                if j not in Dict.keys():
                    Dict.update({j: 1})
                else:
                    Dict[j] += 1
        self.first_list = list(Dict.items())
        self.first_list.sort(key=lambda l: l[1], reverse=True)
        for i in range(len(self.first_list) - 1, 0, -1):
            if self.first_list[i][1] < self.support * len(self.data):
                continue
            else:
                rubbish = [self.first_list[j][0] for j in range(i + 1, len(self.first_list))]
                self.first_list = self.first_list[:i + 1]
                break

        # 将原来的数据重新按支持度排序并剔除非频繁1项集
        sort_refer = [i[0] for i in self.first_list]
        for i in self.data.values():
            for j in i:
                if j in rubbish:
                    i.remove(j)
            i.sort(key=lambda l: sort_refer.index(l))

        # 添加频繁1项集
        self.pinfan.extend([list(i) for i in self.first_list])

        # 整理项头表
        self.value_list = [i[0] for i in self.first_list]
        temp = {}
        for i in self.first_list:
            temp.update({i[0]: []})
        self.first_list = temp

    def build_tree(self):
        """
        建立FP-tree
        :return:fp-tree
        """
        root = Node('root', None)
        parent = root
        for i in self.data.values():
            for j in i:
                # 更新树和项头表
                head = self.first_list
                if j not in parent.children.keys():
                    node = Node(j, parent, 1)
                    temp = {j: node}
                    parent.addChild(temp)
                    head[j].append(node)
                else:
                    parent.children[j].count += 1
                parent = parent.children[j]
            parent = root
        self.tree = root

    def find(self):
        """
        利用建立好的树挖掘频繁模式
        """
        for i in self.value_list[::-1]:
            i_dict = {}
            for j in self.first_list[i]:
                k = j
                count = j.count
                while k != None:
                    if k.value not in i_dict.keys():
                        i_dict[k.value] = count
                    else:
                        i_dict[k.value] += count
                    k = k.parent
            del i_dict['root']
            self.cal(i_dict, True)

    def cal(self, Dict: dict, delete=False, length=1):
        if delete:
            # 预处理，删去支持度低的项
            d = Dict.copy()
            for i, j in d.items():
                if j < self.support * len(self.data):
                    del Dict[i]
        if length == 1:
            self.rules(Dict)
        # 递归挖掘频繁模式
        if length <= len(Dict):
            l = list(Dict.keys())
            pinfan = [l[0], Dict[l[0]]]
            del l[0]
            result = itertools.combinations(l, length)
            for i in result:
                p = pinfan.copy()
                for j in i:
                    p.insert(-1, j)
                    if Dict[j] < p[-1]:
                        p[-1] = Dict[j]
                p[0:-1] = p[-2::-1]
                self.pinfan.append(p)
            self.cal(Dict, length=length + 1)

    def rules(self, Dict: dict):
        """
        只生成1对1的关联规则
        :param Dict:数据源
        """
        if len(Dict) > 1:
            l = list(Dict.keys())
            for i in l[1:]:
                if min(Dict[l[0]], Dict[i]) / Dict[l[0]] > self.confidence:
                    self.rule.append(f"{l[0]}=>{i}")

    def __str__(self):
        """
        输出频繁模式
        :return: 所有的频繁模式
        """
        print("1对1的关联规则：" + str(self.rule))
        self.pinfan.sort(key=lambda l: (len(l), l[-1]), reverse=True)
        return "所有的频繁模式：" + str(self.pinfan)


if __name__ == '__main__':
    data = {1: ['牛奶', '鸡蛋', '面包', '薯片'],
            2: ['鸡蛋', '爆米花', '薯片', '啤酒'],
            3: ['牛奶', '面包', '啤酒'],
            4: ['牛奶', '鸡蛋', '面包', '爆米花', '薯片', '啤酒'],
            5: ['鸡蛋', '面包', '薯片'],
            6: ['鸡蛋', '面包', '啤酒'],
            7: ['牛奶', '面包', '薯片'],
            8: ['牛奶', '鸡蛋', '面包', '黄油', '薯片'],
            9: ['牛奶', '鸡蛋', '黄油', '薯片'],
            10: ['鸡蛋', '薯片']}
    arr = ['牛奶', '面包', '鸡蛋', '馒头', '包子', '饼干']
    support = float(input('请输入最小支持度：'))
    confidence = float(input('请输入最小置信度：'))
    data2 = {i: [random.choice(arr) for j in range(10)] for i in range(100000)}
    begin = time()
    f = FP_tree(data2, support, confidence)
    f.first_scan()
    f.build_tree()
    f.find()
    print(f)
    print("总花费时间为%.3f秒" % (time() - begin))

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1578189.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

HarmonyOS 应用开发-使用colorPicker实现背景跟随主题颜色转换

HarmonyOS 应用开发-使用colorPicker实现背景跟随主题颜色转换

介绍 本示例介绍使用image库以及effectKit库中的colorPicker对目标图片进行取色&#xff0c;将获取的颜色作为背景渐变色&#xff0c;通过swiper组件对图片进行轮播&#xff0c; 效果图预览 使用说明 直接进入页面&#xff0c;对图片进行左右滑动&#xff0c;或者等待几秒&a…
阅读更多...
2014最新AI智能创作系统ChatGPT网站源码+Midjourney绘画网站源码+搭建部署教程文档，支持最近火爆的Suno-v3-AI音乐生成大模型

2014最新AI智能创作系统ChatGPT网站源码+Midjourney绘画网站源码+搭建部署教程文档，支持最近火爆的Suno-v3-AI音乐生成大模型

一、文章前言 SparkAi创作系统是基于ChatGPT进行开发的Ai智能问答系统和Midjourney绘画系统&#xff0c;支持OpenAI-GPT全模型国内AI全模型。本期针对源码系统整体测试下来非常完美&#xff0c;那么如何搭建部署AI创作ChatGPT&#xff1f;小编这里写一个详细图文教程吧。已支持…
阅读更多...
鼠标经过切换项，切换显示对应的内容（js）

鼠标经过切换项，切换显示对应的内容（js）

一、功能描述 有多个切换项&#xff0c;鼠标移到每一项时对应切换下面对应的内容&#xff0c;一项对应一项内容&#xff0c;并且切换选中的样式。 二、实现效果 以这个例子为例。 三、实现思路 1.获取所有切换项。 2.获取所有切换项内容。 3.定义好“move”样式&#xff0…
阅读更多...
链表之双向链表的实现

链表之双向链表的实现

铁汁们大家好&#xff0c;我们上一篇博客学习了单链表&#xff0c;这节课让我们继续往深学习&#xff0c;学习一下双线链表&#xff0c;话不多说&#xff0c;我们开始吧&#xff01; 目录 1.双向链表 2.顺序表和链表的优缺点 3.双向链表的实现 1.双向链表 1.我们要实现的双线…
阅读更多...
IDEA中修改git的作者、邮箱名称

IDEA中修改git的作者、邮箱名称

目录 一、查看当前git信息 1、查看git作者名称 如下图&#xff1a; 2、查看git邮箱信息 二、修改git信息 1、修改git作者名称 如下图&#xff1a; 2、修改git邮箱名称 一、查看当前git信息 1、查看git作者名称 在git控制台 或者 Terminal 输入 git config user.name …
阅读更多...
蓝桥杯物联网竞赛_STM32L071_16_EEPROM

蓝桥杯物联网竞赛_STM32L071_16_EEPROM

仍然是没有考过的知识点 朴素的讲就是板子中一块不会因为断电重启而导致数值初始化的一片地址 要注意的是有时候容易把板子什么写错导致板子什么地址写坏了导致程序无法烧录&#xff0c;这个时候记得一直按flash键烧录&#xff0c;烧录时会报错&#xff0c;点击确定&#xff0…
阅读更多...
飞鸟写作可靠吗 #职场发展#经验分享#经验分享

飞鸟写作可靠吗 #职场发展#经验分享#经验分享

飞鸟写作是一个非常便捷的论文写作工具&#xff0c;不仅可以帮助用户高效地完成论文写作&#xff0c;还可以提供查重降重的功能&#xff0c;帮助用户确保论文的原创性。那么&#xff0c;飞鸟写作到底可靠吗&#xff1f;答案是肯定的。 首先&#xff0c;飞鸟写作提供的查重降重功…
阅读更多...
经典算法-分治法由散点得出凸包-python实现

经典算法-分治法由散点得出凸包-python实现

import copy import random import matplotlib import mathdef distance_p2l(point, line_point1, line_point2):if (line_point2[0] - line_point1[0]) 0:return abs(point[0] - line_point2[0])# 计算直线的斜率m (line_point2[1] - line_point1[1]) / (line_point2[0] - l…
阅读更多...
电脑出现mfc140u.dll丢失怎么办？教你7个方法解决此问题

电脑出现mfc140u.dll丢失怎么办？教你7个方法解决此问题

mfc140u.dll 是一个动态链接库 (Dynamic Link Library, DLL) 文件&#xff0c;它是 Microsoft Windows 操作系统环境下用于支持应用程序运行的重要组成部分。具体来说&#xff0c;mfc140u.dll 是 Microsoft Foundation Class (MFC) 库 14.0 版本的 Unicode 版本动态链接库文件。…
阅读更多...
分享一下项目中遇到的排序失效问题

分享一下项目中遇到的排序失效问题

今天把原来的一个查询接口的业务代码进行了优化&#xff0c;减少了十几行冗余的代码。 原来的代码 ChongwuServiceImpl.java /*** author heyunlin* version 1.0*/ Slf4j Service public class ChongwuServiceImpl implements ChongwuService {Overridepublic JsonResult<…
阅读更多...
TensorFlow-gpu安装教程(Linux系统）

TensorFlow-gpu安装教程(Linux系统）

一、TensorFlow-gpu环境的安装 使用这个代码安装的前提是你的深度学习已经环境存在 &#xff08;例如&#xff1a;conda、pytorch、cuda、cudnn等环境&#xff09; TensorFlow版本对应GPU版本&#xff0c;自己选择版本&#xff0c;也可以忽略版本直接安装TensorFlow-gpu cond…
阅读更多...
百度松果菁英班——机器学习实践五：明星图片爬取

百度松果菁英班——机器学习实践五：明星图片爬取

飞桨AI Studio星河社区-人工智能学习与实训社区 &#x1f96a;图片爬取 import requests import os import urllib ​ class GetImage():def __init__(self,keyword大雁,paginator1):# self.url: 链接头self.url http://image.baidu.com/search/acjson?self.headers {User…
阅读更多...
IO_DAY7

IO_DAY7

1:实现2个终端之间的互相聊天 要求:千万不要做出来2个终端之间的消息发送是读一写的&#xff0c;一定要能够做到&#xff0c;一个终端发送n条消息&#xff0c;另一个终端一条消息都不回复都是没有问题的 终端A&#xff1a; #include<myhead.h> int main(int argc, char…
阅读更多...
测开面经（pytest测试案例，接口断言，多并发断言）

测开面经（pytest测试案例，接口断言，多并发断言）

pytest对用户登录接口进行自动化脚本设计 a. 创建一个名为"test_login.py"的测试文件&#xff0c;编写以下测试脚本 import pytest import requests# 测试用例1&#xff1a;验证登录成功的情况 # 第一个测试用例验证登录成功的情况&#xff0c;发送有效的用户名和密…
阅读更多...
three.js零基础入门超全超细的教程整理（一）

three.js零基础入门超全超细的教程整理（一）

事情是这样的&#xff1a; 有一天 我干完活 看技术文章 发现了three.js 诶&#xff01;这玩应挺有意思 盘盘 于是第一天找教程 上官网 初上手 第二天 找案例 渲模型 试VR 第三天 捋文档 然后来活了 没时间捋了 下面是集百家精华教程的整理总结 涉及到教程方面有加源作者和地址…
阅读更多...
AI智能分析盒子在工地的应用，提高工地管理效率和安全性

AI智能分析盒子在工地的应用，提高工地管理效率和安全性

工地ai智能分析盒子是一种基于人工智能视觉分析技术的人工智能盒子&#xff0c;旨在提升工地作业区域的管理效率和保障作业人员的安全。通过最前沿的AI视觉算法、大数据&#xff0c;能够实时监控工地现场视频流画面&#xff0c;对施工工地人员的工作着装及日常作业行为进行规范…
阅读更多...
【多线程】进程（进程的概念+进程的管理+PCB（进程控制块）+进程的调度）

【多线程】进程（进程的概念+进程的管理+PCB（进程控制块）+进程的调度）

文章目录 进程一、计算机的组成&#xff1a;1.指令&#xff08;Instruction&#xff09; 二、浅谈操作系统1.日常的操作系统1.操作系统内核内核&#xff1a;进程的隔离性&#xff1a; 三、进程&#xff08;process&#xff09;1.进程的概念2.进程的管理1.管理的两个角度&#x…
阅读更多...
短视频有效粉丝不够怎么涨？有效粉丝不满足500怎么解决？不够500有效粉丝怎么挂橱窗？

短视频有效粉丝不够怎么涨？有效粉丝不满足500怎么解决？不够500有效粉丝怎么挂橱窗？

在这个流量主导的短视频时代&#xff0c;想要在短视频平台上增加粉丝数量并非易事。然而随着短视频平台规则更新4月16日开始&#xff0c;不能满足五百有效粉丝&#xff0c;就不能挂橱窗了&#xff0c;对一些有效粉丝不够的用户来说&#xff0c;这个的确是有点麻烦&#xff0c;而…
阅读更多...
Mysql底层原理二：Buffer Pool

Mysql底层原理二：Buffer Pool

1.数据区 就是描述信息缓存页这块&#xff0c;用来存放从磁盘加载的数据页&#xff08;看上图 索引页和数据页是分开的&#xff09; 2. free链表 用来标识数据区哪些数据页是可用的 3. flush链表 update的时候&#xff0c;如果数据在数据区可以找到&#xff0c;那就直接内…
阅读更多...
基于Vue3 中后台管理系统框架

基于Vue3 中后台管理系统框架

基于Vue3 中后台管理系统框架 文章目录 基于Vue3 中后台管理系统框架一、特点二、源码下载地址 一款开箱即用的 Vue 中后台管理系统框架&#xff0c;支持多款 UI 组件库&#xff0c;兼容PC、移动端。vue-admin, vue-element-admin, vue后台, 后台系统, 后台框架, 管理后台, 管理…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023