系列文章目录
第二章 主色提取之颜色空间转化
目录
系列文章目录
文章目录
前言
一、HSV 和 RGB 颜色空间
二、颜色转化
1. RGB to HSV
2. HSV to RGB
三、 完整代码
前言
HSV 颜色空间和 RGB 颜色空间的转化。
一、HSV 和 RGB 颜色空间
RGB颜色使用的最多，分别为红色(R)，绿色(G)和蓝色(B)。
HSV颜色中的 H( hue) 表示色 调，由颜色名称来辨别，如红、橙、绿，它用角度度量，从-180° 到 180°，或从 0°到 360°; S( saturation) 表示色度或饱和度，指颜色 的深浅，例如同 样 是 红 色，也会因浓度不同分为深红和浅红，S 用百分比来度量，从 0% 到完全饱和的 100% ; V( value) 表示亮 度，指颜色的明暗程度，通常用百分比来度量，从黑 0% 到白100% 。
二、颜色转化
1. RGB to HSV
RGB 到 HSV 还是比较简单实现的，
在计算公式前，有三个假设：
- 设 (r, g, b) 的值是在 0 到 1 之间的实数
- 设 max 等于 r, g, b 中的最大者
- 设 min 等于 r, g, b 中的最小者
公式如下图：
代码如下：
def RGB2HSV(r,g,b):
r, g, b = r / 255, g / 255, b / 255
ma = max(r, g, b)
mi = min(r, g, b)
diff = ma - mi
if ma == mi:
h = 0
elif ma == r and g >= b:
h = 60 * ((g - b)/diff) + 0
elif ma == r and g < b:
h = 60 * ((g - b)/diff) + 360
elif ma == g:
h = 60 * ((b - r)/diff) + 120
elif ma == b:
h = 60 * ((r - g)/diff) + 240
if ma == 0:
s = 0
else:
s = diff / ma
v = ma
return h, s, v
2. HSV to RGB
HSV 转化为 RGB 相对于上面来说是要难一些的，
要注意两点：
1 参数输入范围 h(0~360), s(0~100), v(0~100)，所以要把 s, v 缩放到0~1之间
2 转换结果R(0~100),G(0~100),B(0~100)
公式如下：
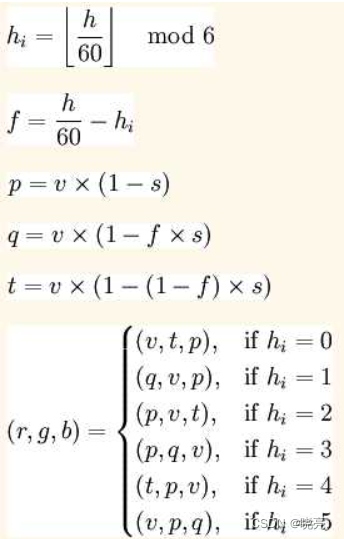
实现代码如下：
def HSV2RGB(h, s, v):
s, v = s / 100, v /100
i = round(h / 60) % 6
f = (h / 60) - i
p = v * (1 - s)
q = v * (1 - f * s)
t = v * (1 - (1 - f) * s)
R, G, B = 0, 0, 0
if i == 0:
R, G, B = v, t, p
elif i == 1:
R, G, B = q, v, p
elif i == 2:
R, G, B = p, v, t
elif i == 3:
R, G, B = p, q, v
elif i == 4:
R, G, B = t, p, v
elif i == 5:
R, G, B = v, p, q
r, g, b = round(R * 255), round(G * 255), round(B * 255)
return r, g, b
三、 完整代码
完整代码可以在GitHub上下载，如果感兴趣，不妨给我个星呀，哈哈。
连接：GitHub - Liangliangb/Image-main-color-extraction: Use the k-means algorithm to extract the dominant color of the picture.Use the k-means algorithm to extract the dominant color of the picture. - GitHub - Liangliangb/Image-main-color-extraction: Use the k-means algorithm to extract the dominant color of the picture.
https://github.com/Liangliangb/Image-main-color-extraction.git
