题目

只有 所有 节点能够形成且 只 形成 一颗 有效的二叉树时，返回 true；否则返回 false。

如果节点 i 没有左子节点，那么 leftChild[i] 就等于 -1。右子节点也符合该规则。

注意：节点没有值，本问题中仅仅使用节点编号。

 

示例 1：

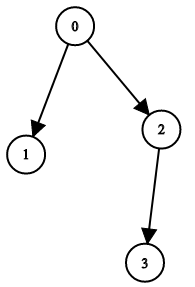
输入：n = 4, leftChild = [1,-1,3,-1], rightChild = [2,-1,-1,-1]
输出：true

示例 2：

输入：n = 4, leftChild = [1,-1,3,-1], rightChild = [2,3,-1,-1]
输出：false

示例 3：

输入：n = 2, leftChild = [1,0], rightChild = [-1,-1]
输出：false

示例 4：

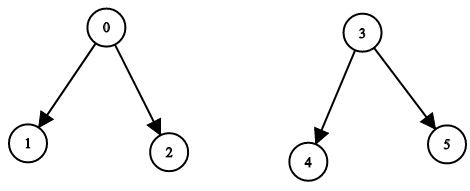
输入：n = 6, leftChild = [1,-1,-1,4,-1,-1], rightChild = [2,-1,-1,5,-1,-1]
输出：false

 

提示：

• 1 <= n <= 10^4
• leftChild.length == rightChild.length == n
• -1 <= leftChild[i], rightChild[i] <= n - 1

思路

看题目和例子总结

• 二叉树
• 一个节点存在一个以上的父节点 return false
• 闭环 return false
• 一个以上的联通量, return false

使用并查集可以解决上面2-4点情况。

• 第二种情况
  在union的时候判断一下节点是否已经关联了父节点就行了
• 第三种情况。
  find一下父子节点的根节点，判断是否相等就可以知道父子节点是否存在闭环
• 第四种情况。
  统计一下执行union的次数，就可以知道只剩下多少个联通量。

代码

class Solution {

    int ans;

    public boolean validateBinaryTreeNodes(int n, int[] leftChild, int[] rightChild) {
        int[] fa = new int[n];
        ans = n;
        for (int i = 0; i < n; ++i) fa[i] = i;
        for (int i = 0; i < n; ++i) {
            if (union(fa, i, leftChild[i]) || union(fa, i, rightChild[i])) return false;
        }
        if (ans > 1) return false;
        return true;
    }

    public int find(int[] fa, int n) {
        return fa[n] == n ? n : find(fa, fa[n]);
    }
    public boolean union(int[] fa, int f, int c) {
        if (c == -1) return false;
        if (fa[c] != c) return true;
        int a = find(fa, f), b = find(fa, c);
        if (a == b) return true;
        fa[b] = a;
        ans--;
        return false;
    }
}