343.整数拆分

动规五步：

1. 确定 dp[i] 含义：拆分数字 i，可以获得的最大乘积为 dp[i]。
2. 递推公式：dp[i] = max(j * (i - j), j * dp[i - j])。i 可以被拆解为两个数（j 和 i - j）或者多个数（j 和 dp[i - j]），因为根据我们的 dp定义，这里的 dp[i - j] 意思为 拆分数字 i - j。
3. dp数字初始化：题目要求 n >= 2，而我们知道拆分 2，最大乘积为 1*1 = dp[2]。
4. 遍历顺序：从左至右，因为 dp[i] 需要用到 dp[i-j]。
5. 打印dp数组

class Solution:
    def integerBreak(self, n: int) -> int:
        # 我们使用下标表示数字的大小，
        # dp数组需要存储 0 到 n 共 n+1 个数字
        dp = [0] * (n + 1)
        dp[2] = 1 * 1
        
        for i in range(3, n + 1):
            for j in range(1, i):
                # 对于每个 j，都会更新一个 dp[i]，需要其中最大的 dp[i]
                dp[i] = max(dp[i], max(j * (i - j), j * dp[i - j]))
        return dp[n]

96.不同的二叉搜索树

我们可以画出 n = 1, 2, 3的情况，找出规律，如下图：

 

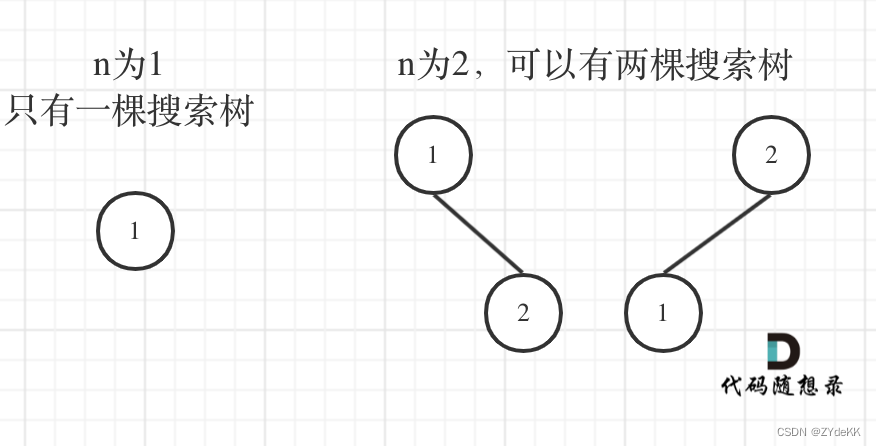
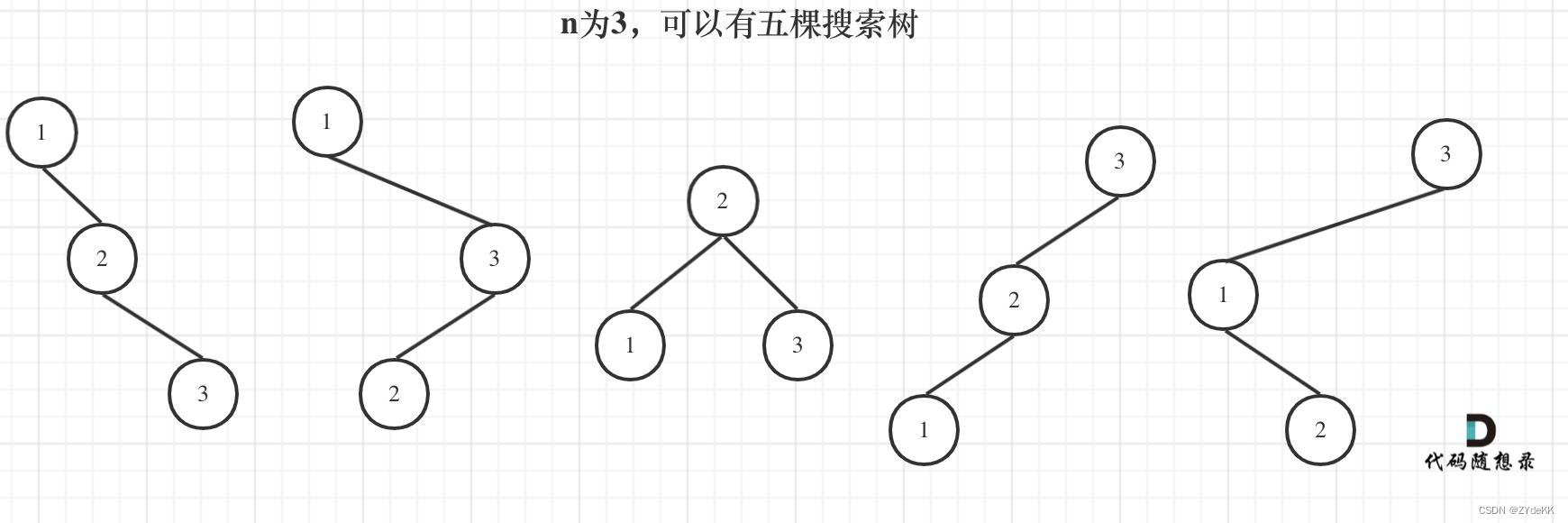
在 n = 3 的时候：

• 若根节点为1，根据二叉搜索树的性质，左子树没有节点，右子树2个节点，其右子树的情况与 n = 2 的时候一样。
• 若根节点为3，根据二叉搜索树的性质，左子树2个节点，右子树没有节点，其左树的情况与 n = 2 的时候一样。
• 若根节点为2，根据二叉搜索树的性质，左子树1个节点，右子树1个节点，其左右子树的情况与 n = 1 的时候一样。

因此，dp[3] = 以1为头节点的搜索树数量 + 以2为头节点的搜索树数量 + 以3为头节点的搜索树数量。

• 1为头节点的搜索树数量 = 左子树有0个节点的搜索树数量 * 右子树有2个节点的搜索树数量
• 2为头节点的搜索树数量 = 左子树有1个节点的搜索树数量 * 右子树有1个节点的搜索树数量
• 3为头节点的搜索树数量 = 左子树有2个节点的搜索树数量 * 右子树有0个节点的搜索树数量

有2个元素的搜索树数量就是dp[2]。

有1个元素的搜索树数量就是dp[1]。

有0个元素的搜索树数量就是dp[0]。

所以dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]

动规五步曲：

1. dp数组的含义：由1到i为节点组成的二叉搜索树的个数为 dp[i]。
2. 递推公式：dp[i] += dp[j - 1] * dp[i - j]。1 到 i 为头节点的所有搜索树之和。假设用 j 来遍历，以 j 为头节点的搜索树中，左子树有 j - 1 个节点，右子树有 i - j 个节点。
3. 初始化：dp[0] = 1。如果只有一个节点，其也是一个二叉搜索树，因此 dp[1] = 1。根据递推公式：dp[1] = dp[1 - 1] * dp[1 - 1] = dp[0] * dp[0] ，因此虽然 dp[0] 没有意义，但必须初始化为 1。
4. 遍历顺序：dp[i] 由小于 i 的节点得出，因此从小到大。
5. 打印dp数组

class Solution:
    def numTrees(self, n: int) -> int:
        # 如果我们显式初始化 dp[1] = 1，则会报错。
        # dp[1] 依赖下方的代码来更新，必须保持 dp[1]被初始化为0
        dp = [0] * (n + 1)
        dp[0] = 1
        
        for i in range(1, n + 1):
            for j in range(1, i + 1):
                dp[i] += dp[j - 1] * dp[i - j]
        
        return dp[n]