目录
一、什么是数字电路? (Digital Circuit )
1.概念
2.分类
3.优点
4.数电与模电的区别
二、数制 (十进制:Decimal)
1.概述
2.进位制
3.基数
4.位权
5.二进制的算术运算
三、编码 (二进制:Binary )
1.什么是原码、反码和补码?
2.常见的编码
3.格雷码(Gray Code)
4.奇偶校验码
五、常用进制间的转换
1.十进制(Decimal) - 二进制(Binary)
2.二进制(Binary) - 十六进制(Hexadecimal)
3.二进制(Binary) - 八进制(Octal)编辑
4.十进制(Decimal) - 八进制(Octal) - 十六进制(Hexadecimal)编辑
六、逻辑代数的基本运算规律
1.基本运算定律
2.常用恒等式
七、逻辑代数的基本定理
1.代入定理
2.反演定理
3.对偶定理
八、逻辑函数(Logic Function)
1.逻辑函数概述
2.逻辑函数的描述方法
3.逻辑真值表
4.逻辑函数式
5.逻辑图
6.波形图(Waveform)
7.卡诺图
8.硬件描述语言(HDL)
9.逻辑函数的公式化简法
九、逻辑函数的两种标准形式
1.最小项
2.最大项
十、卡诺图化简法
一、什么是数字电路? (Digital Circuit )
1.概念
用数字信号完成对数字量进行算术运算和逻辑运算的电路称为数字电路, 或数字系统。由于它具有逻辑运算和逻辑处理功能,所以又称数字逻辑电路。
2.分类

3.优点
- 稳定性好,可靠性高
- 可长期存储
- 便于计算机处理
- 便于高度集成化
4.数电与模电的区别
工作任务不同:
- 模电研究的输出与输入信号的大小、相位、失真等的关系。
- 数字电路主要研究的是输出与输入间的逻辑关系。
三极管的工作状态不同:
- 模电主要工作在放大区。
- 数字电路中的三极管工作在饱和或截止状态,起开关作用。


二、数制 (十进制:Decimal)
1.概述
数字电路所处理的各种数字信号都是以数码形式给出的,用数码表示数量的大小时, 采用的各种计数进位制规则称为数制。
2.进位制
多位数码每一位的构成以及从低位到高位的进位规则。
3.基数
数制所使用数码的个数。
4.位权
在某一进位制的数中,每一位的大小都对应着该位上的数码乘上一个固定的数,这个固定的数就是这一位的权数,权数是一个幂。

5.二进制的算术运算
当两个二进制数码表示两个数量大小时,他们之间可以进行数值运算,这种运算称为算术运算

三、编码 (二进制:Binary )
概念:用二进制数表示各种数字或符号的过程称为编码。
1.什么是原码、反码和补码?
- 正数的反码和补码不变。
- 负数的反码与原码相反(头位0表示正数,1表示负数),补码在反码基础上加一。

2.常见的编码
2421BCD,5421BCD 和 8421BCD码
余三码是在8421BCD码基础数加3

3.格雷码(Gray Code)
两个相邻代码之间仅有 1 位数码不同的无权码称为格雷码。
优点:
功耗低,速度快,出错几率小。
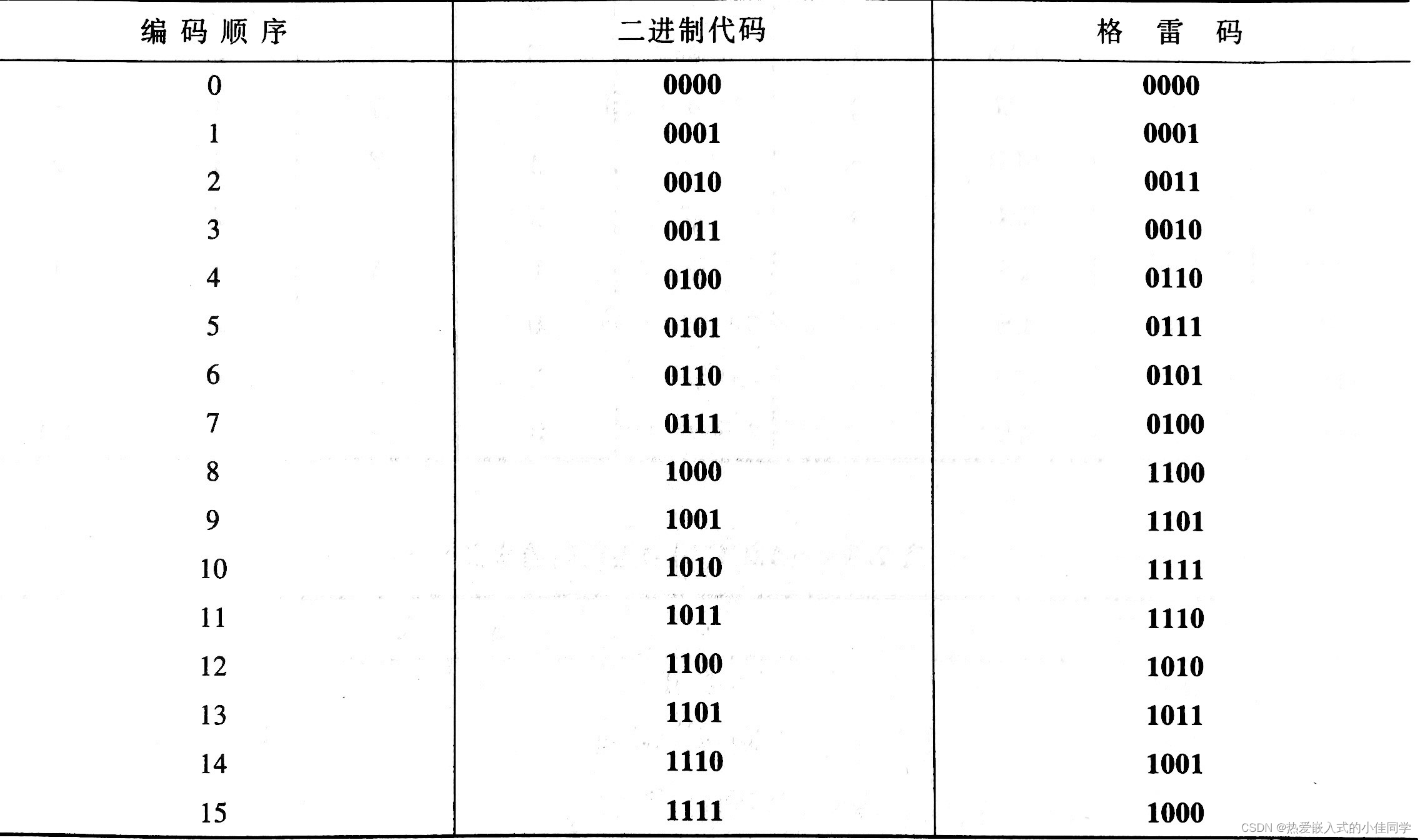
4.奇偶校验码
- 1的个数为奇数的话最后一位为0
- 1的个数为偶数的话最后一位为0

五、常用进制间的转换
1.十进制(Decimal) - 二进制(Binary)


2.二进制(Binary) - 十六进制(Hexadecimal)


3.二进制(Binary) - 八进制(Octal)

4.十进制(Decimal) - 八进制(Octal) - 十六进制(Hexadecimal)

六、逻辑代数的基本运算规律
1.基本运算定律
01定律

重叠律

互补律

交换律

结合律

分配律

反演律(摩根定律)

否定率(非非律)

2.常用恒等式
吸收定理
当两个乘积项相加时,若其中一项是另一项的因子,则另一项是多余的,可以消去

当两个乘积项相加时,如果一项取反后是另一项的因子, 则此因子是多余的,可以消去

当两个乘积项相加时,若他们分别包含B和B'两个因子,而其他因子相同, 则两项定能合并,且可将B和B'两个因子消去

变量A和包含A的和相乘时,其结果等于A,即可将和消掉

多余项定理
若两个乘积项中分别包含A和A'两个因子,而这两个乘积项的其余因子组成 第三个乘积项时,则第三个乘积项是多余的,可以消去。

七、逻辑代数的基本定理
1.代入定理
在任何一个包含变量A的逻辑等式中,若以另外一个逻辑式代入式中所有A的位置,则等式仍然成立
用途:
在等式中导出新的公式

2.反演定理
对于任意一个逻辑式Y,若将其中所有的“·”换成“+”,“+”换成“·”, 0换成1,1换成0.原变量换成反变量,反变量换成原变量,则得到的结果就是Y'
用途:
求逻辑函数的反函数


3.对偶定理
若两逻辑式相等,则他们的对偶式也相等
对偶式定义:对于任何一个逻辑试Y,若将其中所有的“·”换成“+”,“+”换成“·”, 0换成1,1换成0.则得到一个新的逻辑试Y*,Y*就成为Y的对偶式
用途:可以导出新的公式,且使要证明的公式减少一半。


八、逻辑函数(Logic Function)
1.逻辑函数概述
以逻辑变量作为输入,运算结果作为输出,当输入的变量取值确定后,输出 的取值也随之确定,这种函数关系称为逻辑函数。写作Y=F(A,B,C,……) 由于变量和输出的取值只有0和1两种状态,所以我们所讨论的都是二值逻辑函数
2.逻辑函数的描述方法
- 逻辑真值表
- 逻辑函数式
- 逻辑图
- 波形图
- 卡诺图
- 硬件描述语言
3.逻辑真值表
將输入变量所有的取值下对应的输出值找出来,列成表格,例如:


4.逻辑函数式
將输出与输入之间的关系写成与、或、非等运算的组合式

5.逻辑图
將逻辑函数中的各变量之间的与、或、非等逻辑关系用图形符号表示出来

6.波形图(Waveform)
将逻辑函数输入变量每一种可能出现的取值与对应的 输出值按时间顺序依次排列起来,也称时序图(Timing Diagram)

7.卡诺图
由美国工程师卡诺(M.Karnaugh)首先提出的,所以将这种图形称为卡诺图

8.硬件描述语言(HDL)
设计人员利用EDA工具描述电子电路的一种方法


9.逻辑函数的公式化简法
在与或逻辑函数式中,若其中包含的乘积项已经很少,而且每个乘积项里的因子也不能再减少时,则称此逻辑函数式为最简形式。
化简逻辑函数的目的就是消去多余乘积项和每个乘积项中多余的因子,以得到最简形式。





九、逻辑函数的两种标准形式
1.最小项
在n变量逻辑函数中,若m为包含n的因子的乘积项,而且这n个变量均以原变量或反变量的形式在m中出现1次,则称m为该组变量的最小项,输入变量的每一组取值都是一个对应的。

重要性质
- 输入变量的任何取值下必有一个最小项,而且仅有1个最小项的值为1
- 全体最小项之和为1
- 任意两个最小项的乘积为0
- 具有相邻的两个最小项之和可以合并成一项并消去一对因子
2.最大项
在n变量逻辑函数中,若M为n个变量之和,而且这n个变量均以原变量或反变量的形式在M中出现1次,则称M为该组变量的最大项。

主要性质
- 输入变量的任何取值下必有一个最大项,而且仅有1个最大项的值为0
- 全体最大项之积为0
- 任意两个最大项之和为1
- 具有1个变量不同的两个最大项的乘积等于各相同变量之和
最小项之和形式:
先将函数化为若干乘积之和的形式,也叫“积之和”简称SOP。
然后利用 A+A'=1将每个乘积项缺少的因子补全,这样可将与或形式化为最小项之和的标准形式。
应用:逻辑函数的化简,计算机辅助分析和设计


最大项之积:先将函数化为若干乘积之和的形式,再利用AA'=0将每个多项式中缺少的变量补齐,就可以将函数式的或与形式化成最大项之积的形式。
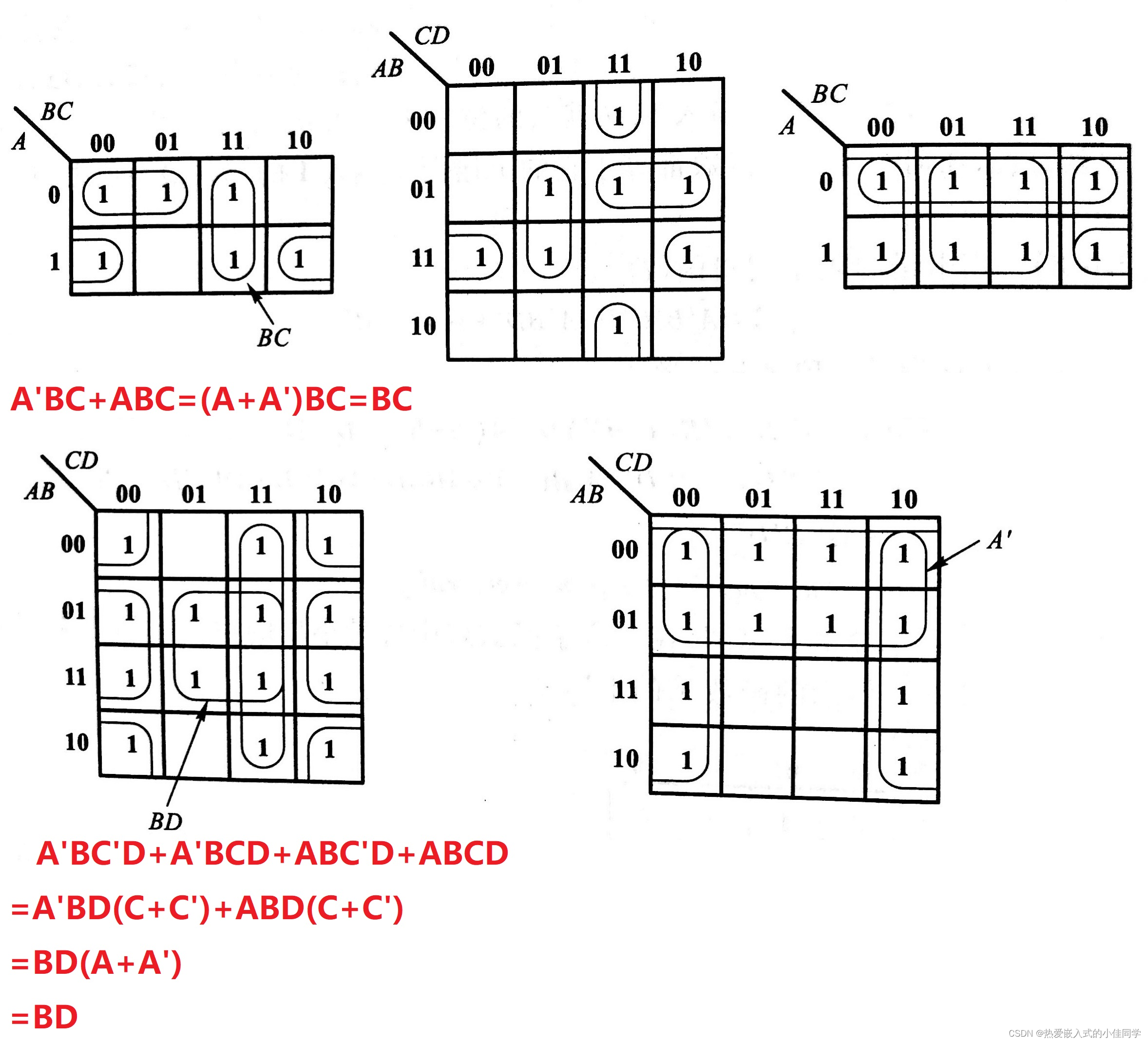
十、卡诺图化简法
将n变量的全部最小项各用一个小方块表示,并使具有逻辑相邻性的最小项在几何位置上也相邻地排列起来,所得到的图形称为n变量最小项的卡诺图。


用卡诺图表示逻辑函数:
先将逻辑函数化为最小项之和的形式,然后再卡 诺图上与这些最小项对应的位置上填入1,在其余的位置上填入0。


卡诺图化简逻辑函数原理:
利用具有相邻的最小项可以合并,并消去不同的因子。 由于卡诺图几何位置相邻与逻辑相邻是一致的,所以可直观的找出具有相邻性的最小项并合并化简。
化简步骤:
- 1.将函数化为最小项之和的形式
- 2.画出表示该逻辑函数的卡诺图
- 3.找出可以合并的最小项
- 4.选取化简后的乘积项
选取原则:
- 1.这些乘积项应包含函数式中所有的最小项(应覆盖卡诺图中的所有的1)
- 2.所用的乘积项数目最少,也就是可合并的最小项组成的矩形组数最少
- 3.每个乘积项包含的因子最少(每个可合并的最小项矩形包含尽量多的最小项)








![【PyTorch][chapter 25][李宏毅深度学习][Transfer Learning-1]](https://img-blog.csdnimg.cn/direct/d5d899d446d8499a83839a2eef7611e9.png)