Dijkstra 算法
Dijkstra 算法与BFS算法的区别就是 : 从容器中弹出接下来要访问的节点的规则不同
BFS 弹出: 层级最浅的原则,队列里最下方的元素
Dijkstra 弹出: 代价最小的节点g(n)
g(n) :表示的是从开始节点到当前n节点的代价累加
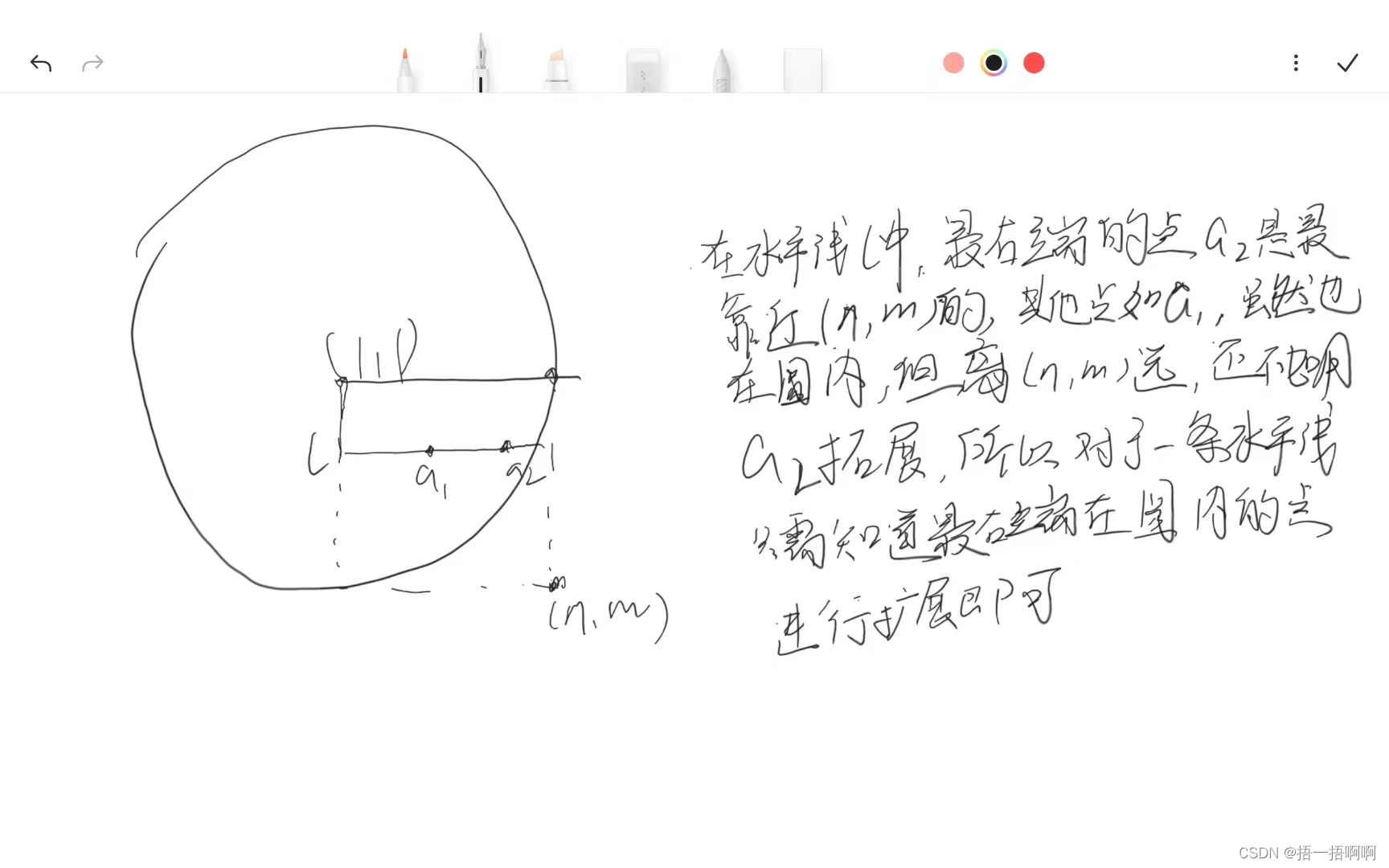
Dijkstra在扩展的时候,同时考虑从n节点扩展所有可扩展节点的代价g(),如果某个节点m的代价g(m)比g(n)要小,则更新当前代价为g(m)
Dijkstra的最优性保证:图运行的过程中,任何一个被扩展或者访问的节点,保证存储的代价g()值是从起点节点开始到当前节点的最小值

Dijkstra 算法 伪代码流程
维护一个优先级队列,存储所有被扩展的节点,且节点按g()值的大小自动按从小到大排列。
-优先级队列首先为空,以起始节点Xs进行初始化
-起始节点g(Xs)=0,并且初始化其它节点的代价为无穷大
-循环:
1、如果队列是空的,返回false,跳出循环
2、弹出优先级队列中代价最小的节点n
3、标记节点n为被扩展节点
4、如果节点n为目标节点,返回true,跳出循环
5、找到n节点周围可以扩展的所以节点(没被扩展过)m
6、进行判断 如果g(m)为无穷大(说明其它节点也没发现过m),
7、则计算 真正的g(m)=g(n)+Cnm,然后将m节点加入到优先级队列中
8、进行判断 如果g(m)不为无穷大,有值了(说明其它节点发现过m,m已经在优先级队列中)
9、再次进行判断 如果之前发现m时计算的g(m)比g(n)+Cnm大的话
10、更新g(m)=g(n)+Cnm。
11、重复循环至步骤1
-结束循环
Dijkstra 算法步骤示例
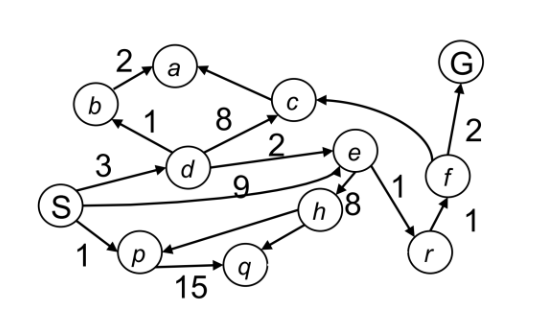
以这个图将Dijkstra 算法运行的步骤进行一个示例:
1、首先初始化队列,将起始节点放入优先级队列中

2、弹出起始节点
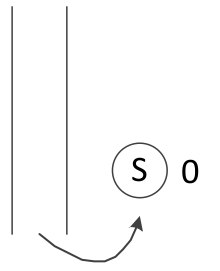
3、扩展弹出节点周围的节点
起始节点S可以扩展到子节点d\e\p,并且计算各节点的g值
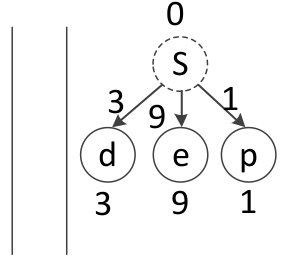
4、将扩展的节点加入到优先级队列中,并且进行排序
g(p)最小,放到队列最前面,也就是图中的最下面,然后是d,最后是e。

5、弹出最小的g值节点
也就是p节点

然后循环至步骤3,直至结束
Dijkstra算法的优劣分析
- 优点:完备的(如果问题有解,一定能找到解);最优的(找到的解一定是最优的)
- 缺点:没有目标终点方向的,只是比广度搜索多了一个代价值判断,如果每个边的代价都是1的话,那么就变成了广度搜索。
针对该缺点,与之对应的就是启发式搜索,例如贪心算法,根据到目标的进行一个启发式搜索。
如果Dijkstra的最优性与启发式搜索结合,使搜索具有方向性时,也就是 A*算法了。
A*算法
A_算法与Dijkstra算法的框架是完全一样的,**A_算法就是有启发性的Dijkstra算法**
代价函数:g(n) 表示的是从开始节点到当前n节点的代价累加
启发函数:h(n) 表示当前节点到目标节点估计所花的代价
优先级队列:维护的是 代价函数+启发函数的 节点从小到大排序 f(n)=g(n)+h(n)
每次弹出的节点就是最小的f(n)值的节点。
A*算法伪代码
维护一个优先级队列,存储所有被扩展的节点,且节点按f()值的大小自动按从小到大排列。
-所以节点的启发值h(n)是为被定义的,是不知道的,到具体的节点再计算
-优先级队列首先为空,以起始节点Xs进行初始化
-起始节点g(Xs)=0,并且初始化其它节点的代价为无穷大
-循环:
1、如果队列是空的,返回false,跳出循环
2、**弹出优先级队列中f(n)最小的节点n** [唯一与djikstra不同的地方]
3、标记节点n为被扩展节点
4、如果节点n为目标节点,返回true,跳出循环
5、找到n节点周围可以扩展的所以节点(没被扩展过)m
6、进行判断 如果g(m)为无穷大(说明其它节点也没发现过m),
7、则计算 真正的g(m)=g(n)+Cnm,然后将m节点加入到优先级队列中
8、进行判断 如果g(m)不为无穷大,有值了(说明其它节点发现过m,m已经在优先级队列中)
9、再次进行判断 如果之前发现m时计算的g(m)比g(n)+Cnm大的话
10、更新g(m)=g(n)+Cnm。
11、重复循环至步骤1
-结束循环
A* 算法步骤示例
下面是一个A_算法的演示图,每个边有个预先设置的代价g,每个节点有提前估计好的启发f
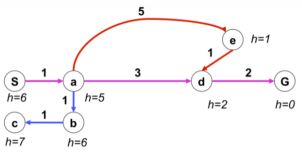
以这个图将A_ 算法运行的步骤进行一个示例:
1、首先初始化队列,将起始节点放入优先级队列中

2、弹出起始节点
可扩展的节点仅有a节点,计算f(a)=g(a)+h(a)=1+5=6
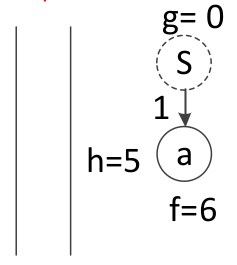
3、将扩展的节点放入优先级队列
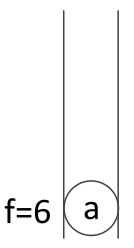
4、弹出f最小节点,扩展周围节点
弹出a节点,a节点周围可以扩展的节点为 b\d\e 。并且根据g与h值计算f值

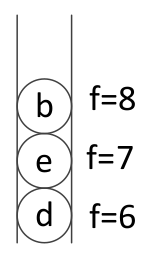
5、根据f值大小,压入队列中
d节点的f(d)=6最小,它在最下方。
点击移动机器人运动规划 | 基于图搜索的Dijkstra 和 A*算法详解 - 古月居可查看全文
![【PyTorch][chapter 25][李宏毅深度学习][Transfer Learning-1]](https://img-blog.csdnimg.cn/direct/d5d899d446d8499a83839a2eef7611e9.png)








![[Mac]安装App后“XX已损坏,无法打开“](https://img-blog.csdnimg.cn/direct/1c853bec01454fe48d87bbfa5f35f91e.png)