一种保护隐私的混合联邦学习方法

摘要

联邦学习促进了模型的协作培训，而无需共享原始数据。然而，最近的攻击表明，仅仅在培训过程中维护数据位置并不能提供足够的隐私保证。相反，我们需要一个联邦学习系统，该系统能够防止对训练期间交换的消息和最终训练的模型进行推理，同时确保生成的模型也具有可接受的预测准确性。现有的联合学习方法要么使用易受推断影响的安全多方计算（SMC），要么使用差异隐私，这可能会导致准确性较低，因为大量参与方的数据量相对较小。在本文中，我们提出了一种替代方法，利用差异隐私和SMC来平衡这些权衡。将差异隐私与安全多方计算相结合，使我们能够在保持预定义的信任率的同时，在不牺牲隐私的情况下，随着参与方数量的增加，减少噪声注入的增长。因此，我们的系统是一种可扩展的方法，可以防止推理威胁，并生成高精度的模型。此外，我们的系统可以用来训练各种机器学习模型，我们在3种不同的机器学习算法上的实验结果验证了这一点。我们的实验表明，我们的方法比最先进的解决方案更有效。

1 引入

在传统的机器学习（ML）环境中，培训数据由执行学习算法的一个组织集中保存。分布式学习系统通过使用一组学习节点访问共享数据或将数据从中心节点发送到参与节点来扩展这种方法，所有这些节点都是完全可信的。例如，Apache Spark的MLlib假设有一个可信的中心节点来协调分布式学习过程[28]。另一种方法是参数服务器[26]，它同样需要一个完全可信的中心节点来收集和聚合在不同数据集上学习的许多节点的参数。

然而，一些学习场景必须解决不太开放的信任边界，特别是当涉及多个组织时。虽然较大的数据集可以提高经过培训的模型的性能，但由于法律限制或参与者之间的竞争，组织通常无法共享数据。例如，考虑三个不同的业主为同一个城市服务的医院。与每家医院创建自己的预测模型来预测患者的癌症风险不同，医院希望创建一个在整个患者群体中学习的模型。然而，隐私法禁止他们共享患者的数据。类似地，服务提供商可以在欧洲和美国收集使用数据。由于法律限制，服务提供商的数据不能存储在一个中心位置。但是，在创建预测服务使用情况的预测模型时，应使用所有数据集。

联邦学习(FL)领域解决了这些限制性更强的环境，其中数据持有者在整个学习过程中相互协作，而不是依赖可信的第三方来保存数据[6,39]。FL中的数据持有者在本地运行机器学习算法，只交换模型参数，这些参数由一个或多个中心实体聚合和重新分配。然而，这种方法不足以提供合理的数据隐私保障。我们还必须考虑到，信息可以从学习过程[30]中推断出来，信息可以在最终训练的模型[40]中追溯到其来源。

以前的一些工作已经提出使用可信聚合器来控制隐私暴露[1]，[32]。使用局部差异隐私的FL方案也解决了隐私问题[39]，但会给来自每个节点的模型参数数据添加太多的噪声，通常会导致生成的模型性能不佳。

我们提出了一种新的联邦学习系统，它提供正式的隐私保证，考虑各种信任场景，并且与现有的隐私保护方法相比，生成的模型具有更高的准确性。数据永远不会离开参与者，使用安全多方计算（SMC）和差异隐私来保证隐私。我们通过一个可定制的信任阈值，考虑了个人参与者的潜在推断以及参与者之间的共谋风险。我们的贡献如下：

• 我们提出并实现了一个FL系统，该系统提供正式的隐私保证和模型，与现有方法相比具有更高的准确性。
• 我们包括了一个可调的信任参数，该参数考虑了各种信任场景，同时保持了改进的准确性和正式的隐私保证。
• 通过使用三种显著不同的ML模型（决策树、卷积神经网络和线性支持向量机）对我们的系统进行实验评估，我们证明了使用所提出的方法训练各种ML模型是可能的。
• 我们包括第一个联邦方法，用于私有和准确地训练神经网络模型。

本文的其余部分组织如下。我们概述了系统中的构建块。然后，我们讨论FL系统中的各种隐私注意事项，然后概述我们的威胁模型和一般系统。然后，我们提供了系统实现过程的实验评估和讨论。最后，我们给出了相关工作的概述和一些结论。

2 预定义

在本节中，我们将介绍我们的方法的构建块，并解释各种方法如何无法保护FL中的数据隐私。

2.1差别隐私

差分隐私(DP)是一个严格的数学框架，其中，当且仅当在训练数据集中包含单个实例时，算法的输出只会发生统计上无关紧要的变化，该算法可以被描述为差异隐私。例如，考虑来自特定医院的私人医疗信息。[40]的提交人表明，只要访问经过训练的ML模型，攻击者就可以推断某人是否是医院的病人，从而侵犯了他们的隐私权。DP对单个个体的影响设置了理论上的限制，从而限制了攻击者推断此类成员的能力。DP的形式化定义为[13]:

定义1(差别隐私)。随机机制K提供(ϵ，δ)-差分隐私，如果相邻数据库D1和D2仅在一个条目上存在差异，∀S⊆Range(K)，

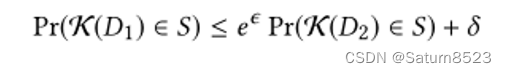
如果δ=0，则K满足ϵ-差分隐私。
为了实现DP，将噪声添加到算法的输出中。该噪声与输出的灵敏度成正比，其中灵敏度测量由于包含单个数据实例而导致的输出的最大变化。
实现DP的两种常用机制是拉普拉斯机制和高斯机制。高斯的定义是

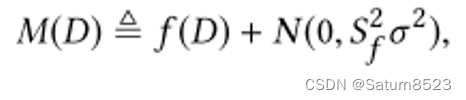
其中$N(0,S_f^2{\sigma }^2)$为均值为0，标准差为$S_f\sigma$的正态分布。将高斯机制应用于灵敏度函数Sf，如果δ≥5/4exp(−(σϵ)2/2)，且ϵ<1[16]，就能满足(ϵ，δ)-差分隐私。为了实现ϵ-差分隐私，拉普拉斯机制可以通过用从Lap（Sf/ϵ）中提取的随机变量替换$N（0，S_f^2{\sigma }^2）$[16]以相同的方式使用。当算法需要多种加性噪声机制时，隐私保证的评估遵循基本合成定理[14,15]或高级合成定理及其扩展[7,17,18,23]。

2.2 门限/阈值 同态加密

附加同态加密方案保证了以下特性：

对于某些预定义函数◦. 这种方案在隐私保护数据分析中很流行，因为不受信任的方可以对加密值执行操作。

其中一个加性同态方案是Paillier密码系统[31]，这是一个概率加密方案，基于组Z∗n2中的计算，其中n是RSA模数。在[11]中，作者对该加密方案进行了扩展，并提出了一种阈值变体。在阈值变体中，一组参与者能够共享密钥，因此小于预定义阈值的各方子集都不能解密值。

2.3联邦学习中的隐私
在集中式学习环境中，一方P使用数据集D执行一些学习算法$f$