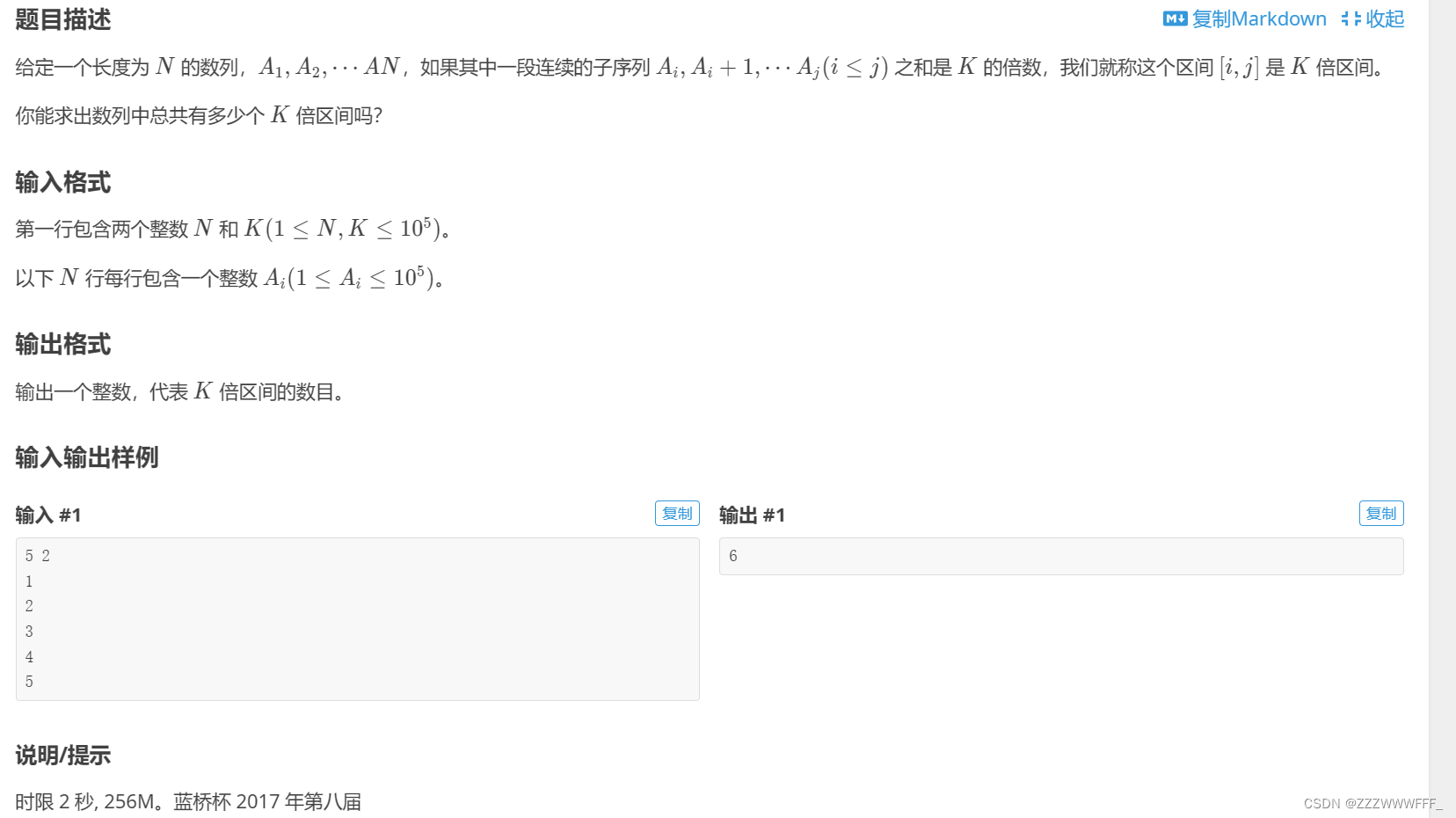
题目传送门 

思路分析：

第一思路比较容易想到，就是枚举所有的前缀和，然后遍历它们计数满足题意的前缀和数量，最后输出即可，但是这里的数列最多达到了100000，在2层循环下，总的枚举次数就达到了O(10^10)级，超时无疑

#include<iostream>
#include<vector>
#define int long long

using namespace std;

signed main()
{
	vector<int>sum;
	int n, k, value,temp=0,ans=0;
	cin >> n >> k;
	for (int i = 0; i < n; i++) {
		cin >> value;
		temp += value;
		sum.push_back(temp);//[0,i]的前缀和temp
		if (temp % k == 0) {
			ans++;
		}
		for (int j = 0; j < i; j++) {
			if ((temp - sum[j]) % k == 0) {//其他前缀和
				ans++;//通过减去下标i之前的前缀和来达到枚举其他前缀和的目的
			}
		}
	}

	cout << ans << endl;

	return 0;
}

 数论优化（来自这篇博客）：

我们假设有一个序列为：5 2 4 7 3 1 6（且k=3），则其前缀和数组的增量对k取余的结果如下所示：

a[ i ]表示该序列中的第 i 个数，S[ i ]表示该序列的前缀和增量对 k 取余的值（初始化S[0]=0）

 

不难看出，S[i]的取值在[0,k-1]之间，现在的问题是：这个值到底有什么用呢？
答案：S[i]出现的次数说明了截至当前i，前面的k倍区间的数量
比如在i=2时，当前S[i]=1，这是数字1的第一次出现，任何数字的第一次出现都不能说明前面的k倍区间数量。

但是当之后再次出现了数字1时（比如上表中i=6处），则表明现在的这个位置与前面出现数字1的位置之间构成了一个k倍区间（不包括前一个位置的那个值）。比如区间[3,6]（sum[3,6]=4+7+3+1=15，15%3=0）是一个k倍区间

继续看，在i=7时，S[i]=1又一次出现了，则表明在这个位置与其前面所有出现数字1的位置之间又能构成新的k倍区间（不包括前一个位置的那个值），比如区间[3,7]（sum[3,7]=4+7+3+1+6=21，21%3=0）是一个k倍区间；同时，也有区间[7,7]（sum[7,7]=6，6%3=0）是一个k倍区间
……

假设之后在某处i，又一次出现了数字1，那么该处又能与前面出现数字1的位置构成新的k倍区间。如果设在该处是数字1出现的第n次，那么此时能够构成的k倍区间就有n-1个，而总的k倍区间个数（包括前面所有的）则为：1+2+……+(n-1)

此时有同学就会提问了：如果是数字0第一次出现（假设为位置i），那么此时的区间[1,i]不也是一个k倍区间么？
这个提问是正确的，比如对于上面的序列，按照之前的思路，我们的流程如下：
当i=4时数字0第1次出现，但是不能说明前面的k倍区间的数量；接着当i=5时数字0第2次出现，则表明此时区间[5,5]（um[5,5]=3，3%3=0）是一个k倍区间
……
就这样直到最后
而实际上，我们一开始就忽略了区间[1,4]（sum[1,4]=5+2+4+7=18，18%3=0）也是一个k倍区间，这样的忽略导致之后每出现一次数字0，就忽略一次。比如当第2次出现数字0时，我们又忽略了区间[1,5]（sum[1,5]=5+2+4+7+3=21，21%3=0）也是一个k倍区间……
那么解决这个问题的办法也很简单，就是最后再单独加上一次所有的数字0出现的次数就行了
 

#include<iostream>
#define MAX 100010
using namespace std;

int S[MAX];//S[ i ]表示该序列的前缀和增量对 k 取余的值（初始化S[0]=0）
int b[MAX];//记录S数组中每一个数字出现次数

int main()
{
	int N, K;
	int t, i;
	cin >> N >> K;
	long long sum = 0;

	for (i = 1; i <= N; i++)
	{
		cin >> t;
		S[i] = (t + S[i - 1]) % K;
		sum += b[S[i]]++;//如果出现第二次就会加上1，出现第三次就会加上2，以此类推

	}
	cout << sum + b[0] << endl;
	return 0;
}