对称二叉树

难度：简单

给你一个二叉树的根节点 root ，检查它是否轴对称。

示例 1：

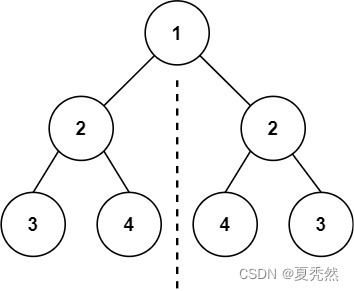
请添加图片描述

输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

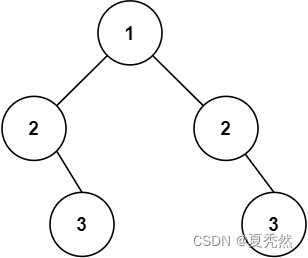
请添加图片描述

输入：root = [1,2,2,null,3,null,3]
输出：false

解法一、递归

思路：

如果一个树的左子树与右子树镜像对称，那么这个树是对称的。

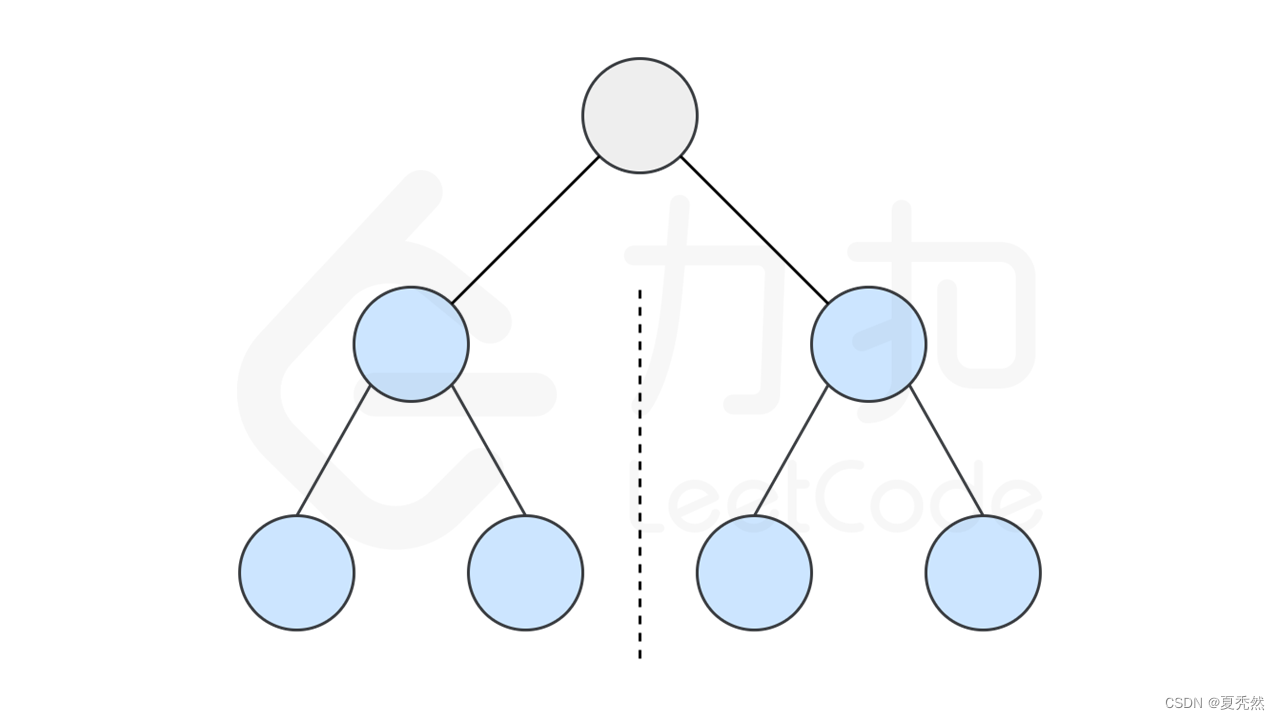
请添加图片描述

因此，该问题可以转化为：两个树在什么情况下互为镜像？

如果同时满足下面的条件，两个树互为镜像：

它们的两个根结点具有相同的值
每个树的右子树都与另一个树的左子树镜像对称

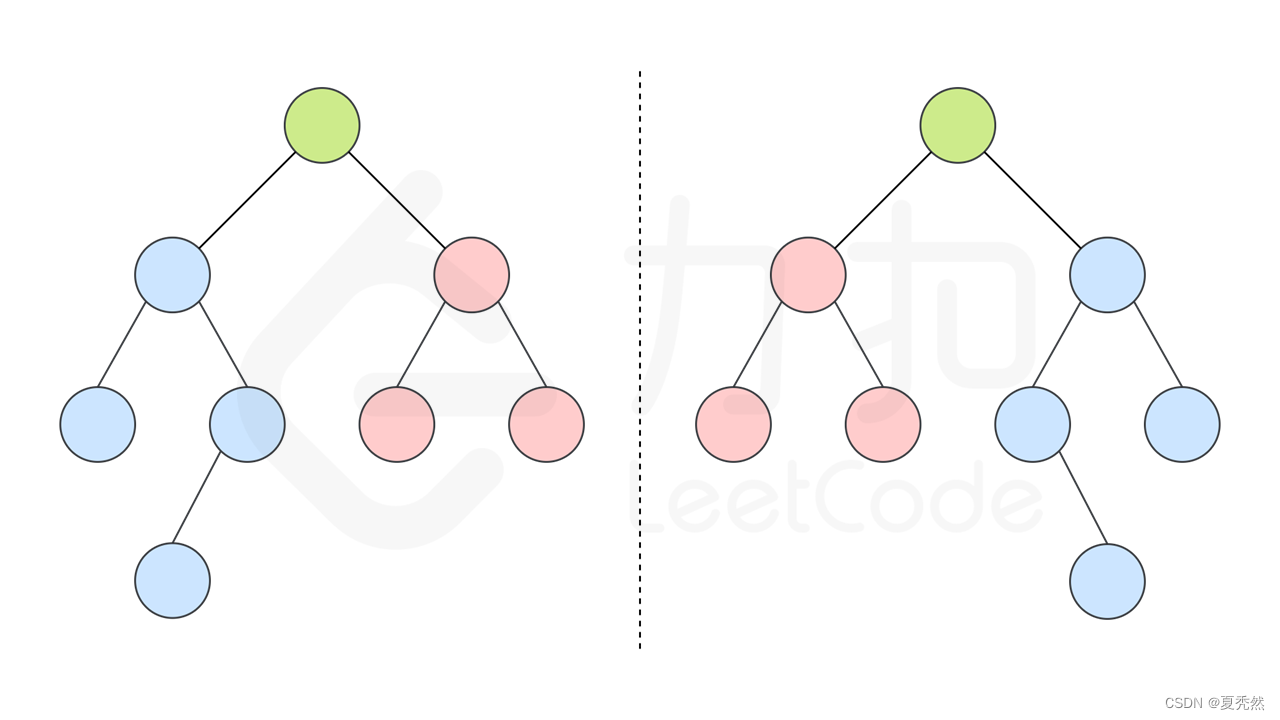
请添加图片描述

我们可以实现这样一个递归函数，通过「同步移动」两个指针的方法来遍历这棵树， $p$ 指针和 $q$ 指针一开始都指向这棵树的根，随后 $p$ 右移时， $q$ 左移， $p$ 左移时， $q$ 右移。每次检查当前 $p$ 和 $q$ 节点的值是否相等，如果相等再判断左右子树是否对称。

复杂度分析：

假设树上一共 $n$ 个节点。

时间复杂度： 这里遍历了这棵树，渐进时间复杂度为 $O (n)$ 。
空间复杂度： 这里的空间复杂度和递归使用的栈空间有关，这里递归层数不超过 $n$ ，故渐进空间复杂度为 $O (n)$ 。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isSymmetric(self, root: Optional[TreeNode]) -> bool:
        def recursion(p, q):
            if p is None and q is None:
                return True
            if p is None or q is None:
                return False
            if p.val != q.val:
                return False
            return  recursion(p.left, q.right) & recursion(p.right, q.left)
        return recursion(root.left, root.right)

解法一、迭代

思路：

首先需要引入一个队列，这是把递归程序改写成迭代程序的常用方法。初始化时我们把根节点入队两次。每次提取两个结点并比较它们的值（队列中每两个连续的结点应该是相等的，而且它们的子树互为镜像），然后将两个结点的左右子结点按相反的顺序插入队列中。当队列为空时，或者我们检测到树不对称（即从队列中取出两个不相等的连续结点）时，该算法结束。

复杂度分析：

时间复杂度： $O (n)$ 。
空间复杂度： 这里需要用一个队列来维护节点，每个节点最多进队一次，出队一次，队列中最多不会超过 $n$ 个点，故渐进空间复杂度为 $O (n)$ 。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isSymmetric(self, root: Optional[TreeNode]) -> bool:
        queue = [root.left, root.right]
        while queue:
            l, r = queue.pop(0), queue.pop(0)
            if l is None and r is None:
                continue
            if l and r and l.val == r.val:
                queue += [l.left, r.right, l.right, r.left]
            else:
                return False
        return True