链表题目总结 -- 双指针技巧

文章目录

- - 一. 合并两个有序链表
  - - 1. 思路简述
    - 2. 代码
    - 3. 总结
  - 二. 分隔链表
  - - 1. 思路简述
    - 2. 代码
    - 3. 总结
  - 三. 合并K个升序链表
  - - 1. 思路简述
    - 2. 代码
    - 3. 总结
  - 四. 单链表的倒数第 k 个节点
  - - 1. 思路简述
    - 2. 代码
    - 3. 总结
  - 五. 链表的中间结点
  - - 1. 思路简述
    - 2. 代码
    - 3. 总结
  - 六. 环形链表（链表是否有环）
  - - 1. 思路简述
    - 2. 代码
    - 3. 总结
  - 七. 环形链表 II（如何计算环的起点）
  - - 1. 思路简述
    - 2. 代码
    - 3. 总结
  - 八. 相交链表（求两个链表相交的起始点）
  - - 1. 思路简述
    - 2. 代码
    - - I. 法一
      - II. 法二
      - III. 法三
      - IV. 法四
    - 3. 总结

一. 合并两个有序链表

题目链接：
https://leetcode.cn/problems/merge-two-sorted-lists/

1. 思路简述

整一个虚拟头指针（构造一个新链表）
两个给出的链表一个节点一个节点的向后比较，val小的那个挂在新链表上（像是一个简单选择排序）
如果一个链表比另一个链表长，把多余的那个部分直接挂在新链表后面（因为题目给的是两个有序链表）。

2. 代码

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
        ListNode p = new ListNode();
        ListNode p1 = p;

        while(list1 != null && list2 != null){
            if(list1.val > list2.val){
                p1.next = list2;
                list2 = list2.next;
            }
            else{
                p1.next = list1;
                list1 = list1.next;
            }
            p1 = p1.next;
        }
        if(list1 != null){
            p1.next = list1;
            //这句，完全不需要写，只要list1没完直接整体挂在后面就行了
            //p1 = p1.next;
        }
        if(list2 != null){
            p1.next = list2;
            //这句和上面一样，也不用写
            //p1 = p1.next;
        }
        return p.next;

    }
}

3. 总结

设立p节点，是为了简化边界判断的操作。
一般的题目，都是没有头结点的，所以最后返回的是p.next。
ListNode p = new ListNode();申请空间的意义，是由于它必须存在next指针，否则没法往后面挂。
两个给定的链表不需要再申请额外的工作指针，因为比一次，对应的节点就已经挂在新链表上了，不需要考虑回溯的问题。
虽然说这代码看起来很烂，有很多冗余的部分，但可读性强啊，也有利于去编写。
时间复杂度：O(len(A) + len(B))
空间复杂度：O(1)

二. 分隔链表

题目链接：
https://leetcode.cn/problems/partition-list//

1. 思路简述

建立两个子链表，比x值小的节点挂一个链表上，另一些节点挂在另外一个链表上。
保存挂在链表上节点的后继节点，同时将该节点的next清空，保证那条子链是一个独立的链。
最后将两个链表拼接在一起。

2. 代码

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode partition(ListNode head, int x) {
    //建立两个虚拟的头结点，用于引导两个子链表
        ListNode list1 = new ListNode();
        ListNode list2 = new ListNode();
    //p1,p2分别为两个子链表上的工作指针    
        ListNode p1 = list1, p2 = list2;
    //p为初始链表的工作指针
        ListNode p = head;
    //temp为初始链表的临时指针，用于保存挂在list1或list2上节点的后继节点，使原链表中每一个节点都能访问到
        ListNode temp = null;

        while(p != null){
            if(p.val < x){
                p1.next = p;
                p1 = p;
            }
            else{
                p2.next = p;
                p2 = p;
            }
            temp = p.next;
            p.next = null;
            p = temp;
        }
    //将list2挂在list1上，由于链表默认是没有虚拟节点的，所以使用p1.next来接收值
        p1.next = list2.next;
    //同理，list1为虚拟头结点，返回list1.next
        return list1.next;
    }
}

3. 总结

这道题其实不是很难，但是由于引入了很多指针，所以显得很绕，博主第一次做这个题，就把自己绕进去了，卡在了temp指针哪一步，不知道怎么才能保证所有节点都能访问到。

凡是需要申请空间的变量，最好就不要动了，引入新的变量来充当工作指针，要不然很乱很乱。
这道题和上道题很像，都是需要比较。第一个题为1 -> 2；这个题而是：1 -> 2 -> 1。
最难的就是temp那一块，需要双指针暂存后继节点，同时清空子链表的末尾（最后节点的.next = null）。
时间复杂度：O(n)
空间复杂度：O(1)

三. 合并K个升序链表

题目链接：https://leetcode.cn/problems/merge-k-sorted-lists/

1. 思路简述

处理边界情况。
建立优先队列，将所有链表的头节点放入队列，形成一个小根堆。
不断的筛选出最小的节点，挂在新的链表node上。

2. 代码

import java.util.*;

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
    //判断极端情况
        if(lists.length == 0)
            return null;
    //建立虚拟头节点
        ListNode node = new ListNode();
        ListNode p = node;
    //创建优先级队列
        PriorityQueue<ListNode> pq = new PriorityQueue<>(lists.length,new Comparator<ListNode>(){
             public int compare(ListNode a, ListNode b){
                return a.val - b.val;
            }
        });
   /* 
        法二：也可以这么创建优先队列
        PriorityQueue<ListNode> pq = new PriorityQueue<>(
        lists.length, (a, b)->(a.val - b.val));
   */
   
    /*
		把所有链表的头结点放入优先队列中，形成一个小根堆。因为各个子列表是升序的，
		所以不用担心，中间会有比它更小的值。
    */

        for(ListNode node1 : lists){
            if(node1 != null)
                pq.add(node1);
        }
	/*
		不断筛选最小值输出。以第一个为例：如果头结点被筛选走了，就第二个节点加入小根堆。
		因为每个子链表都是升序的，所以保证了，每次进入小根堆的其实都是当前链表当中的最小值。
		一直筛选，直到所有的链表当中的节点都搞完，结束。
	*/
        while(!pq.isEmpty()){
            ListNode min = pq.poll();
            p.next = min;
            p = min;
            if(p.next != null)
                pq.add(p.next);

        }

        return node.next;
    }
}

3. 总结

时间复杂度：O(Nlog(k)) （k为链表的个数，N为结点的总个数，找到最小结点O(1)，调整堆顺序O(logk)）
空间复杂度：O(n)（创建一个新的链表开销为O(n)；优先队列的开销为O(k)，远比大多数情况的n要小）
为什么创建好一个数组，默认就有length属性呢？
- 因为数组创建的时候，需要分配空间，长度是一个定值（类型为：public final int ），所以只要数组创建好了，就可以使用.length属性。
- 具体的.length和.length()两种方法对比，请看下面这篇博客：
- https://blog.csdn.net/qq_39671159/article/details/128584905
遇见下面两种情况，直接记住：数组名.length == 0为条件（eg：lists.length == 0）
- 如果使用lists[0] == null，会直接报错（空指针异常）

输入：lists = [ ]
输出：[ ]

输入：lists = [[ ]]
输出：[ ]

PriorityQueue创建中，会使用二叉堆对自身进行排序。想要知道它内部是怎么实现的，请参考https://labuladong.github.io/algo/di-yi-zhan-da78c/shou-ba-sh-daeca/er-cha-dui-1a386/和算法4这本书中优先队列这一小节。
创建优先队列的时候，为什么对比的方法是前大于后，也就是说，为什么这样创建出来的是小根堆？？？
- 算法4里面关于这个问题，有一句话很有意思：MaxPQ（基于大根堆的优先队列）的任意实现都能很容易地转化为MinPQ（基于小根堆的优先队列）的实现，反之亦然，只需要改变一下less()比较的方向即可。
- 我们再去研究一下swim()方法
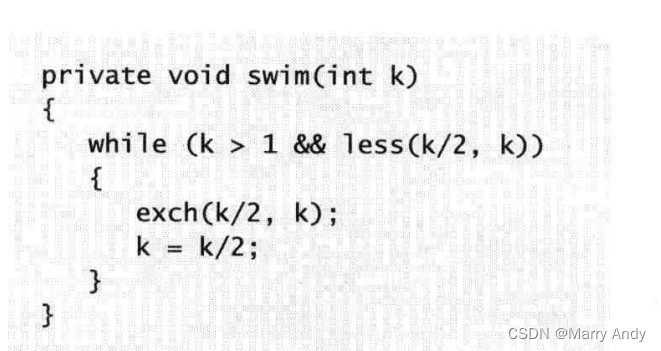
- 上面两个图说的是基于大根堆的优先队列，K/2就是父节点，K则是子节点。我们带入less()方法，父节点的值如果比子节点的值小，那我们交换父子节点（也就是说父节点的值一定要大于子节点的值），这明显是一个大根堆的有序化过程。同理，看本题当中重写的compare方法（return a.val - b.val;），显然是一个小根堆的有序化的比较方法。
本质上还是一个排序的问题，前面两个题都是两个链表进行排序，而这个题则是多个链表进行排序，以后可以直接联想到优先队列，使用二叉堆来处理问题。

四. 单链表的倒数第 k 个节点

题目链接：https://leetcode.cn/problems/remove-nth-node-from-end-of-list/

1. 思路简述

先找到倒数 k + 1个节点，因为我们要知道它的前一个是谁，才能将删除后的链表连在一起。
倒数第k + 1个节点，不就相当于，这个节点到链尾的距离是k + 1吗，那我们，让p1 = head，过k+1个距离后，设置p2 = head；（使两个指针中间的距离刚好使k + 1）
两个指针一直向前同步移动，知道p1 = null；p2则是我们要删除的节点。

2. 代码

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode findFromEnd(ListNode head, int n){
        ListNode p1 = head;
        while(n != 0){
            p1 = p1.next;
            n--;
        }
        ListNode p2 = head;
        while(p1 != null){
            p2 = p2.next;
            p1 = p1.next;
        }
        return p2;
    }
    public ListNode removeNthFromEnd(ListNode head, int n) {
        ListNode list = new ListNode(-1);
        //引入头结点，完全是为了，让头结点和其他结点一样，便于处理
        list.next = head;
		//如果我们单单是为了就出倒数第K个节点，就没有引入头结点的必要，因为根本涉及不到对头结点的操作
		//这里一定是 list而不是 head，考虑边界情况（[1]，1 ）这种情况，如果找倒数n + 1的结点，会出现空指针异常
        ListNode x = findFromEnd(list, n + 1);
        x.next = x.next.next;

        return list.next;
    }
}

3. 总结

这个题非常的巧妙，将本来看似逆向的问题（求逆向第k个），转换成了正向问题，用双指针同步移动（k个距离，直到快指针为null）解决了问题。
注意边界问题，很容易出现空指针异常。
常常具备构造虚拟头结点的思想，会简便很多。
这道题虽然也是双指针，但是和上面的几个题不同，不再是排序的问题。
时间复杂度：O(n)
空间复杂度：O(1)

五. 链表的中间结点

题目链接：https://leetcode.cn/problems/middle-of-the-linked-list/

1. 思路简述

设两个指针，一个一次跑一格子，一个一次跑两格子。
让两个指针一起向后跑，快指针跑到末尾，慢指针指的就是

2. 代码

带头结点

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode middleNode(ListNode head) {
        ListNode list = new ListNode(-1);
        list.next = head;
        ListNode p1 = list;
        ListNode p2 = p1;
	/*
		下面这个while循环完全可以改成：
		while(p2 != null && p2.next != null){
            p1 = p1.next;
            p2 = p2.next.next;
        }
	*/
        while(p2 != null){
            if(p2.next == null)
                break;
            p1 = p1.next;
            p2 = p2.next.next;
        }
        if(p2 == null)
            return p1;
        else 
            return p1.next;
    }
}

不带头结点

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode middleNode(ListNode head) {
        ListNode p1 = head;
        ListNode p2 = p1;

        while(p2 != null && p2.next != null){
            p1 = p1.next;
            p2 = p2.next.next;
        }

        return p1;
    }
}

3. 总结

快慢指针的问题，巧妙的将求解中间结点的问题转换成了：求两个指针中间距离的问题，和上一题有异曲同工之妙。
有一点落入了设置头结点的固定陷阱中，面试的时候，还是先考虑没有虚拟头结点的情况，如果不好算，那么再加虚拟头结点。笔试就无所谓。
写上面while循环的时候，我一直再想或，或，或的问题，一直报空指针，所以才改成那个样子，以后，或想不出来，可以想想与运算。
时间复杂度：O(n)
空间复杂度：O(1)

六. 环形链表（链表是否有环）

题目链接：https://leetcode.cn/problems/linked-list-cycle/

1. 思路简述

其实这问题和上题（链表的中间结点）的求法大致相似，只要稍稍改一下就可以。
快慢指针同时从head往后面跑，上道题是快指针跑到链的末尾就停止，而这道题是一直跑，如果有环，那么快慢指针一定相遇；如果没环，一定能出这个循环。

2. 代码

public boolean hasCycle(ListNode head){
	ListNode p1 = head;
	ListNode p2 = p1;
	
	while(p2 != null && p2.next != null){
	//其实还是上面题的那个循环，如果它能从这个循环中走出来，那么它一定没环；如果有环，快慢指针肯定会相遇，且快指针比慢指针多走了一圈
		p1 = p1.next;
		p2 = p2.next.next;
	
		if(p1 == p2)
			return true;
	}
	return false;
	
}

如果有环，快慢指针肯定会相遇，且快指针比慢指针多走了一圈（慢指针 slow 走了 k 步，那么快指针 fast 一定走了 2k 步），盗一张东哥的图：
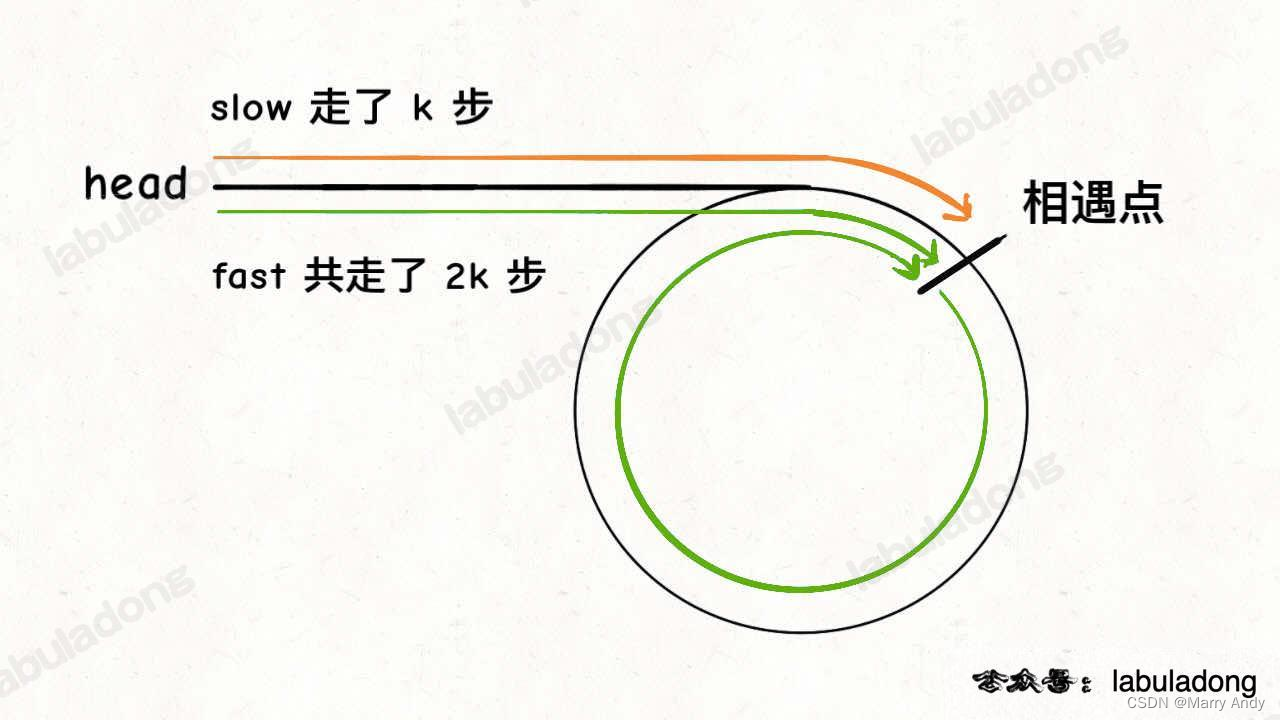
在这里插入图片描述
实在不理解就用笔画一画，用2个结点的环链表和3个结点的环链表做实验就可以。

3. 总结

上道题是快指针跑到链的末尾就停止，而这道题是一直跑，如果有环，那么快慢指针一定相遇；如果没环，一定能出这个循环。
时间复杂度：O(n)（n为链表长度，不存在环时，遍历一遍链表就结束；使用相对速度来理解，快指针的相对速度为1，慢指针原地不动，那么也就是考虑快指针前往相遇点要花的时间，相遇点最靠后，也就在这个链表环起点的前一个结点，不会超过n）
空间复杂度O(1)

七. 环形链表 II（如何计算环的起点）

题目链接：https://leetcode.cn/problems/linked-list-cycle-ii/

1. 思路简述

设置快慢指针，让它们第一次相遇。
相遇之后将快指针（或者慢指针）放到起点，然后同步移动，再一次相遇的地点，就是环的起点。

这道题和上道题也差不多，在上道题的基础上做了一点点改动，下面解释一下具体的细节：

首先，分析题意，判断环的起点，那么这个链表就一定存在环，那么就要解决有环的问题，也就是上个题所处理的问题。
盗一张东哥的图，嘿嘿嘿。假设快慢指针在图中的相遇点相遇，我们知道：慢指针 slow 走了 x 步，那么快指针 fast 一定走了 2x步。那么，慢指针跑到了相遇点，快指针就一定多走了一倍的路程。相当于：慢指针在相遇点没动，快指针从相遇点，走了慢指针从head到相遇点这么长的路程。他们最终又相遇了，就是说快指针从相遇点又走到了相遇点（一直在转圈圈），那么快指针走的路程一定是环的长度的整数倍。
假设快慢指针已经在相遇点相遇，现在把慢（快）指针放到开始位置（slow == head; or fast == head;），另一个指针不动，开始同步向前。
解释一下为什么第二次要同步向前？
- 根据上面的分析，我们知道：慢指针从head到相遇点这么长的路程，相当于快指针从相遇点到相遇点跑的路程，就是在转圈圈。如果是按照原来的方法（快指针走的路是慢指针走的路的2倍），那么他们最终还是会在相遇点相遇，而不是一定是环起点（环起点和相遇点有可能不重合）。
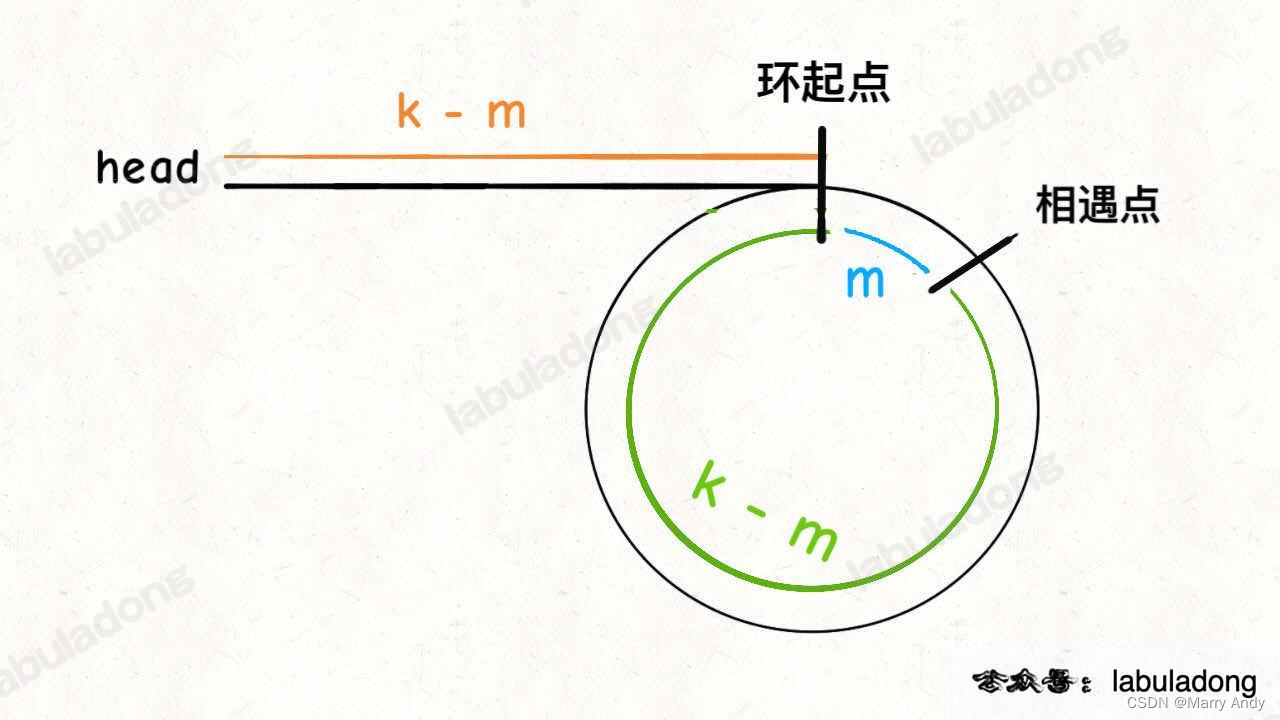
- 假设环的长度是k，假设快指针走的路程一定是环的长度的1倍，相遇点离环起点的有m的距离。
- 若是同步向前，大家看图，当快慢指针同时走k - m的距离之后，它们会在环起点相遇。

2. 代码

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode p1 = head;
        ListNode p2 = p1;

        while(p2 != null && p2.next != null){
            p1 = p1.next;
            p2 = p2.next.next;
            
            if(p1 == p2)
                break;
        }

        if(p2 == null || p2.next == null)
            return null;

        p1 = head;
        while(p1 != p2){
        //一定是同步移动
            p1 = p1.next;
            p2 = p2.next;
        }
        return p1;
    }
}

3. 总结

博主自己做的时候，画了画图，认为环起点和相遇点一定是同一个点，最后发现不是这个样子的。当把慢指针放到head处后，又天真的认为按原来的快慢指针方法（速度不同）一定行，结果g了。
代码量虽然不大，思维要求还是很高的，尤其是这一点：快指针走的路程一定是环的长度的整数倍。想了很久。
时间复杂度：O(N)，其中 N 为链表中节点的数目。在最初判断快慢指针是否相遇时，慢指针走过的距离不会超过链表的总长度；随后寻找入环点时，走过的距离也不会超过链表的总长度。因此，总的执行时间为 O(N)+O(N)=O(N)
空间复杂度：O(1)。我们只使用了p1，p1两个指针。

八. 相交链表（求两个链表相交的起始点）

题目链接：https://leetcode.cn/problems/intersection-of-two-linked-lists/

1. 思路简述

求两个链表相交的起始点，首先要考虑的是两个链表是否相交的问题。如果我们能保证两个链表同时到达相交的区域，就能进行判断了。
在这里插入图片描述
法一：

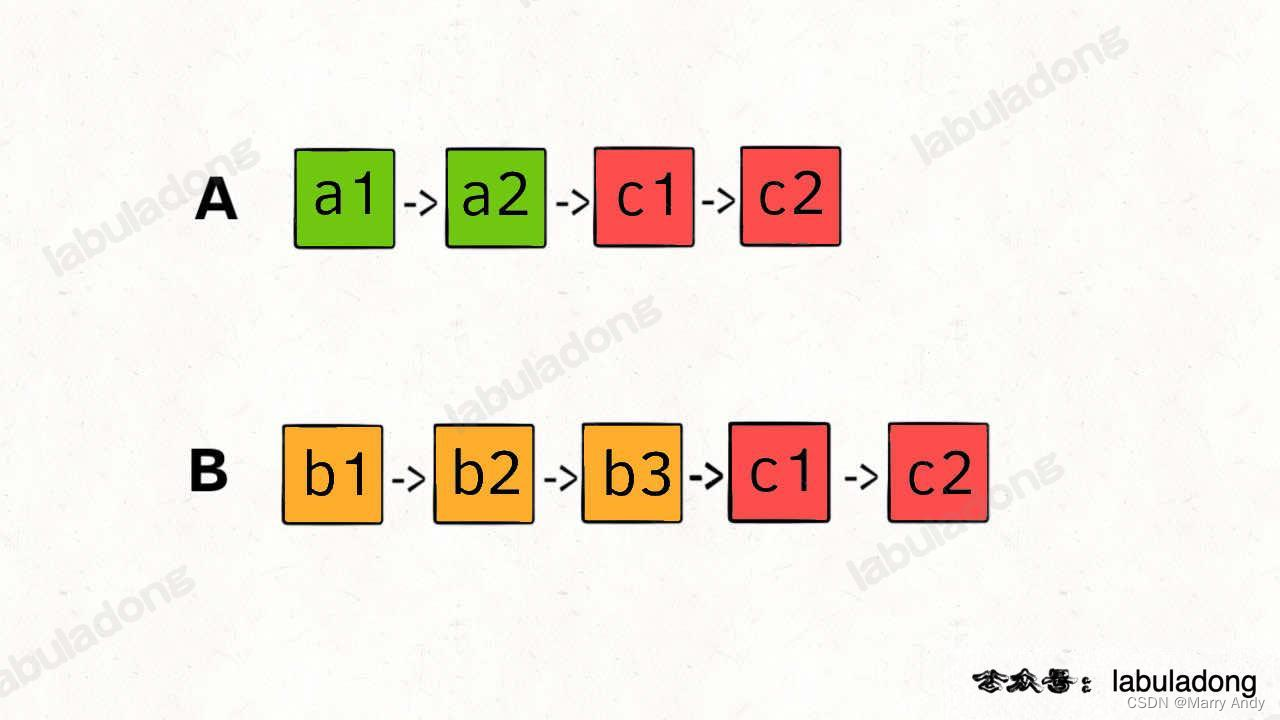
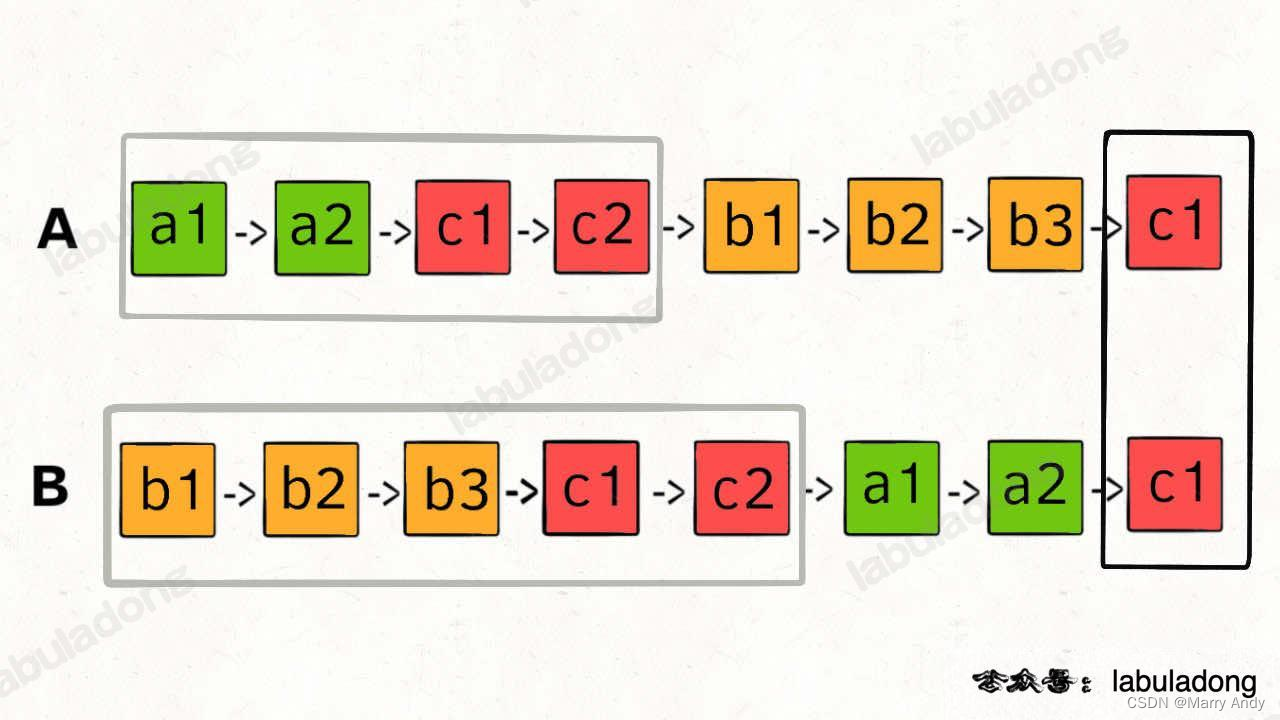
将链表A和链表B连接起来。（一边遍历，一边连接，不存在专门的连接步骤）
- 将A，B链表连接起来，形成新链表p1；将B，A链表连接起来，形成新链表p2。
- 这样不管A，B谁长，最终合起来的链表（p1和p2）长度是一致的，那么也就可以同时到达相交区域，如下图所示。
如果相交，输出的是相交结点；不相交，输出的是null。

2. 代码

I. 法一

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        ListNode p1 = headA;
        ListNode p2 = headB;

        while(p1 != p2){
            if(p1 == null)
     		//A完了接B
                p1 = headB;
            else
                p1 = p1.next;
                
            if(p2 == null)
           	//B完了接A
                p2 = headA;
            else
                p2 = p2.next;
        }
        return p1;
    }
}

II. 法二

用了两个变量lenA，lenB来存储A，B表的长度。
让相对长的链表先走，直到两个链表剩余的长度相同，再开始同时遍历、比较。
如果相交，输出的是相交结点；不相交，输出的是null。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        ListNode p1 = headA;
        ListNode p2 = headB;
        int lenA = 0;
        int lenB = 0;

        while(p1 != null){
            lenA++;
            p1 = p1.next;
        }
        while(p2 != null){
            lenB++;
            p2 = p2.next;
        }

        p1 = headA;
        p2 = headB;

        if(lenA > lenB)
            for(int i = 0; i < lenA - lenB; i++)
                p1 = p1.next;
        else
            for(int i = 0; i < lenB - lenA; i++)
                p2 = p2.next;

        while(p1 != p2){
            p1 = p1.next;
            p2 = p2.next;
        }
        return p1;
    }
}

III. 法三

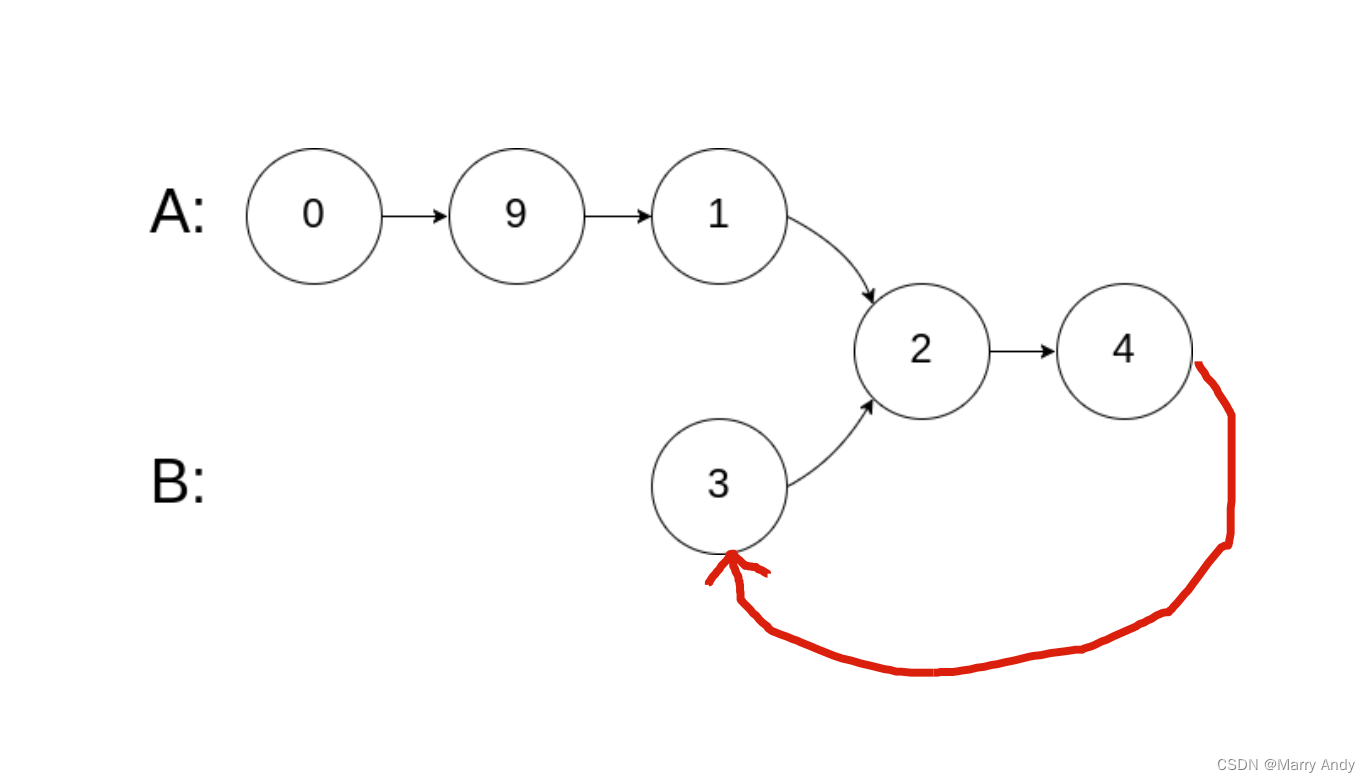
将A的末尾和B连接起来，将问题转换成求链表的成环起始点问题（也就是问题七）。
一定要注意，题目中强调要不能改变链表的结构，那么在输出之前一定记得变回来，本题使用的是temp指针来处理。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
        public ListNode detectCycle(ListNode head) {
        ListNode p1 = head;
        ListNode p2 = p1;

        while(p2 != null && p2.next != null){
            p1 = p1.next;
            p2 = p2.next.next;
            
            if(p1 == p2)
                break;
        }

        if(p2 == null || p2.next == null)
            return null;

        p1 = head;
        while(p1 != p2){
        //一定是同步移动
            p1 = p1.next;
            p2 = p2.next;
        }
        return p1;
    }
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        ListNode p1 = headA;
        ListNode p2 = headB;
        //临时指针，处理链表结构改动问题
        ListNode temp = null;
        while(p1.next != null)
            p1 = p1.next;
        p1.next = headB;
        
        temp = p1;
        p1 = detectCycle(headA);
        //将结构改回去
        temp.next = null;
        
        return p1;
    }
}

IV. 法四

使用HashSet数据结构，往里面加链表A。之后遍历链表B，判断结点是否在里面。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        Set<ListNode> hashset = new HashSet<ListNode>();
        ListNode p = headA;

        while(p != null){
            hashset.add(p);
            p = p.next;
        }

        p = headB;
        while(p != null){
            if(hashset.contains(p))
                return p;
            p = p.next;
        }
        return null;
    }
}

3. 总结

最好的解法还是第一个解法，空间复杂度为 O(1)，时间复杂度为 O(N)。算法十分新颖。
解法二，虽然代码多一些，空间复杂度仍为 O(1)，时间复杂度仍为 O(N)。
算法三，将问题转化成了问题七，挺有意思的，空间复杂度仍为 O(1)，时间复杂度仍为 O(N)。
解法四，时间复杂度O(len(A) + len(B))，空间复杂度O(len(A))。

参考：
https://labuladong.github.io/algo/di-yi-zhan-da78c/shou-ba-sh-8f30d/shuang-zhi-0f7cc/
https://leetcode.cn/problems/intersection-of-two-linked-lists/solution/xiang-jiao-lian-biao-by-leetcode-solutio-a8jn/
https://leetcode.cn/problems/linked-list-cycle-ii/solution/huan-xing-lian-biao-ii-by-leetcode-solution/