说明

【数据结构与算法之美】专栏学习笔记。

什么是复杂度？

复杂度也叫渐进复杂度，包括时间复杂度和空间复杂度，用来分析算法执行效率与数据规模之间的增长关系，可以粗略地表示，越高阶复杂度的算法，执行效率越低。

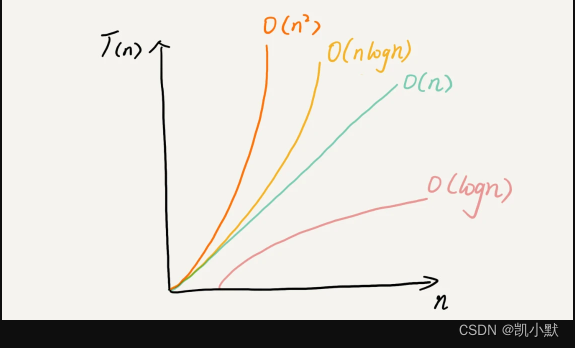
常见的复杂度从低阶到高阶有：O(1)、O(logn)、O(n)、O(nlogn)、O($n^2$ )。

为什么需要复杂度分析？

性能测试的局限性：

• 测试结果非常依赖测试环境
• 测试结果受数据规模的影响很大

复杂度分析有不依赖执行环境、成本低、效率高、易操作、指导性强的特点。

大 O 复杂度表示法

也叫作渐进时间复杂度（asymptotic time complexity），简称时间复杂度，它不具体表示代码真正的执行时间，只是表示代码执行时间随数据规模增长的变化趋势。

算法的执行效率，粗略地讲，就是算法代码执行的时间。所有代码的执行时间 T(n) 与每行代码的执行次数 f(n) 成正比。

T(n) = O(f(n))

• T(n)：表示代码执行的时间
• n：表示数据规模的大小
• f(n) ：表示每行代码执行的次数总和
• O：表示代码的执行时间 T(n) 与 f(n) 表达式成正比。

举个例子：

int cal(int n) {
	int sum = 0;
	int i = 1;
	int j = 1;
	for (; i <= n; ++i) {
		j =1;
		for (; j <= n; ++j) {
 			sum = sum +  i * j;
		}
	}
}

上面代码，我们假设每个语句的执行时间是 unit_time，那么

• 第 2、3、4 行代码都需要 1 个 unit_time 的执行时间
• 第 5、6 行代码循环执行了 n 遍，需要 2n * unit_time 的执行时间
• 第 7、8 行代码循环执行了 $n^2$ 遍，需要 2$n^2$ * unit_time 的执行时间

综上，上面整段代码总的执行时间 T(n) = (2$n^2$ + 2n + 3) * unit_time。

大 O 时间复杂度表示法：T(n) = O(2$n^2$ + 2n + 3)。当 n 很大，低阶、常量、系数不左右增长趋势，可以忽略这些项，记录一个最大量级即可：T(n) = O($n^2$)。

时间复杂度分析

1、循环执行次数最多法则

只关注循环执行次数最多的一段代码

大 O 复杂度表示方法只是表示一种变化趋势，通常会忽略掉公式中的常量、低阶、系数，只需要记录一个最大阶的量级即可。

int cal(int n) {
	int sum = 0;
	int i = 1;
	for (; i <= n; ++i) {
		sum = sum + i;
	}
	return sum;
}

比如上面这个例子，循环执行次数最多的是第 4、5 行代码，时间复杂度就是 O(n)。

2、加法法则

总的时间复杂度就等于量级最大的那段代码的时间复杂度。

int cal(int n) {
	int sum_1 = 0;
	int p = 1;
	for (; p < 100; ++p) {
		sum_1 = sum_1 + p;
	}
	
	int sum_2 = 0;
	int q = 1;
	for (; q < n; ++q) {
		sum_2 = sum_2 + q;
	}
	
	int sum_3 = 0;
	int i = 1;
	int j = 1;
	for (; i <= n; ++i) {
		j = 1; 
		for (; j <= n; ++j) {
			sum_3 = sum_3 +  i * j;
		}
	}
	
	return sum_1 + sum_2 + sum_3;
}

上面代码可以分成3段代码来看：

• 第一段：可以忽略掉
• 第二段：时间复杂度为 O(n)
• 第三段：时间复杂度为 O($n^2$)

这三段代码的时间复杂度，取其中最大的量级 O($n^2$)。

公式表示如下：

T(n) = T1(n) + T2(n) = max(O(f(n)), O(g(n))) = O(max(f(n), g(n)))

3、乘法法则

嵌套代码的复杂度等于嵌套内外代码复杂度的乘积。

公式如下：

T(n) = T1(n) * T2(n) = O(f(n)) * O(g(n)) = O(f(n) * g(n))

int cal(int n) {
	int ret = 0; 
	int i = 1;
	for (; i < n; ++i) {
		ret = ret + f(i);
	} 
} 

int f(int n) {
	int sum = 0;
	int i = 1;
	for (; i < n; ++i) {
		sum = sum + i;
	} 
	return sum;
}

上面的代码里 for 循环嵌入了另外一个函数，这个代码时间复杂度就是T(n) = T1(n) * T2(n) = O(n * n) = O($n^2$)。

几种常见时间复杂度实例分析

复杂度量级分类：

• 多项式量级
• 非多项式量级
  • O($2^n$)
  • O(n!)

时间复杂度为非多项式量级的算法问题叫作 NP（Non-Deterministic Polynomial，非确定多项式）问题。

下面看几种常见的多项式时间复杂度：

1、O(1)

O(1) 只是常量级时间复杂度的一种表示方法，并不是指只执行了一行代码。只要算法中不存在循环语句、递归语句，代码的执行时间不随 n 的增大而增长，不管代码多少行，其时间复杂度也是Ο(1)。

2、O(logn)、O(nlogn)

i=1;
while (i <= n)  {
	i = i * 2;
}

上面列出来就是这样的效果

$2^0$ $2^1$ … $2^x$ = n

这里知道 x 值即可，就能知道 while 这行代码执行的次数，我们通过 $2^x$ = n 求解得到 x = $lo{g}_2$n，时间复杂度就是 O($lo{g}_2$n)。

由于对数之间是可以互相转换的，所以在对数阶时间复杂度的表示方法里，我们可以忽略对数的“底”，统一表示为 O(logn)。

对于 O(nlogn) 就是上面讲的乘法规则：一段代码的时间复杂度是 O(logn)，循环执行 n 遍，时间复杂度就是 O(nlogn) ，比如，归并排序、快速排序的时间复杂度都是 O(nlogn)。

3、O(m+n)、O(m*n)

int cal(int m, int n) {
	int sum_1 = 0;
	int i = 1;
	for (; i < m; ++i) {
		sum_1 = sum_1 + i;
	}
	
	int sum_2 = 0;
	int j = 1;
	for (; j < n; ++j) {
		sum_2 = sum_2 + j;
	}
	
	return sum_1 + sum_2;
}

上面代码里 m 和 n 是表示两个数据规模，无法确定那个大，所以不能忽略其中一个，这里的时间复杂度就是 O(m + n)。

• 加法规则：T1(m) + T2(n) = O(f(m) + g(n))
• 乘法法则：T1(m) * T2(n) = O(f(m) * f(n))。

空间复杂度分析

也叫渐进空间复杂度（asymptotic space complexity），表示算法的存储空间与数据规模之间的增长关系。

void print(int n) {
	int i = 0;
	int[] a = new int[n];
	for (i; i <n; ++i) {
		a[i] = i * i;
	}
	
	for (i = n-1; i >= 0; --i) {
		print out a[i]
	}
}

上面代码空间复杂度就是 O(n)。

• 第 2 行代码：申请了一个空间存储变量 i，但是它是常量阶的，跟数据规模 n 没有关系，可以忽略。
• 第 3 行代码：申请了一个大小为 n 的 int 类型数组

常见的空间复杂度就是 O(1)、O(n)、O($n^2$ )，像 O(logn)、O(nlogn) 对数阶复杂度平时用不上，空间复杂度分析比时间复杂度分析要简单很多。