题目1：

给定一个大小为 n 的数组 nums ，返回其中的多数元素。多数元素是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在多数元素。
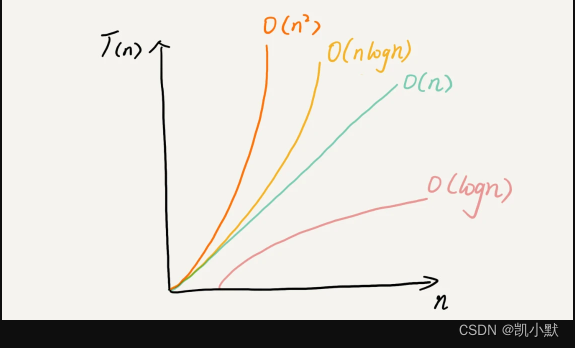
进阶：尝试设计时间复杂度为 O(n)、空间复杂度为 O(1) 的算法解决此问题。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/majority-element
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

分析：
方法1：可以一个数接着一个数进行比较，找到重复的数就计数1。当计数大于 ⌊ n/2 ⌋ 的时候直接返回值。缺点：不满足时间复杂度的要求。
方法2：一个数组中有一个数字出现次数大于 n/2 ，从第 0 个字符开始，假设它就是最多的那个数字，遇到相同的数字则计数 +1 ，遇到不同的则计数 -1 ，其实就是互相消耗，等到计数为 0 的时候，表示本次互拼完毕，从下一个字符重新开始互拼，但是归根结底出现次数大于 n/2 的这个数字数量更多，因此也是最后保留的字符。优点：只需要比较一次就可找出数据

int majorityElement(int* nums, int numsSize)
{
    //控制循环
    int i;
    //设第一个元素就是为所求
    int tmp = nums[0];
    //计数为1
    int count = 1;
    //遍历剩下的元素
    for (i = 1; i < numsSize; i++)
    {
        //如果和计数的元素相等，计数自增1,不相等就自减1
        if (nums[i] == tmp)
        {
            count++;
        }
        else
        {
            count--;
        }
        //当count为零的时候，将设的元素开始到下个元素
        if (count == 0)
        {
            tmp = nums[i + 1];
        }
    }
    //循环到最后，此时标记的元素就是所求的元素
    //因为当一个数组中，有大于⌊ n/2 ⌋ 的元素，一定存在m小于⌊ n/2 ⌋ 的整数，和m个不相同的元素相消
    //相消后剩下的元素就是所求
    return tmp;
}

题目二：

*给你一个整数数组 nums，返回数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积。

题目数据保证数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位整数范围内。

请不要使用除法，且在 O(n) 时间复杂度内完成此题。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/product-of-array-except-self
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。*/

int* productExceptSelf(int* nums, int numsSize, int* returnSize)
{
    *returnSize = numsSize;
    int* answer = (int*)calloc(numsSize, sizeof(int));
    if (answer == NULL)
    {
        printf("No space avalible\n");
        exit(1);
    }
    int left = 1;
    int right = 1;
    for (int i = 0; i < numsSize; i++)
    {
        answer[i] = left;
        left *= nums[i];
    }
    for (int i = numsSize; i >= 0; i++)
    {
        answer[i] = right;
        right *= nums[i];
    }
    return answer;
}