深入理解数据结构第三弹——二叉树（3）——二叉树的基本结构与操作

news2024/10/7 17:35:45

二叉树（1）：深入理解数据结构第一弹——二叉树（1）——堆-CSDN博客

二叉树（2）：深入理解数据结构第二弹——二叉树（2）——堆排序及其时间复杂度-CSDN博客

前言：

在前面我们讲了堆及其应用，帮助我们初步了解了二叉树的一些原理，但那与真正的二叉树仍有不同，今天我们就来正式学习一下二叉树的基本结构及其基本操作

一、什么是二叉树？

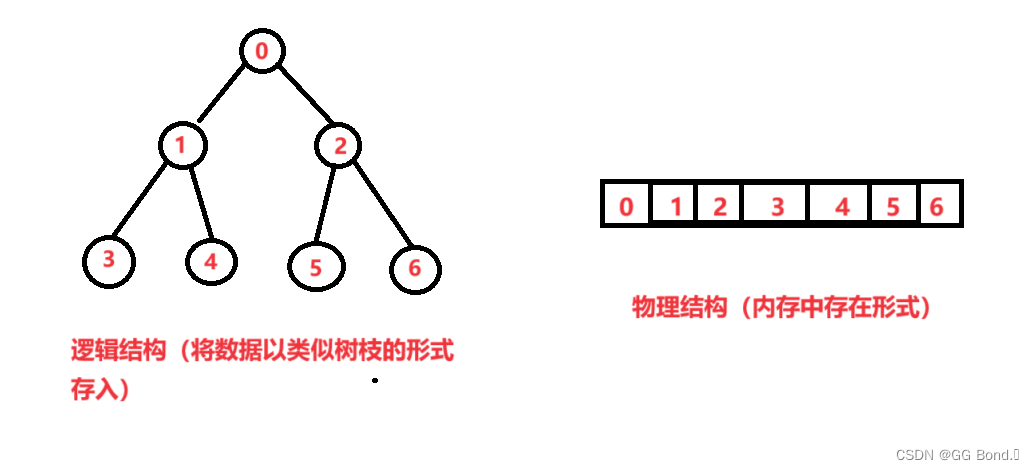
在前面的文章中我们已经提到过二叉树的结构及其特点，这里我们不过多赘述，有不理解的可以点文章开头的链接去前面看一下

二、二叉树的节点结构

二叉树有左右子树之分，且二叉树与我们所学的其他数据结构不同的点在于，之前我们所学的都是各类插入或者删除等等，但是二叉树需要做的操作是运用递归遍历，所以二叉树的节点结构与之前几个有很大不同

typedef int TreeDataType;
typedef struct Tree
{
	TreeDataType a;
	struct Tree* left;
	struct Tree* right;
}Tree;

节点结构里面定义有两个递归，是为了方便后面的遍历

三、二叉树的遍历

二叉树的遍历是我们学习二叉树首先要了解的东西，我们都知道二叉树其实就是一串数组，那我们是如何访问他们的呢？这里就牵扯到了遍历顺序的问题。

二叉树的遍历有三种形式：前序、中序和后序

  1. 前序遍历：

    • 特点：按照“根-左-右”的顺序遍历二叉树。
    • 特点：首先访问根节点，然后递归地前序遍历左子树，最后递归地前序遍历右子树。
    • 应用：常用于复制一棵树、计算表达式的值等。

  2. 中序遍历：

    • 特点：按照“左-根-右”的顺序遍历二叉树。
    • 特点：先递归地中序遍历左子树，然后访问根节点，最后递归地中序遍历右子树。
    • 应用：常用于二叉搜索树，可以得到一个递增的有序序列。

  3. 后序遍历：

    • 特点：按照“左-右-根”的顺序遍历二叉树。
    • 特点：先递归地后序遍历左子树，然后递归地后序遍历右子树，最后访问根节点。
    • 应用：常用于释放二叉树的内存空间，或者计算表达式的值。

    例如：

四、二叉树的基本操作

我先把主函数给出，接下来就将按照主函数中的这些功能一步一步来实现

int main()
{
	Tree* root = CreatTree();
	//前序
	printf("前序：");
	PrevTree(root);
	printf("\n");
	//中序
	printf("中序：");
	HalfTree(root);
	printf("\n");
	//后序
	printf("后序：");
	PostTree(root);
	printf("\n");
	//节点个数
	int count = BTreeSize(root);
	printf("BTreeSize:%d\n", count);
	//叶子节点个数
	printf("BTreeLeafSize:%d\n", BTreeLeafSize(root));
	//树的高度
	printf("BTreeHigh:%d\n", BTreeHigh(root));
	//二叉树第k层节点个数
	printf("BTreeLevelKSize:%d\n", BTreeLevelKSize(root, 3));
	//二叉树查找值为x的节点
	

    return 0;
}

1、创建二叉树

//二叉树
typedef int TreeDataType;
typedef struct Tree
{
	TreeDataType a;
	struct Tree* left;
	struct Tree* right;
}Tree;
//初始化二叉树
Tree* TreeInit(TreeDataType x)
{
	Tree* m = (Tree*)malloc(sizeof(Tree));
	if (m == NULL)
	{
		perror("TreeInit");
		return NULL;
	}
	m->a = x;
	m->left = NULL;
	m->right = NULL;
	return m;
}
//创建一个二叉树
Tree* CreatTree()
{
	Tree* n1 = TreeInit(3);
	Tree* n2 = TreeInit(5);
	Tree* n3 = TreeInit(6);
	Tree* n4 = TreeInit(7);
	Tree* n5 = TreeInit(9);

	n1->left = n2;
	n1->right = n3;
	n2->left = n4;
	n2->right = n5;

	return n1;
}

2、前序、中序、后序

前序、中序和后序其实就是数据按照上面图片中的形式进行遍历

//前序
void PrevTree(Tree* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	printf("%d ", root->a);
	PrevTree(root->left);
	PrevTree(root->right);
}
//中序
void HalfTree(Tree* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	HalfTree(root->left);
	printf("%d ", root->a);
	HalfTree(root->right);
}
//后序
void PostTree(Tree* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	PostTree(root->left);
	PostTree(root->right);
	printf("%d ", root->a);
}

运行结果：

3、求二叉树的节点个数

//二叉树节点个数
int BTreeSize(Tree* root)
{
	//分治的思想
	if (root == NULL)
	{
		return 0;
	}
	return BTreeSize(root->left) + BTreeSize(root->right)+1 ;
}

用到了递归的思想，下面的内容都要用递归来解决，如果递归学的不太好建议画图来看这些过程如何进行的

运行结果：

4、求二叉树叶子节点的个数

//二叉树叶子节点个数
int BTreeLeafSize(Tree* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	return BTreeLeafSize(root->left) + BTreeLeafSize(root->right);
}

运行结果：

5、树的高度

//求二叉树高度
int BTreeHigh(Tree* root)
{
	if (root == NULL)
	{
		return 0;
	}
	int leftHigh = BTreeHigh(root->left);
	int rightHigh = BTreeHigh(root->right);

	return leftHigh > rightHigh ? leftHigh + 1 : rightHigh + 1;
}

运行结果：

6、二叉树第k层的节点个数

//二叉树第k层节点个数
int BTreeLevelKSize(Tree* root, int k)
{
	assert(k > 0);
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	return BTreeLevelKSize(root->left, k - 1) + BTreeLevelKSize(root->right, k - 1);
}

运行结果：

7、二叉树查找值为x的节点

//二叉树查找值为x的节点
Tree* BTreeFind(Tree* root,int x)
{
	if (root == NULL)
		return NULL;
	if (root->a == x)
		return root;
	Tree* ret1 = BTreeFind(root->left, x);
	if (ret1)
	{
		return ret1;
	}
	Tree* ret2 = BTreeFind(root->right, x);
	if (ret2)
	{
		return ret2;
	}
}

五、完整代码实例

//二叉树
typedef int TreeDataType;
typedef struct Tree
{
	TreeDataType a;
	struct Tree* left;
	struct Tree* right;
}Tree;
//初始化二叉树
Tree* TreeInit(TreeDataType x)
{
	Tree* m = (Tree*)malloc(sizeof(Tree));
	if (m == NULL)
	{
		perror("TreeInit");
		return NULL;
	}
	m->a = x;
	m->left = NULL;
	m->right = NULL;
	return m;
}
//创建一个二叉树
Tree* CreatTree()
{
	Tree* n1 = TreeInit(3);
	Tree* n2 = TreeInit(5);
	Tree* n3 = TreeInit(6);
	Tree* n4 = TreeInit(7);
	Tree* n5 = TreeInit(9);

	n1->left = n2;
	n1->right = n3;
	n2->left = n4;
	n2->right = n5;

	return n1;
}
//前序
void PrevTree(Tree* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	printf("%d ", root->a);
	PrevTree(root->left);
	PrevTree(root->right);
}
//中序
void HalfTree(Tree* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	HalfTree(root->left);
	printf("%d ", root->a);
	HalfTree(root->right);
}
//后序
void PostTree(Tree* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	PostTree(root->left);
	PostTree(root->right);
	printf("%d ", root->a);
}
//二叉树节点个数
int BTreeSize(Tree* root)
{
	//分治的思想
	if (root == NULL)
	{
		return 0;
	}
	return BTreeSize(root->left) + BTreeSize(root->right)+1 ;
}
//二叉树叶子节点个数
int BTreeLeafSize(Tree* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	return BTreeLeafSize(root->left) + BTreeLeafSize(root->right);
}
//求二叉树高度
int BTreeHigh(Tree* root)
{
	if (root == NULL)
	{
		return 0;
	}
	int leftHigh = BTreeHigh(root->left);
	int rightHigh = BTreeHigh(root->right);

	return leftHigh > rightHigh ? leftHigh + 1 : rightHigh + 1;
}
//二叉树第k层节点个数
int BTreeLevelKSize(Tree* root, int k)
{
	assert(k > 0);
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	return BTreeLevelKSize(root->left, k - 1) + BTreeLevelKSize(root->right, k - 1);
}
//二叉树查找值为x的节点
Tree* BTreeFind(Tree* root,int x)
{
	if (root == NULL)
		return NULL;
	if (root->a == x)
		return root;
	Tree* ret1 = BTreeFind(root->left, x);
	if (ret1)
	{
		return ret1;
	}
	Tree* ret2 = BTreeFind(root->right, x);
	if (ret2)
	{
		return ret2;
	}
}
int main()
{
	Tree* root = CreatTree();
	//前序
	printf("前序：");
	PrevTree(root);
	printf("\n");
	//中序
	printf("中序：");
	HalfTree(root);
	printf("\n");
	//后序
	printf("后序：");
	PostTree(root);
	printf("\n");
	//节点个数
	int count = BTreeSize(root);
	printf("BTreeSize:%d\n", count);
	//叶子节点个数
	printf("BTreeLeafSize:%d\n", BTreeLeafSize(root));
	//树的高度
	printf("BTreeHigh:%d\n", BTreeHigh(root));
	//二叉树第k层节点个数
	printf("BTreeLevelKSize:%d\n", BTreeLevelKSize(root, 3));
	//二叉树查找值为x的节点
	

    return 0;
}

运行结果：

总结

总而言之，二叉树其实是对我们运用递归来遍历数据的考察，由于篇幅原因，这里我们只对二叉树的结构进行了大致的讲解，有不理解的地方欢迎与我私信或者在评论区中指出

创作不易，还请各位大佬点个小小的赞！！！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1574757.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【前端Vue】Vue3+Pinia小兔鲜电商项目第4篇：静态结构搭建和路由配置,1. 准备分类组件【附代码文档】

【前端Vue】Vue3+Pinia小兔鲜电商项目第4篇：静态结构搭建和路由配置,1. 准备分类组件【附代码文档】

Vue3ElementPlusPinia开发小兔鲜电商项目完整教程（附代码资料）主要内容讲述：认识Vue3，使用create-vue搭建Vue3项目1. Vue3组合式API体验,2. Vue3更多的优势,1. 认识create-vue,2. 使用create-vue创建项目,1. setup选项的写法和执行…
阅读更多...
C语言解决汉诺塔问题

C语言解决汉诺塔问题

背景 首先带大家了解一下汉诺塔问题 汉诺塔是一个典型的函数递归问题，汉诺塔描述了这样的场景，有三个柱子，A,B,C，A柱为起始柱，在A柱上面有若干大小不同的盘子，最下面的最大，最上面的最小&#x…
阅读更多...
Linux系统下安装ElasticSearch

Linux系统下安装ElasticSearch

一、228环境ES使用安装 1、检验ES服务是否安装成功的方法 （1）查看Elasticsearch进程是否成功 ps -ef|grep elasticsearch （2）linux elasticsearch下访问（curl带认证访问） curl --user elastic:Zhes.13…
阅读更多...
CSS面试题常用知识总结day03

CSS面试题常用知识总结day03

大家好我是没钱的君子下流坯，用自己的话解释自己的知识 前端行业下坡路，甚至可说前端已死，我还想在前段行业在干下去，所以从新开始储备自己的知识。 从CSS——>Javascript——>VUE2——>Vuex、VueRouter、webpack——>…
阅读更多...
STM32F103C8T6-CAN

STM32F103C8T6-CAN

本文内容 HAL库下printf重定向解决问题：Keil下调试可以正常运行，而下载后运行不了CAN总线的回环测试，自发自收 printf重定向 实现printf重定向的目的是方便调试，通过UART查看打印的调试信息。 下面以STM32F103C8T6为例&#xf…
阅读更多...
【前沿模型解析】潜在扩散模 1 | LDM第一阶段-感知图像压缩总览

【前沿模型解析】潜在扩散模 1 | LDM第一阶段-感知图像压缩总览

文章目录 0 开始~1 感知压缩的目的2 自回归编码器-解码器生成模型一览2.1 AE 自编码器2.2 VAE 变分自编码器2.3 VQ-VAE2.4 VQ-GAN 3 代码部分讲解总览 0 开始~ 从今天起呢，我们会剖析LDM（潜在扩散模型） 从去年开始，大量的生成模…
阅读更多...
数学建模-------MATLAB分支循环断点调试

数学建模-------MATLAB分支循环断点调试

1.if语句 （1）分段函数的引入（这里的数据表示的是分数的不同区间对应的等级） (1)这个就是一个十分简单的if语句，无论是if还是elseif后面都是不能添加任何分号的，这个例子就是一个分段的函数，在不…
阅读更多...
基础总结篇：Activity生命周期

基础总结篇：Activity生命周期

private int param 1; //Activity创建时被调用 Override public void onCreate(Bundle savedInstanceState) { super.onCreate(savedInstanceState); Log.i(TAG, “onCreate called.”); setContentView(R.layout.lifecycle); Button btn (Button) findViewById(R.id.…
阅读更多...
医药行业痛点以及OKR解决方案

医药行业痛点以及OKR解决方案

一、背景 随着医药行业的快速发展和市场竞争的加剧，企业面临着前所未有的挑战和机遇。为了在激烈的市场竞争中立于不败之地，某知名医药企业决定引入OKR（Objectives and Key Results，目标与关键成果）管理模式&#xff0…
阅读更多...
Gradle入门初探

Gradle入门初探

一、Gradle简介： 我们都创建过基于Maven的项目，maven可以很好的管理项目的依赖，编译和打包项目，Gradle是一个和Maven类似的自动化构建工具，Maven是基于xml文件格式，而Gradle是基于Groovy的语言&#xff0c…
阅读更多...
dm8数据迁移工具DTS

dm8数据迁移工具DTS

dm8数据迁移工具DTS DTS工具介绍 DM数据迁移工具提供了主流大型数据库迁移到DM、DM到DM、文件迁移到DM以及DM迁移到文件的功能。DM数据迁移工具采用向导方式引导用户通过简单的步骤完成需要的操作。 DM数据迁移工具支持： ◆ 主流大型数据库Oracle、SQLServer、MyS…
阅读更多...
Advanced RAG 01：讨论未经优化的 RAG 系统存在的问题与挑战

Advanced RAG 01：讨论未经优化的 RAG 系统存在的问题与挑战

编者按： 自 2023 年以来，RAG 已成为基于 LLM 的人工智能系统中应用最为广泛的架构之一。由于诸多产品的关键功能严重依赖RAG，优化其性能、提高检索效率和准确性迫在眉睫，成为当前 RAG 相关研究的核心问题。 我们今天为大家带来的这…
阅读更多...
【无标题】【Android】Android中Intent的用法总结

【无标题】【Android】Android中Intent的用法总结

2.显示地图: Java代码 Uri uri Uri.parse(“geo:38.899533,-77.036476”); Intent it new Intent(Intent.Action_VIEW,uri); startActivity(it); 3.从google搜索内容 Java代码 Intent intent new Intent(); intent.setAction(Intent.ACTION_WEB_SEARCH); intent.pu…
阅读更多...
SAP操作教程第16期：SAP B1关于审批模块的设置

SAP操作教程第16期：SAP B1关于审批模块的设置

工作效率是企业的生存之本，也是员工能够在企业中发展之本。自动化和规范化的审批流程可以减少手动操作以及沟通环节、节约时间和资源从而提高工作效率。 所以，今天我们就一起来了解一下SAP B1中关于审批模块的设置。 01关于审批模块的设置 第一步&#x…
阅读更多...
数据结构基础：双链表结构、实现

数据结构基础：双链表结构、实现

继续和颦颦学C语言呀.......> 双链表的结构 这里的head 为头节点，是‘哨兵位’，实际不存储任何有效的数据 它的存在是为了遍历环链表避免死循环 双链表的实现 typedef int LTDataType; typedef struct ListNode { struct ListNode* next; //指针保存…
阅读更多...
为什么使用MQ？？？？

为什么使用MQ？？？？

1、异步处理 场景说明：用户注册后，需要发注册邮件和注册短信,传统的做法有两种 1.串行的方式 2.并行的方式。 串行方式: 将注册信息写入数据库后,发送注册邮件,再发送注册短信,以上三个任务全部完成后才返回给客户端。 这有一个问题是,邮件,短信并不是…
阅读更多...
2024/4/1—力扣—二叉树的最近公共祖先

2024/4/1—力扣—二叉树的最近公共祖先

代码实现： 思路： 递归判断左子树和右子树，查找p或者q是否在当前节点的子树上 1，在同一子树上，同一左子树，返回第一个找到的相同值，同一右子树上，返回第一个找到的相同值 2&#xff0…
阅读更多...
【每日刷题】Day4

【每日刷题】Day4

【每日刷题】Day4 🥕个人主页：开敲🍉 🔥所属专栏：每日刷题🍍 目录 1. 83. 删除排序链表中的重复元素 - 力扣（LeetCode） 2. 88. 合并两个有序数组 - 力扣（LeetCode&…
阅读更多...
Windows SDK（六）组合框与列表框控件

Windows SDK（六）组合框与列表框控件

组合框和列表框同样也是控件，所以我们在应用组合框和列表框时同样也需要父窗口，现在我们以 创建项目时程序自行创建的窗口作为父窗口展开如下的控件创建与应用 在进行组合框与列表框的讲解前，我们首先在程序中定义几个宏作为我们在编写程序…
阅读更多...
C语言：顺序表专题

C语言：顺序表专题

目录 一、数据结构之顺序表/链表1.数据结构相关概念1.1什么是数据结构1.2为什么需要数据结构 二、顺序表1.顺序表的概念及结构2.顺序表分类3.动态顺序表的实现 一、数据结构之顺序表/链表 1.数据结构相关概念 1.1什么是数据结构 数据结构是由“数据”和“结构”两词组合而来…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023