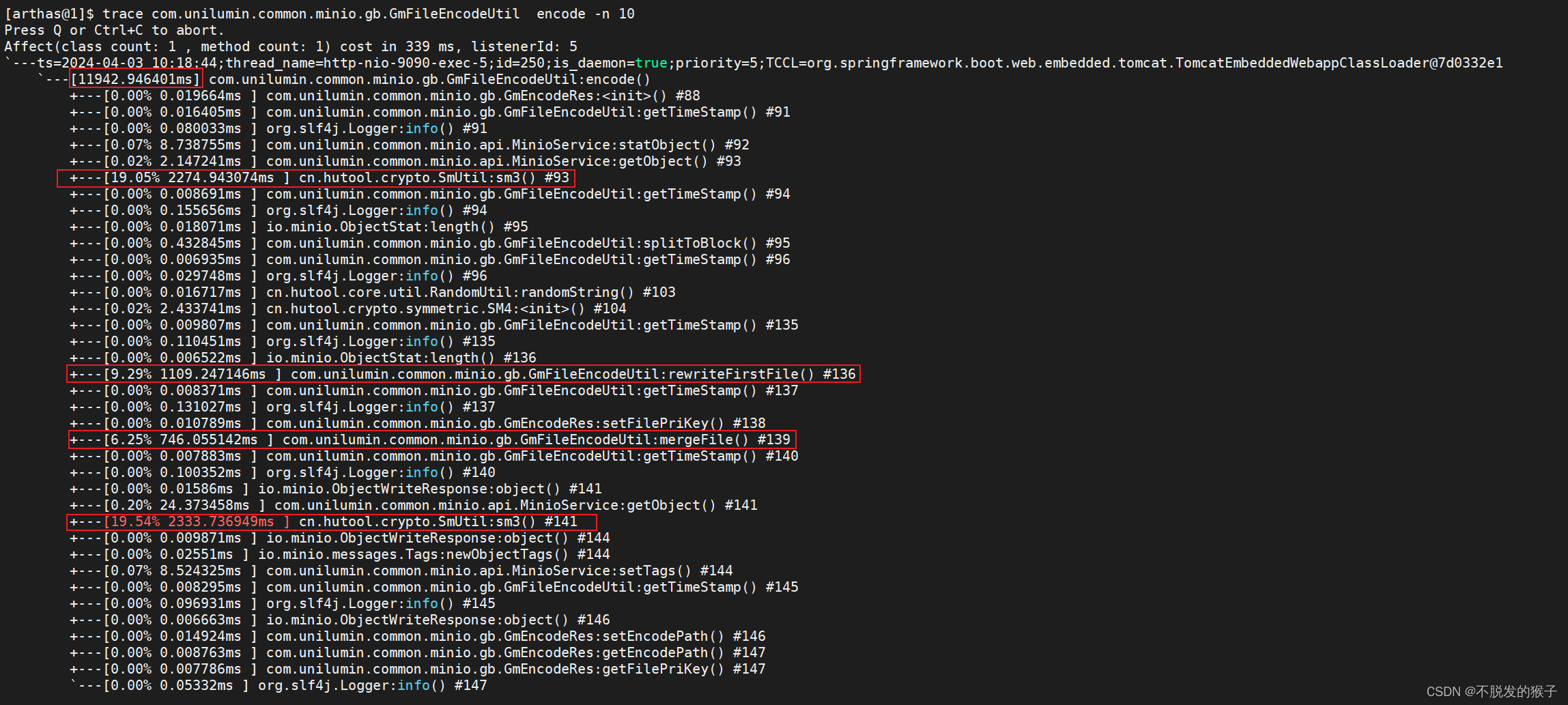
本文架构
- 零、前言
- 一、KLEE简介
- 二、Docker安装KLEE
- 1. 使用apt安装docker
- 2.拉取klee镜像
- 3.使用git 拉取klee源码
- 4.安装klee镜像
- 5. 运行镜像
- 三、试用KLEE的examples
- 1.查看并了解待测文件`examples/get_sign/get_sign.c`
- 2.KLEE进行符号测试的基本步骤
- 编译成LLVM位码文件
- 使用KLEE进行符号执行
- 查看生成的测试用例
- ktest中结果解释
- 四、使用KLEE生成的测试用例运行程序
- 1.链接到klee库
- 2.查看执行结果
- 五、约束文件生成
- 1.生成约束文件
- 查看`all:kquery`格式文件
- 查看`solver:Kquery`格式文件
- 2.约束文件的结构
- 基本结构
- 详细结构
零、前言
反复试了几个源码安装KLEE的教程都不行,装了一天毫无进展,几乎怀疑人生。后来想反正我不需要在KLEE基础上再开发,就直接使用Docker安装KlEE就好了。
在这个基础上进一步写(原文链接),原文写的挺好的,但就是写作格式需要改进 -v-。
一、KLEE简介

符号执行 (Symbolic Execution) 是一种程序分析技术,其可以通过分析程序来得到让特定代码区域执行的输入。使用符号执行分析一个程序时,该程序会使用符号值作为输入,而非一般执行程序时使用的具体值。在达到目标代码时,分析器可以得到相应的路径约束,然后通过约束求解器来得到可以触发目标代码的具体值。
相关可阅读文献(仅供参考)
1.【OSDI 2008-Cristian Cadar et al. 】《KLEE: Unassisted and Automatic Generation of High-Coverage Tests for Complex Systems Programs》
2.【Github】KLEE
3.【官网】KLEE Symbolic Execution Engine
4.【Github Blog】符号执行, KLEE 与 LLVM
5.【个人网站】符号执行引擎 KLEE 学习笔记
6.【官方文档】KLEE Doc
二、Docker安装KLEE
1. 使用apt安装docker
# ubuntu安装docker
sudo apt install docker
sudo apt install docker.io
2.拉取klee镜像
docker pull klee/klee

3.使用git 拉取klee源码
git clone https://github.com/klee/klee.git
4.安装klee镜像
cd klee
# 注意,klee/klee后面那个“.” 记得加上,表示在当前路径下创建一个镜像
# docker build <OPTIONS> PATH | URL | -
docker build -t klee/klee .
此处会进行大约几分钟的安装,基本都是环境的下载。

5. 运行镜像
docker run 命令详解这个文章写的比较好【CSDN Blog】docker run 命令详解(新手入门必备)
docker run --rm -ti --ulimit=‘stack=-1:-1’ klee/klee
运行容器成功后可以看到已经有了klee的src和build目录

此时可以正常使用klee,例如运行klee里面的example,简单体验klee
三、试用KLEE的examples
1.查看并了解待测文件examples/get_sign/get_sign.c
cd klee_src/examples/get_sign
vim get_sign.c

此函数目的十分简单,判断一个数是正、负还是0。
- 可以看到
main函数中klee_make_symbolic()函数,该函数包含在头文件klee.h中,主要是将一个值替换成符号形式,以对其进行符号执行。 - 该函数接收3个参数:<
变量地址、变量大小、变量名>(可以为任何值)。 main函数目的:将变量a符号化并用它调用get_sign()
2.KLEE进行符号测试的基本步骤
编译成LLVM位码文件
由于klee是对LLVM IR进行实现的,所以需要将待测文件编成LLVM位码文件先。运行指令:
clang -I ../../include -emit-llvm -c -g -O0 -Xclang -disable-O0-optnone get_sign.c
参数解释
| 参数 | 解释 |
|---|---|
-I<dir> | 添加目录到include搜索路径,这样我们的编译器才能找到klee/klee.h,里面定义了很多我们需要与klee虚拟机进行交互的内部函数,比如klee_make_symbolic |
-emit-llvm | 对汇编程序和对象文件使用LLVM表示。 |
-c | 只运行预处理、编译和汇编步骤。 |
-g | 将调试信息添加到位代码文件中,以便之后使用该文件生成源代码行级别的统计信息。如果没有这个参数,将无法得到映射在源码层面的一些信息,不方便我们查看结果。 |
-O0 -Xclang -disable-O0-optnone | 这个是一些优化相关的问题,O0表示不进行任何优化.因为我们需要对源码进行符号执行,所以源码的结构信息是十分重要的,部分编译器进行优化可能会丧失这种结构信息。 |
输入完成后得到get_sign.bc

使用KLEE进行符号执行
使用klee对bc文件进行符号执行。原文链接。但不是很详细,重新做个笔记。
klee get.sign.bc

可以看到:
- KLEE一共执行了33条指令,探索了3条执行路径,生成了3条测试用例
- 新生成了
klee-last和klee-out-0文件夹。输出结果报告放在了klee-out-0(或者klee-last)目录下(PS:klee每执行一次都会生成一个klee-out-N,其中N是表示第几次的执行,这里我们只执行了一次,因此是0。除此之外,会生成一个klee-last的符号链接,指向最新生成的这个k查看Klee-out-N)。
使用ll也可以看到klee-last是一个指向最新生成测试文件文件夹的软链接。

我们查看下目录 klee-last

各个文件的作用可以见【官方文档】
查看生成的测试用例
查看测试用例需要使用klee-tools,这里我们分别查看下test0000001.ktest,test0000002.ktest,test0000003.ktest。

ktest中结果解释
图中可见,其生成的三个测试用例有符号整型值分别对应0,16843009,-2147483648。
| 参数 | 参数解释 |
|---|---|
args | 调用程序时使用的参数,这个例子中只有程序名 |
num objects: | 符号对象在路径上的数量,在这个例子中只有1个 |
object 0: name: | 符号对应的变量名字 |
object 0:size: | 符号对应的变量大小 |
object 0:int\hex\uint等: | 其他格式的用例查看。例如:无符号形式uint、十六进制hex |
四、使用KLEE生成的测试用例运行程序
1.链接到klee库
用klee提供的库来将得到的测试用例作为输入来运行我们的程序。首先将我们的程序链接到klee提供的库libkleeRuntest
export LD_LIBRARY_PATH=<KLEE_BUILD_PATH/lib>:$LD_LIBRARY_PATH
# 指定将get_sign.c编成 get_sign.out
$ gcc -I ../../include -L <KLEE_BUILD_PATH/lib>/lib get_sign.c -o get_sign -lkleeRuntest
# 使用默认,生成a.out
$ gcc -I ../../include -L <KLEE_BUILD_PATH/lib>/lib get_sign.c -lkleeRuntest
这里的KLEE_BUILD_PATH是你KLEE的build目录,请根据自己的实际设置。

2.查看执行结果
两个指令生成的就是文件名不一样。将测试用例输入程序a.out或者get_sign.out
KTEST_FILE=klee-last/test000001.ktest ./a.out
# 或者
KTEST_FILE=klee-last/test000001.ktest ./get_sigin.out.out
使用echo $?输出执行结果,可以看到测试用例1的值为0 所以函数执行后同样输出0。其他的东西都一样,就不逐一试了。

五、约束文件生成
我使用KLEE的目的就是为了获取程序分析后的约束文件,所以这里也写下。只找到一篇文章【简书Blog】KLEE中的约束文件解析。但本文跟它存在偏差。约束文件的格式讲解可以参靠这篇文章。
更多的内容还是来自官方文档
The reference manual for the KQuery language
1.生成约束文件
在进行符号执行前添加相关参数(这里与原文章介绍的-use-query-log=all:pc不一样,可能版本不同,所以大家最好还是通过输入klee --help来查看自己当前版本的参数是什么)
| 参数 | 参数解释 |
|---|---|
-use-query-log=all:kquery | 记录格式为KQuery,全部约束 |
-use-query-log=all:smt2 | 记录格式为SMT-LIBv2,全部约束 |
-use-query-log=solver:kquery | 记录格式为KQuery ,只记录交于约束求解器求解的约束 |
-use-query-log=solver:smt2 | 记录格式为SMT-LIBv2,solver则表示只记录交于约束求解器求解的约束 |
输入命令
klee -use-query-log=all:kquery get_sign.bc
可以看到生成了名为all-queries.kquery文件

查看all:kquery格式文件
使用vim查看all:kquery格式文件
vim all-queries.kquery

一共生成了4个约束条件。
查看solver:Kquery格式文件
klee -use-query-log=solver:kquery get.sign.bc
vim solver-queries.kquery

可以看到最终交给约束求解器求解的一共只有3个。
2.约束文件的结构
基本结构
kquery = { array-declaration | query-command }
- 数组声明(array-declaration):用于声明在后续表达式中使用的位向量数组。
- 查询命令(query-command):用于定义应由约束求解器执行的查询。查询由一组约束(假设)、一个查询表达式以及可选的表达式和数组组成,用于在查询表达式无效时计算值。
详细结构
一般一个求解的查询命令包括5个元素:元素1为关键字"query";元素2个由[]包裹,表示一个待解约束表达式列表 ;元素3表示期望元素2合取后不满足的布尔值(即求得的解使得元素2与元素3不等);元素4由[]包裹,表示约束求解过程中,要顺带计算的表达式列表,如果元素5不存在,元素4可以不存在;如果元素5存在,又没有什么表达式需要计算时,此处应为[];元素5由[]包裹,表示元素2中需要求解的变量列表. --------引自《【简书Blog】KLEE中的约束文件解析》
简单说就是:
query
[元素2: 待求解表达式列表]
<元素3:元素2解析后不满足时布尔值>
[元素4:求解过程中需要计算的表达式,可为空]
[元素5:元素2中需要求解的变量列表]