算法基础课-搜索与图论

DFS

题目链接：842. 排列数字 - AcWing题库
思路：写的很好的题解AcWing 842. 排列数字--深度优先遍历代码+注释 - AcWing

#include<bits/stdc++.h>

using namespace std;
int n;
int st[10];
vector<int> a;
void dfs(){
    if(a.size() == n){
        for(int i=0;i<n;i++){
            cout<<a[i]<<" ";
        }
        cout<<endl;
    }
    for(int i=1;i<=n;i++){
        if(!st[i]){
            
            a.push_back(i);
            st[i] = true;
            dfs();
            a.pop_back();
            st[i] = false;
            
        }
    }
}

int main()
{
    cin>>n;
    dfs();
    
    return 0;
}

也可以考虑使用c++自带的next_permutation函数直接秒了：

#include<bits/stdc++.h>
using namespace std;
vector<int> a;
int n;
int st[10];

int main(){
	cin>>n;
	for(int i=0;i<n;i++) st[i] = i+1;
	do{
		for(int i=0;i<n;i++) cout<<st[i]<<" ";
		cout<<endl;
	}while(next_permutation(st,st+n));
	return 0;
}

BFS

题目链接：844. 走迷宫 - AcWing题库

思路：由于bfs是一层一层扩展，所以能保证走到终点时，走过的距离最短，所以不需要取min。可以在bfs中判断一下，走到终点直接输出终点的distance。

#include<bits/stdc++.h>
#define x first
#define y second
using namespace std;
typedef pair<int,int> PII;
int n,m;
const int N = 110;
int g[N][N];
int dist[N][N];
int dx[4]={0,1,0,-1},dy[4]={1,0,-1,0};
// int st[N][N];
void bfs(int x,int y){
    queue<PII> q;
    q.push({x,y});
    dist[0][0] = 0;
    // st[x][y] = true;
    while(q.size()){
        auto t = q.front();
        q.pop();
        int x = t.x,y = t.y;
        for(int i=0;i<4;i++){
            int tx = x + dx[i];
            int ty = y + dy[i];
            if(g[tx][ty] == 1) continue;
            if(tx<0||tx>=n||ty<0||ty>=m) continue;
            // if(st[tx][ty]) continue;
            // st[tx][ty] = true;
            g[tx][ty] = 1;
            dist[tx][ty] = min(dist[tx][ty],dist[x][y]+1);
            q.push({tx,ty});
            // cout<<tx<<" "<<ty<<endl;
        }
    }
}
int main(){
    cin>>n>>m;
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++) cin>>g[i][j];
    }
    memset(dist,0x3f,sizeof dist);
    bfs(0,0);
    cout<<dist[n-1][m-1];
    return 0;
}

树与图的深度优先遍历

题目链接：1207. 大臣的旅费 - AcWing题库

思路：题意是求树的直径（树中两个最远结点的距离），可以随机找一个点0，走到距离0点最远的点1，再从这个点1走到距离点1最远的点2，此时点1距离点2的距离就是树的直径。

图的存储与遍历参考：B02 图的存储_哔哩哔哩_bilibili

#include<bits/stdc++.h>
#define x first 
#define y second 

using namespace std;
const int N = 100010;
typedef pair<int,int> PII;
vector<PII> h[N];
int dist[N];
void dfs(int u,int father,int distance){
    dist[u] = distance;
    
    for(auto t:h[u]){
        if(t.x!=father){
            dfs(t.x,u,distance+t.y);
        }
    }
    
}

int main(){
    int n ;
    cin>>n;
    for(int i=0;i<n-1;i++){
        int x,y,d;
        cin>>x>>y>>d;
        h[x].push_back({y,d});
        h[y].push_back({x,d});
    }
    
    dfs(1,-1,0);
    int u = 1;
    for(int i=1;i<=n;i++){
        if(dist[i]>dist[u]){
            u = i;
        }
    }
    dfs(u,-1,0);
    for(int i=1;i<=n;i++){
        if(dist[i]>dist[u]){
            u = i;
        }
    }
    
    int s = dist[u];

    printf("%lld\n", s * 10 + s * (s + 1ll) / 2);

    return 0;
}

树与图的广度优先遍历

题目链接：847. 图中点的层次 - AcWing题库

思路：h数组表示邻接表，下标表示结点编号，每个vector存储的是每个结点能到达的节点。

这个老师讲的超级好。B02 图的存储_哔哩哔哩_bilibili

#include<bits/stdc++.h>

using namespace std;
const int N = 100010;
vector<int> h[N];
bool st[N];
int dist[N];
int n,m;
void bfs(int u){
    queue<int> q;
    q.push(u);
    st[u] = true;
    dist[u] = 0;
    while(q.size()){
        int t = q.front();
        q.pop();
        if(t == n){
            cout<<dist[t];
            return;
        }
        for(int i=0;i<h[t].size();i++){
            int ne = h[t][i];
            if(st[ne]) continue;
            
            st[ne] = true;
            q.push(ne);
            dist[ne] = dist[t] + 1;
        }
    }
    cout<<-1<<endl;
    return;
}
int main(){
    cin>>n>>m;
    for(int i=0;i<m;i++){
        int a,b;
        cin>>a>>b;
        h[a].push_back(b);
    }
    memset(dist,-1,sizeof dist);
    bfs(1);
    return 0;
}

拓扑排序

题目链接：848. 有向图的拓扑序列 - AcWing题库
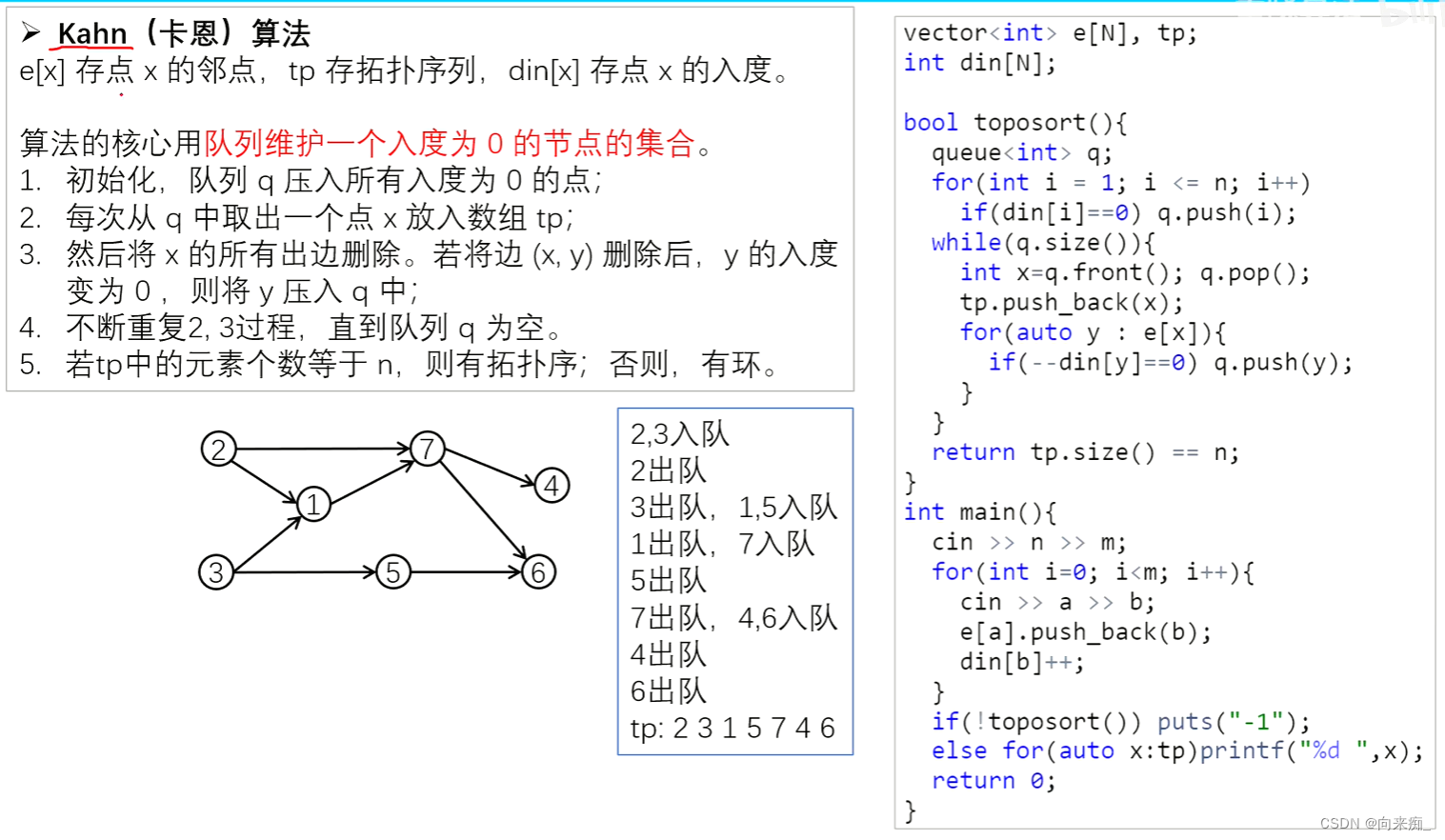
思路：跟bfs有些相似，先找入度为零的点加入到队列当中，再枚举当前结点出边，减少出边元素的入度，当入度为0时加入到拓扑序列中，这里是当出队的时候加入到序列中，跟bfs更像了。

这个老师讲的可好D01 拓扑排序_哔哩哔哩_bilibili。

#include<bits/stdc++.h>

using namespace std;
const int N = 100010;
vector<int> e[N],tp;
int din[N];

int n,m;
bool topsort(){
    queue<int> q;
    for(int i=1;i<=n;i++){
        if(din[i] == 0) q.push(i);
    }
    while(q.size()){
        auto t = q.front();
        q.pop();
        tp.push_back(t);
        for(auto y : e[t]){
            din[y]--;
            if(!din[y]) q.push(y);
        } 
    }
    return tp.size() == n;
}

int main(){
    cin>>n>>m;
    for(int i=0;i<m;i++){
        int a,b;
        cin>>a>>b;
        e[a].push_back(b);
        din[b]++;
    }
    if(topsort()){
        for(int i = 0;i<n;i++){
            cout<<tp[i]<<" ";
        }
    }else cout<<-1<<endl;
    
    return 0;
}

Dijkstra

朴素版

题目链接：849. Dijkstra求最短路 I - AcWing题库
思路：采取贪心的策略，对当前能到达的路径最短的点，使用其进行更新距离操作。

D02 最短路 Dijkstra 算法_哔哩哔哩_bilibili

#include<bits/stdc++.h>
#define x first
#define y second
using namespace std;
typedef pair<int,int> PII;
const int N = 510;
const int M = 1e5+10;
vector<PII> e[N];
int dist[N];
int n,m;
bool st[N];
void dijkstra(int s){
    dist[s] = 0;
    
    for(int i=1;i<n;i++){
        int u = 0;
        for(int i=1;i<=n;i++){
            if(!st[i]&&(dist[i]<dist[u] || u == 0)) u = i;
        }
        // cout<<u<<endl;
        st[u] = true;
        for(auto pr : e[u]){
            int v = pr.x, w = pr.y;
            if(dist[v]>dist[u]+w){
                dist[v] = dist[u] + w;
            }
        }
    }
}

int main(){
    cin>>n>>m;
    for(int i=0;i<m;i++){
        int a,b,w;
        cin>>a>>b>>w;
        e[a].push_back({b,w});
    }
    memset(dist,0x3f,sizeof dist);
    dijkstra(1);
    if(dist[n] == 0x3f3f3f3f) cout<<-1<<endl;
    else cout<<dist[n]<<endl;
    return 0;
}

堆优化版本

题目链接：850. Dijkstra求最短路 II - AcWing题库

思路：每次选秀选出当前最小的点，朴素版需要遍历寻找，堆优化版使用优先队列维护当前没有遍历到的距离最小的点，将每次选秀的遍历替换成取队列头部元素，从而降低时间复杂度。

需要注意的是为了维护优先队列中的顺序，存储的距离为负数。

D02 最短路 Dijkstra 算法_哔哩哔哩_bilibili

#include<bits/stdc++.h>
#define x first
#define y second
using namespace std;
int n,m;
typedef pair<int,int> PII;
const int N = 150010, M = 150010;
int dist[N];
priority_queue<PII> q;
vector<PII> h[N];
bool st[N];
void dijkstra(int s){
    dist[s] = 0;
    q.push({0,s});
    while(q.size()){
        PII p = q.top();
        int u = p.y;
        q.pop();
        if(st[u]) continue;
        st[u] = true;
        for(auto t : h[u]){
            int v = t.x, w = t.y;
            if(dist[v]>dist[u] + w){
                dist[v] = dist[u] + w;  //忘记更新距离
                q.push({-(dist[u]+w),v});
            }
        }
        
    }
}
int main(){
    cin>>n>>m;
    for(int i=0;i<m;i++){
        int a,b,c;
        cin>>a>>b>>c;
        h[a].push_back({b,c});
    }
    memset(dist,0x3f,sizeof dist);
    dijkstra(1);
    if(dist[n] == 0x3f3f3f3f) cout<<-1<<endl;
    else cout<<dist[n]<<endl;
    return 0;
}

bellman-ford

spfa

Floyd

题目链接：854. Floyd求最短路 - AcWing题库

思路：D04 最短路 Floyd 算法_哔哩哔哩_bilibili

#include<bits/stdc++.h>
using namespace std;
const int N = 210,INF = 1e9;
int n,m,Q;
int d[N][N];
void floyd(){
	for(int k=1;k<=n;k++){
		for(int i=1;i<=n;i++){
			for(int j=1;j<=n;j++){
				d[i][j] = min(d[i][j],d[i][k]+d[k][j]);
			}
		}
	}
}
int main(){
	cin>>n>>m>>Q;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			if(i==j) d[i][j] = 0;
			else d[i][j] = INF;
		}
	}	
	while(m--){
		int a,b,c;
		cin>>a>>b>>c;
		d[a][b] = min(d[a][b],c);
	}
	floyd();
	while(Q--){
		int a,b;
		cin>>a>>b;
		int t = d[a][b];
		if(t>INF/2) cout<<"impossible"<<endl;
		else cout<<t<<endl;
	}
	return 0;
}

Prim

题目链接：858. Prim算法求最小生成树 - AcWing题库

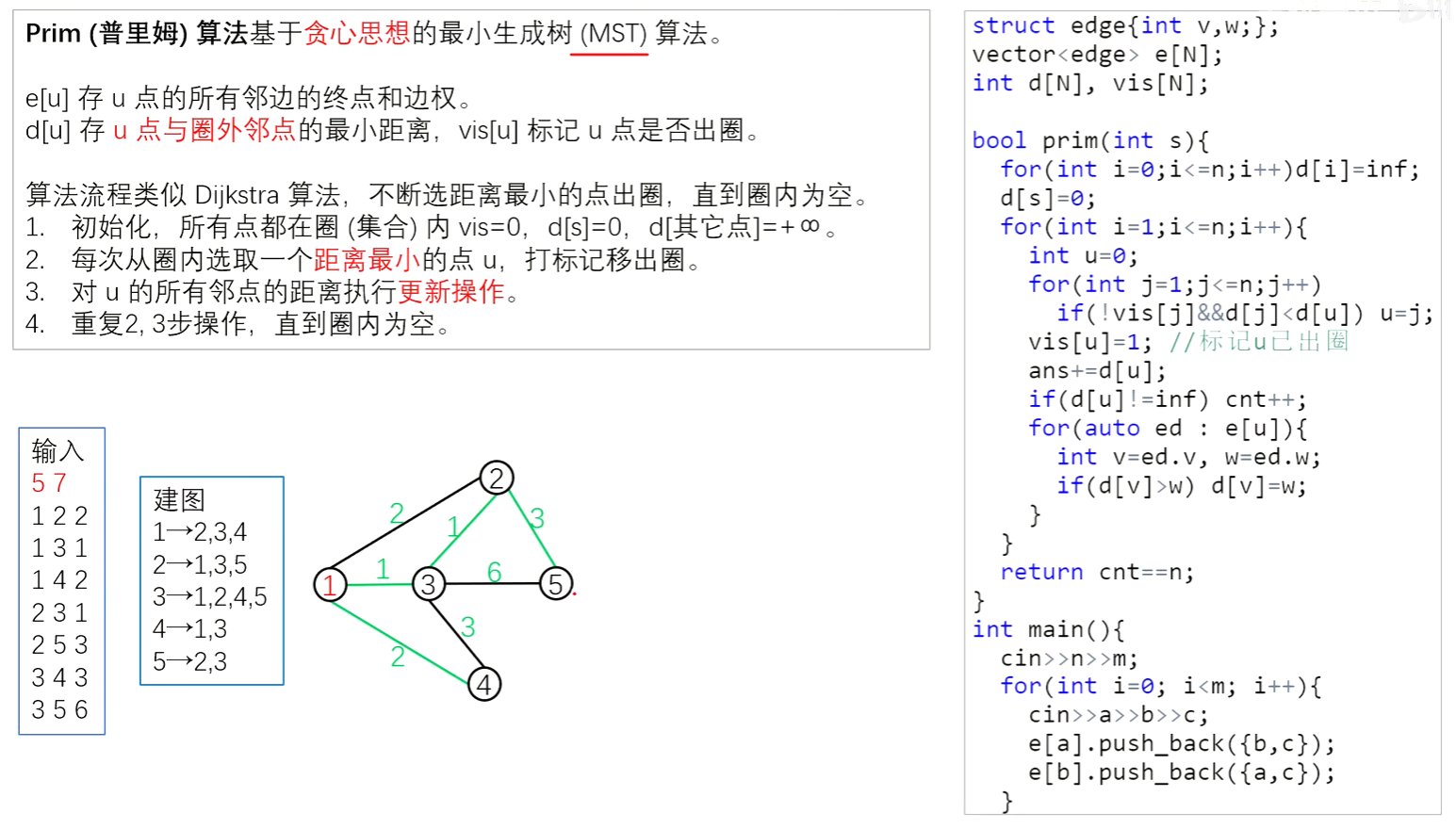
思路：D07 最小生成树 Prim 算法_哔哩哔哩_bilibili

和dijkstra一样，n次循环，每次选取最近的点来更新距离。

#include<bits/stdc++.h>
using namespace std;
const int N = 510,INF = 0x3f3f3f3f;
int n,m;
int g[N][N];
int dist[N];
bool st[N];
int prim(){
	memset(dist,0x3f,sizeof dist);
	int res = 0;
	for(int i=0;i<n;i++){
		int t = -1;
		for(int j=1;j<=n;j++){
			if(!st[j]&&(t==-1||dist[t]>dist[j]))
				t = j;
		}
		if(i && dist[t]==INF) return INF;
		if(i) res += dist[t];
		st[t] = true;
		for(int j=1;j<=n;j++) dist[j] = min(dist[j],g[t][j]);
	}
	return res;
}

int main(){
	cin>>n>>m;
	memset(g,0x3f,sizeof g);
	while(m--){
		int a,b,c;
		cin>>a>>b>>c;
		g[a][b] = g[b][a] = min(g[a][b],c);
	}
	int t = prim();
	if(t==INF) cout<<"impossible"<<endl;
	else cout<<t<<endl;
	return 0;
}

Kruskal

题目链接：859. Kruskal算法求最小生成树 - AcWing题库

思路：Kruskal算法是根据边求取最小生成树，先按边权排序，依次取权重最小的边，查看边的起点和终点是否在同一集合中（使用并查集），若不在同一集合，则将边加入到答案中，若在同一集合则继续循环。D08 最小生成树 Kruskal 算法_哔哩哔哩_bilibili

需要注意的是重载小于号的操作要记一下。

#include<bits/stdc++.h>
// #define x first
// #define y second
using namespace std;
// typedef pair<int,int> PII;
int n,m;
const int N = 1e5+10,M = 2e5+10;
struct edge{
    int u;int v;int w;
    bool operator<(const edge &t)const{
        return w<t.w;
    }
}e[M];
// vector<edge> e;
int fa[N];
int find(int x){
    if(x == fa[x]) return x;
    return fa[x] = find(fa[x]);
}
int main(){
    cin>>n>>m;
    for(int i=0;i<m;i++){
        int a,b,c;
        cin>>a>>b>>c;
        e[i] = {a,b,c};
    }
    int ans = 0;
    int cnt = 0;
    sort(e,e+m);
    for(int i=1;i<=n;i++) fa[i] = i;
    for(int i=0;i<m;i++){
        int u = e[i].u;
        int v = e[i].v;
        int w = e[i].w;
        if(find(u)!=find(v)){
            ans += w;   
            fa[find(u)] = find(v);
            cnt++;
        }
    }
    if(cnt == n-1) cout<<ans<<endl;
    else cout<<"impossible"<<endl;
    
    return 0;
}

染色法判定二分图

题目链接：860. 染色法判定二分图 - AcWing题库
思路：二分图的意思是看是否有能将所有节点分成两块，每块的节点中不能直接相连这样的情况存在。如下图中的1,4和2,3,5。根据定理：二分图中不存在奇环，我们可以由此判别一个图是否是二分图。D24 二分图判定染色法_哔哩哔哩_bilibili

老师使用的是链式前向星存储的图结构，具体思路如下。感觉直接用邻接表存储更好想，也更简便。

#include<bits/stdc++.h>

using namespace std;
int n,m;
const int N = 100010,M = 100010;
vector<int> h[N];
int color[N];
bool dfs(int u,int c){
    color[u] = c;
    for(auto t : h[u]){
        if(!color[t]){
            if(dfs(t,3-c)) return 1;
        }else if(color[t] == c) return 1;
    }
    return 0;
}

int main(){
    cin>>n>>m;
    for(int i=0;i<m;i++){
        int a,b;
        cin>>a>>b;
        h[a].push_back(b);
        h[b].push_back(a);
    }
    bool flag = false;
    for(int i =1;i<=n;i++){
        if(!color[i]){
            if(dfs(i,1)){
                flag = 1;
                break;
            }
        }
    }
    if(flag) puts("No");
    else puts("Yes");
    return 0;
    
}