目录

t检验

独立样本 t 检验

p值

spss如何分析独立样本t检验

配对样本t检验

单样本t检验

---

t检验

当我们想要比较两组数据（比如两组学生的成绩）是否真的有显著差异时，就可以使用 t 检验。

t 检验告诉我们，这种差异是不是真的很大，或者只是因为偶然的原因造成的。

就像是我们要判断一支队伍的比赛成绩是不是真的比另一支队伍更好一样，t 检验帮助我们找到答案。

独立样本 t 检验

独立样本 t 检验是一种统计方法，用于比较两组数据之间的平均值是否存在显著差异。这种检验适用于两组数据之间相互独立的情况，比如比较两个不同班级学生的考试成绩，或者比较两种不同药物治疗效果的研究。

通俗地说，就像是我们想知道两组人群（比如两个班级的学生）在某个方面（比如考试成绩）是否有显著差异，而独立样本 t 检验就像是一把放大镜，帮我们观察这个差异是否真的很显著，或者只是偶然发生的。

让我们来举一个例子来解释独立样本 t 检验。

假设有两个班级的学生，分别是班级 A 和班级 B。我们想知道两个班级的平均成绩是否有显著差异。

1. 首先，我们从班级 A 中随机选择了一些学生，并记录了他们的成绩数据。
2. 然后，我们从班级 B 中也随机选择了一些学生，并记录了他们的成绩数据。
3. 接下来，我们想知道，从这些数据中能否推断出两个班级的平均成绩是否真的有显著差异。
4. 因为，如果a平均分82，b平均分80，b班可能会说这是偶然情况，两班的成绩差异并不显著。

这时候，我们就可以使用独立样本 t 检验来进行分析。

在进行 t 检验时，我们会首先假设两个班级的平均成绩是相同的（这个假设叫做零假设），然后通过计算统计量（t 值）来判断是否支持这个假设。

如果计算出的 t 值足够大，意味着两个班级的平均成绩差异较大，那么我们就可以拒绝零假设，认为两个班级的平均成绩存在显著差异。

反之，如果计算出的 t 值不够大，那么我们就接受零假设，认为两个班级的平均成绩没有显著差异。

通过这样的方式，我们就可以利用独立样本 t 检验来判断两个班级的平均成绩是否有显著差异。

                                

p值

简单来说，p 值表示的是，在零假设为真的前提下，观察到当前样本数据或者更极端情况出现的概率。

如果 p 值很小，（小于设定的显著性水平 0.05），意味着我们得到的这个“（结果）结论是巧合”的概率小于5%，我们就有理由拒绝零假设，认为观察到的数据与零假设不一致，即存在显著性差异。

反之，如果 p 值较大，我们则不能拒绝零假设，认为观察到的数据与零假设一致，即不存在显著性差异。

好了，spss上号！

spss如何分析独立样本t检验

1）依次单击Analyze-Compare Means-Independent Samples T Test,打开独立样本t主对话框

2）选择检验变量和分组变量

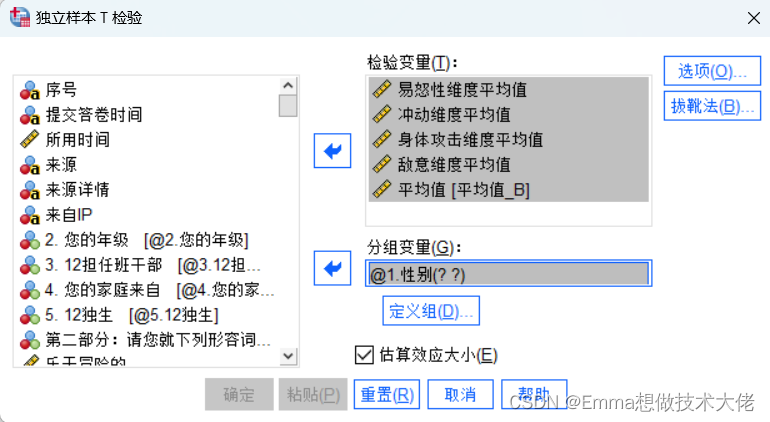
3）打开定义组

如果 Grouping Variable是分类变量且只有两个值,选择Use specified values 选项栏,在Group后面的参数框中分别键人两组的分类变量值;

如果Grouping Variable是分类变量且有多个值,选择Use specified values选项栏,并在Group后面的参数框中分别键人特定两组的分类变量值,系统只对具有这两个值的两个组进行均值比较;

如果GroupingVariable 是连续变量,选择 Cut point 选项并在其后面的参数栏中键入一个值,系统会将 Grouping Variable 按大于等于和小于该值分成两组,然后对它们进行均值比较。

4）点击ok。

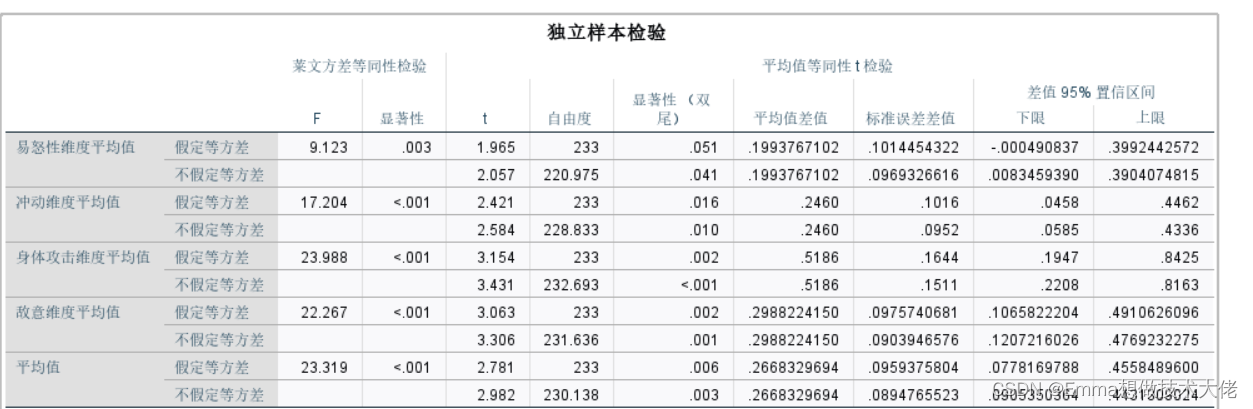
一般来说，如果显著性水平较小（比如p值小于0.05），并且其他检验结果也支持方差不齐的结论，那么就可以认为各组或样本的方差不齐。

那么就是看第二行（不假定方差）的显著性（双尾）来决定标不标星号

注：*p<0.05，**p<0.01，***p<0.001，下同。

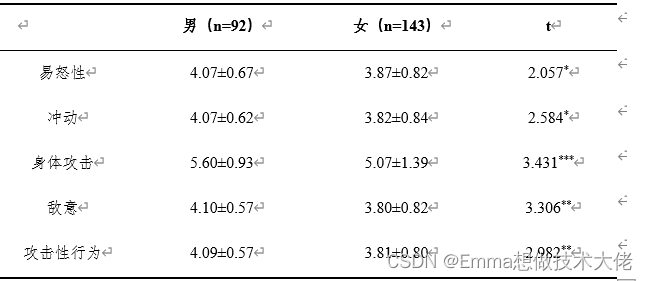
填上表就好了。

进行独立样本T检验结果发现：

大学生攻击性行为总分与其他各维度在该变量上均存在显著差异，男大学生得分显著高于女大学生。

                           

配对样本t检验

配对样本t检验是一种用于比较两组相关样本均值是否有显著差异的统计方法。

它适用于那些在不同时间点或者在不同条件下进行的观察，但是观察的对象是相同的情况。

                        

假设你是一位瑜伽老师，想要了解你的学生们在练习瑜伽前后心率是否有显著变化。

你随机选择了10名学生，让他们在瑜伽练习前测量心率，然后再进行一次练习后的测量。

现在你手里有两组数据：每个学生练习前的心率和练习后的心率。

现在，你想知道：练习瑜伽前后，学生们的心率是否有显著变化？

这时，你可以使用配对样本t检验来回答这个问题。这个检验会考虑每个学生在练习前和练习后的心率差异，然后计算这些差异的平均值，并确定这个平均值是否显著不同于零。

如果平均心率变化显著不同于零，那么就可以得出结论：练习瑜伽会对学生的心率产生显著影响。

这就是配对样本t检验的基本思想：通过比较同一组观察对象在两种不同条件下的观察结果来判断这两种条件是否有显著差异。

                   

单样本t检验

单样本t检验是一种用于检验一个样本的均值是否与已知的总体均值有显著差异的统计方法。

通俗地说，就是检验一个样本的平均值是否代表了整个总体的情况。

让我们通过一个简单的例子来解释单样本t检验：

假设你是一位生物学家，正在研究一种新的化肥对植物生长的影响。你想知道使用这种新化肥后，植物的平均生长是否与之前的平均生长有显著差异。

首先，你随机选择了一批植物作为样本，并测量了它们在使用新化肥后的生长情况。

然后，你将这些数据与之前已知的植物平均生长情况进行比较，看是否有显著差异。

这时，你可以使用单样本t检验来回答这个问题。这个检验会考虑你收集到的植物生长数据，然后将它们与已知的总体平均生长值进行比较。

如果你收集到的植物生长平均值与已知的总体平均值有显著差异，那么就可以得出结论：新化肥对植物生长有显著影响。

简而言之，单样本t检验就是通过比较一个样本的平均值与已知的总体平均值来判断样本是否代表了整个总体的情况。