树的基本概念
树(Tree)是一种重要的数据结构,它在计算机科学中被广泛应用于各种算法和程序中。树是由节点(node)组成的层次结构,其中每个节点都有一个父节点,除了根节点外,每个节点都有零个或多个子节点。树的一个关键特点是没有循环路径:从任何节点开始,通过父节点到达任何其他节点都是唯一的。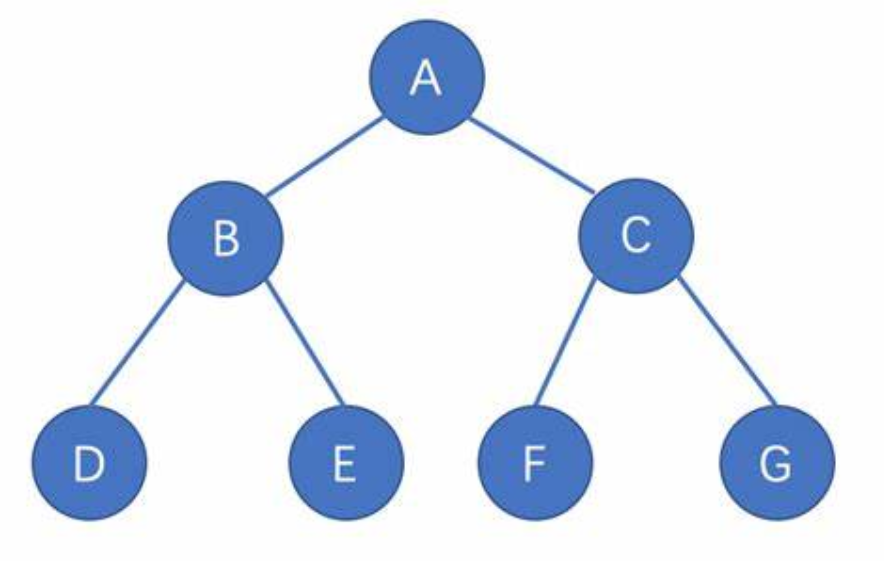
树的基本术语
节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I…等节点为叶节点
非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G…等节点为分支节点
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
森林:由m(m>0)棵互不相交的树的集合称为森林
常见类型的树
二叉树 (Binary Tree)
二叉搜索树(Binary Search Tree,BST)
平衡树(Balanced Tree)
树的表示
我们经常用孩子兄弟表示法进行树的结构表示
- 同层为兄弟关系
- 上下层为双亲与孩子的关系
表示法的代码构成:
typedef int Datatype;
struct Node
{
struct Node* first_Child; // 指向父亲对应的下一层的第一个孩子
struct Node* nextBrother; // 指向该层的下一个兄弟节点
// 每个节点存放的数据
}
图示: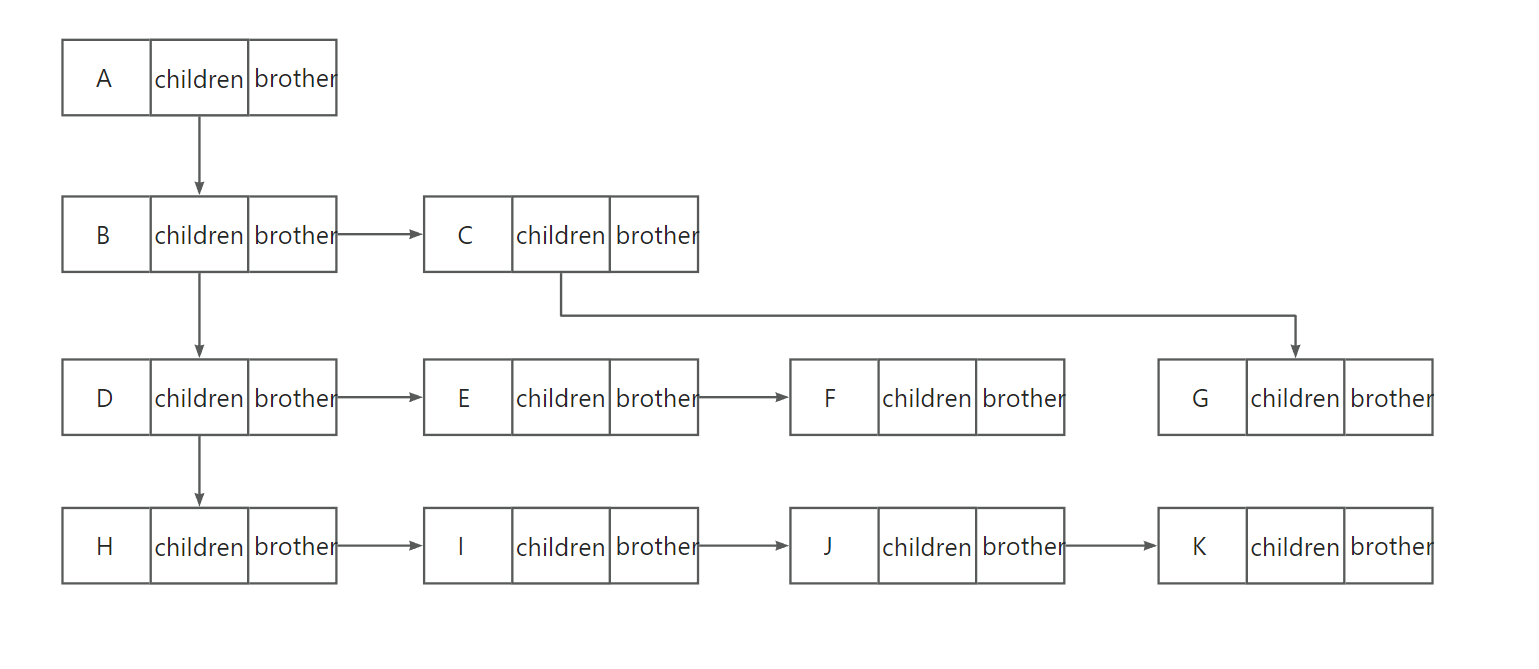
二叉树的概念和结构
二叉树(Binary Tree)是一种重要的数据结构,它由节点(node)组成的层次结构,每个节点最多有两个子节点,分别称为左子节点和右子节点。二叉树在计算机科学中被广泛应用,是许多其他数据结构和算法的基础。
二叉树的概念
根节点(Root):二叉树的顶部节点,它是整棵树的起点,没有父节点。
父节点(Parent):每个节点都有一个父节点,除了根节点外。父节点连接着它的子节点。
子节点(Child):每个节点最多有两个子节点,分别称为左子节点和右子节点。如果某个节点只有一个子节点或没有子节点,则相应的子节点为空。
叶子节点(Leaf):没有子节点的节点称为叶子节点。叶子节点位于树的底部,是树的末端。
二叉树的结构
1
/ \
2 3
/ \ / \
4 5 6 7
每个节点最多有两个子节点:每个节点最多有两个子节点,分别是左子节点和右子节点。
层次结构:二叉树是一种层次结构,每个节点的深度可以通过从根节点开始向下计算得到。
唯一路径:从根节点到任何其他节点都有唯一的路径,这保证了树的无环结构。
特殊的二叉树类型
- 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是
说,如果一个二叉树的层数为K,且结点总数是 ,则它就是满二叉树。
- 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K
的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对
应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
二叉树的存储结构
顺序存储
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空
间的浪费。而现实中使用中只有堆才会使用数组来存储,关于堆我们后面的章节会专门讲解。二叉树顺
序存储在物理上是一个数组,在逻辑上是一颗二叉树。
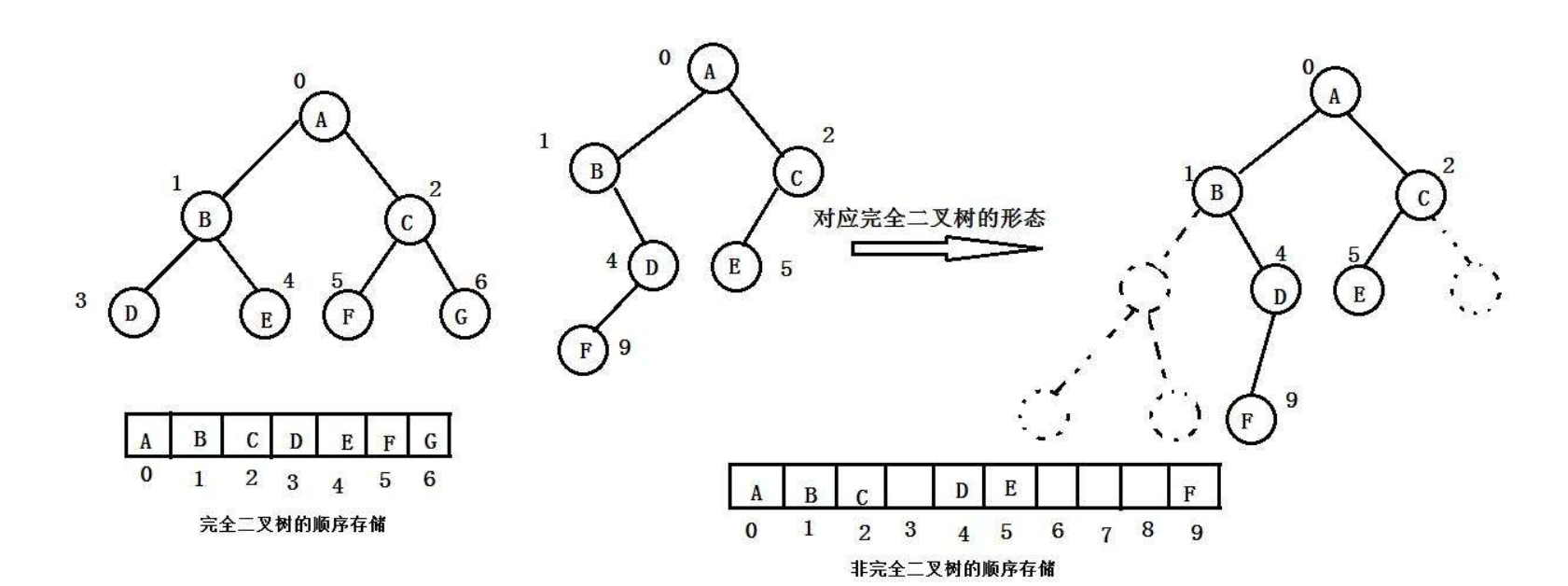
链式存储
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是
链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所
在的链结点的存储地址 。
链式存储示例代码:
#include <stdio.h>
#include <stdlib.h>
// 定义二叉树节点结构
typedef struct TreeNode
{
int data;
struct TreeNode* left;
struct TreeNode* right;
} TreeNode;
// 创建新节点
TreeNode* createNode(int value)
{
TreeNode* newNode = (TreeNode*)malloc(sizeof(TreeNode));
if (newNode == NULL)
{
printf("Memory allocation failed!\n");
exit(1);
}
newNode->data = value;
newNode->left = NULL;
newNode->right = NULL;
return newNode;
}
// 主函数
int main()
{
// 创建二叉树节点
TreeNode* root = createNode(1);
root->left = createNode(2);
root->right = createNode(3);
root->left->left = createNode(4);
root->left->right = createNode(5);
// 访问节点值并输出
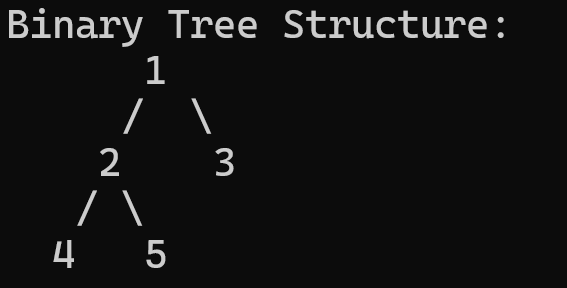
printf("Binary Tree Structure:\n");
printf(" %d\n", root->data);
printf(" / \\ \n");
printf(" %d %d\n", root->left->data, root->right->data);
printf(" / \\ \n");
printf(" %d %d\n", root->left->left->data, root->left->right->data);
return 0;
}
_感谢阅读_