1.时滞微分方程(DDE)的分类
时滞微分方程 (DDE) 是当前时间的解与过去时间的解相关的常微分方程。该时滞可以固定不变、与时间相关、与状态相关或与导数相关。要开始积分,通常必须提供历史解,以便求解器可以获取初始积分点之前的时间的解。
1.1常时滞 DDE
具有常时滞的微分方程组的形式如下:

DDE 的解通常是连续的,但其导数不连续。dde23
函数跟踪低阶导数的不连续性,并使用 ode23 使用的同一显式 Runge-Kutta (2,3) 对和插值求微分方程的积分。对于大于时滞的步长而言,Runge-Kutta 公式是隐式的。当 y(t) 足够平滑以证明此大小的步长时,使用预测-校正迭代法计算隐式公式。
1.2时间相关和状态相关的 DDE
常时滞 DDE 是一种特殊情况,更为一般的 DDE 形式为:

ddesd 函数用于求具有历史解 y(t) = S(t)(其中 t < t
0
)的时间相关和状态相关 DDE 的解 y(t)。
ddesd函数使用标准的四级、四阶显式 Runge-Kutta 法来求积分,并它控制自然插值的余值大小。它使用迭代来采用超过时滞的步长。
1.3 中立型 DDE
中立型的时滞微分方程涉及在 y ′ 以及 y 中的时滞:

2求解DDE的方法
2.1计算特定点的解
使用 deval
函数和任何 DDE 求解器的输出来计算积分区间中的特定点处的解。例如,
y = deval(sol,
0.5*(sol.x(1) + sol.x(end)))
计算积分区间中点处的解。
2.2历史解和初始值

2.3DDE 中的不连续性
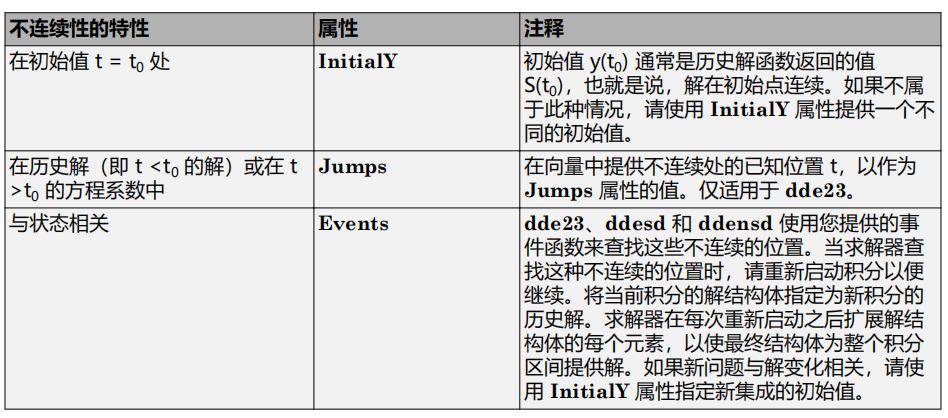
如果问题具有不连续性,最好使用 options 结构体将其传递给求解器。为此,请使用 ddeset 创建一个options
结构体以包含问题中的不连续性。
options 结构体中有三个属性可用于指定不连续性;
InitialY
、
Jumps
和
Events。选择的属性取决于不连续性的位置和特性。
3. 常时滞 DDE求解示例
以下示例说明如何使用 dde23
对具有常时滞的 DDE(时滞微分方程)方程组求解。
方程组为:

方程中的时滞仅存在于 y 项中,并且时滞本身是常量,因此各方程构成常时滞方程组。 要在 MATLAB® 中求解此方程组,您需要先编写方程组、时滞和历史解的代码,然后再调用时滞微分方程求解器
dde23,该求解器适用于具有常时滞的方程组。您可以将所需的函数作为局部函数包含在文件末尾(如本处所示),或者将它们作为单独的命名文件保存在 MATLAB 路径上的目录中。
3.1编写时滞代码
首先,创建一个向量来定义方程组中的时滞。此方程组有两种不同时滞:
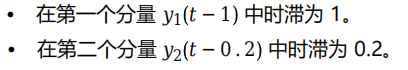
dde23
接受时滞的向量参数,其中每个元素是一个分量的常时滞。
lags = [1 0.2];3.2 编写方程代码
现在,创建一个函数来编写方程的代码。此函数应具有签名 dydt = ddefun(t,y,Z)
,其中:

function dydt = ddefun(t,y,Z)
ylag1 = Z(:,1);
ylag2 = Z(:,2);
dydt = [ylag1(1);
ylag1(1)+ylag2(2);
y(2)];
end3.3编写历史解代码
接下来,创建一个函数来定义历史解。历史解是时间 t
≤
t
0
的解。
function s = history(t)
s = ones(3,1);
end3.4求解方程
最后,定义积分区间 [t
0,
t
f ]
并使用
dde23
求解器对 DDE 求解。
tspan = [0 5];
sol = dde23(@ddefun, lags, @history, tspan);3.5对解进行绘图
解结构体 sol
具有字段
sol.x
和
sol.y,这两个字段包含求解器在这些时间点所用的内部时间步和对应的解。(如果您需要在特定点的解,可以使用
deval 来计算在特定点的解。)绘制三个解分量对时间的图。
plot(sol.x,sol.y,'-o')
xlabel('Time t');
ylabel('Solution y');
legend('y_1','y_2','y_3','Location','NorthWest');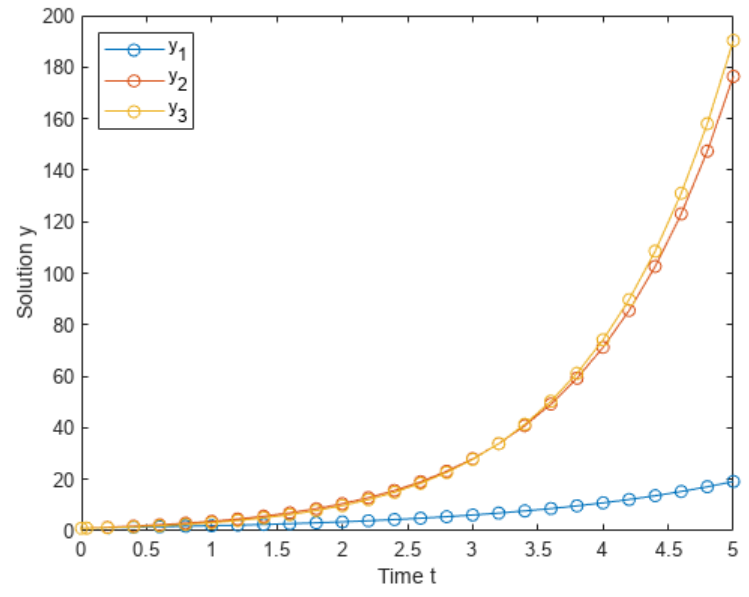
3.6 局部函数
此处列出了 DDE 求解器 dde23 为计算解而调用的局部辅助函数。您也可以将这些函数作为它们自己的文件保存在 MATLAB 路径上的目录中。
function dydt = ddefun(t,y,Z) % equation being solved
ylag1 = Z(:,1);
ylag2 = Z(:,2);
dydt = [ylag1(1);
ylag1(1)+ylag2(2);
y(2)];
end
%-------------------------------------------
function s = history(t) % history function for t <= 0
s = ones(3,1);
end