力扣题目链接
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking (vector<int>& nums, vector<bool>& used) {
// 此时说明找到了一组
if (path.size() == nums.size()) {
result.push_back(path);
return;
}
for (int i = 0; i < nums.size(); i++) {
// used[i - 1] == true,说明同一树枝nums[i - 1]使用过
// used[i - 1] == false,说明同一树层nums[i - 1]使用过
// 如果同一树层nums[i - 1]使用过则直接跳过
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
continue;
}
if (used[i] == false) {
used[i] = true;
path.push_back(nums[i]);
backtracking(nums, used);
path.pop_back();
used[i] = false;
}
}
}
public:
vector<vector<int>> permuteUnique(vector<int>& nums) {
result.clear();
path.clear();
sort(nums.begin(), nums.end()); // 排序
vector<bool> used(nums.size(), false);
backtracking(nums, used);
return result;
}
};
// 时间复杂度: 最差情况所有元素都是唯一的。复杂度和全排列1都是 O(n! * n) 对于 n 个元素一共有 n! 中排列方案。而对于每一个答案,我们需要 O(n) 去复制最终放到 result 数组
// 空间复杂度: O(n) 回溯树的深度取决于我们有多少个元素思路
这道题目和46.全排列 (opens new window)的区别在与给定一个可包含重复数字的序列,要返回所有不重复的全排列。
这里又涉及到去重了。
在40.组合总和II (opens new window)、90.子集II (opens new window)我们分别详细讲解了组合问题和子集问题如何去重。
那么排列问题其实也是一样的套路。
还要强调的是去重一定要对元素进行排序,这样我们才方便通过相邻的节点来判断是否重复使用了。
我以示例中的 [1,1,2]为例 (为了方便举例,已经排序)抽象为一棵树,去重过程如图:
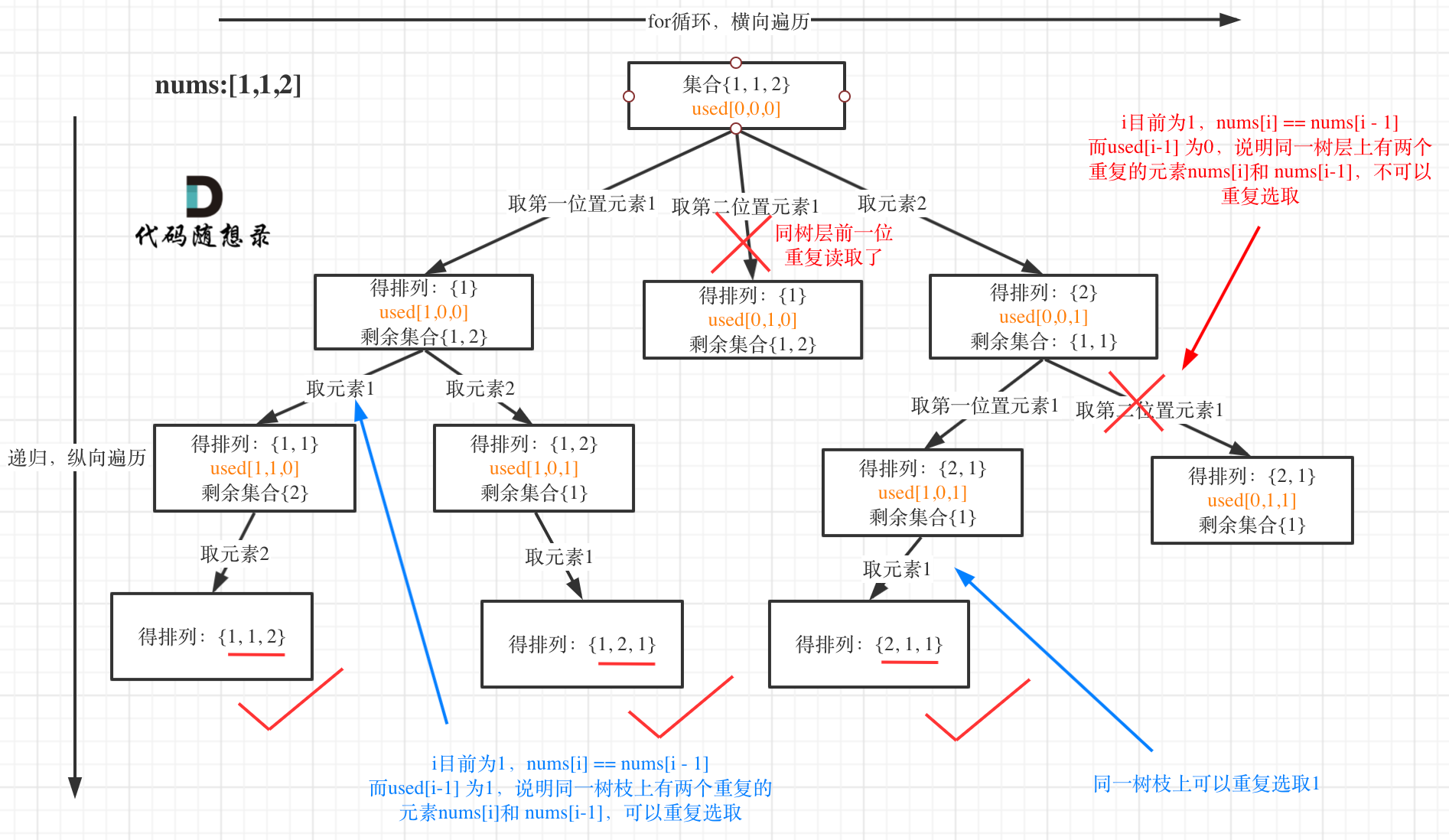
图中我们对同一树层,前一位(也就是nums[i-1])如果使用过,那么就进行去重。
一般来说:组合问题和排列问题是在树形结构的叶子节点上收集结果,而子集问题就是取树上所有节点的结果。
在46.全排列 (opens new window)中已经详细讲解了排列问题的写法,在40.组合总和II (opens new window)、90.子集II (opens new window)中详细讲解了去重的写法,所以这次我就不用回溯三部曲分析了
自己的思路:
重点是要理解去重的关键一步
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
continue;
}自己独立敲的代码先欠着呜呜呜,
因为还没能完全敲的出来~