一、什么是动态规划

通过拆分问题，定义问题状态和状态之间的关系，使得问题能够以递推的方式解决。

哪些问题可以使用动态规划？

1、具有最优子结构：问题的最优解所包含的子结构的解也是最优的

2、具有无后效性：未来与过去无关，只与当前状态有关。

二、三角形最小路径和

三、思路分析 

1、规整数据

将数组规整一下，将多余的空格删除，使之变成我们熟悉且好操作的常规形状。

[
    [2],
    [3, 4],
    [6, 5, 7],
    [4, 1, 8, 3]
]

变成这样后方便我们观察规律也比较好写算法，如果有题目要求输出题目中那样的，再添加空格字符串进行调整即可。

2、分析数据

2.1、只有两行数据

当只有两行数据时，只需要分别相加再求出最小值即可。

[
    [2],
    [3, 4]
]

2+3=5    2+4=6 ， 再取出相加和后的最小值，即为最小路径和。 

2.2、有三行数据

[
    [2],
    [3, 4],
    [6, 5, 7]
]

有三行数据时，路径选择就多了，一共有 4 种情况。

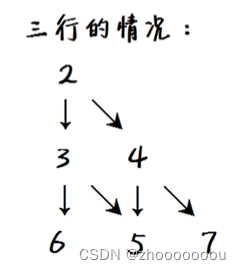
2 + 3 + 6 = 11      2 + 3 + 5 = 10   (前两项都是 2+3)

2 + 4 + 5 = 11      2 + 4 + 7 = 13   (前两项都是 2+4)

可以观察到，前两项的和我们在数据是两行的时候就已经计算过了，所以可以把他们保存到一个二维数组 dp[ i ][ j ] 中，后续直接使用数组中已经计算好的值，就不需要再遍历计算导致浪费时间了（如果数据很多的话）

tips：算完一行后把结果记录下来，用于下一行的计算。这个结果的物理意义就是从顶端到该点的最小路径和。

2.3、三类不同的节点

第一类：每行的第一个

每行的第一个形成的路径是直的，没有斜的，且每行第一个的坐标都是 [ i ][ 0 ]。

将当前节点的值更新为 上一行节点的和 加上 当前节点本来的值。

计算方式：

dp[ i ][ j ] : 新定义的二维数组，用于更新节点的和

triangle[ i ][ j ] ：原本的数组的值

dp[i][j] = dp[i-1][j] + triangle[i][j]

第二类：每行的最后一个

只能斜着往下走，上面没有值，且每一行最后一个的坐标 i == j

将当前节点的值更新为 上一行前一个的节点的和 加上 当前节点本来的值。

计算方式：

dp[i][j] = dp[i-1][j-1] + triangle[i][j]

第三类：每一行中间的

在更新中间的节点时，需要比较是 当前列上一行节点的和小 还是 前一列上一行的和小。

将较小值与当前值相加，得到输出：路径的最小和。

计算方式：

dp[i][j] = min(di[i-1][j], dp[i-1][j-1]) + triangle[i][j]

所有的都算完，所有可能的路径结果都在最后一行，对最后一行取最小值，即为正确结果 

3、代码实现

n = int(input())
triangle = [list(map(int, input().split())) for _ in range(n)]

dp = triangle[:]
for i in range(n):
    for j in range(i + 1):
        if j == 0:
            dp[i][j] = dp[i-1][j] + triangle[i][j]
        elif j == i:
            dp[i][j] = dp[i-1][j-1] + triangle[i][j]
        else:
            dp[i][j] = min(dp[i-1][j], dp[i-1][j-1]) + triangle[i][j]
print(min(dp[n-1]))

 

四、优化改进

将从上向下的顺序改为从下向上，这样看只有一类节点，不需要分三类节点进行分别考虑。

所有的情况都是两个节点取最小值后加上上一个节点。

从倒数第二行开始遍历，比较下一行的两个节点的大小，选最小值加上当前节点的值。

计算方式：

dp[i][j] = min(dp[i+1][j], dp[i+1][j+1]) + triangle[i][j]

改进代码实现：

n = int(input())
triangle = [list(map(int, input().split())) for _ in range(n)]

dp = triangle[:]
for i in range(n-2, -1, -1):
    for j in range(i+1):
        dp[i][j] = min(dp[i+1][j], dp[i+1][j+1]) + triangle[i][j]
print(dp[0][0])

可以看到，改进后的代码简洁清晰。