汉诺塔问题的递归算法解析

问题描述

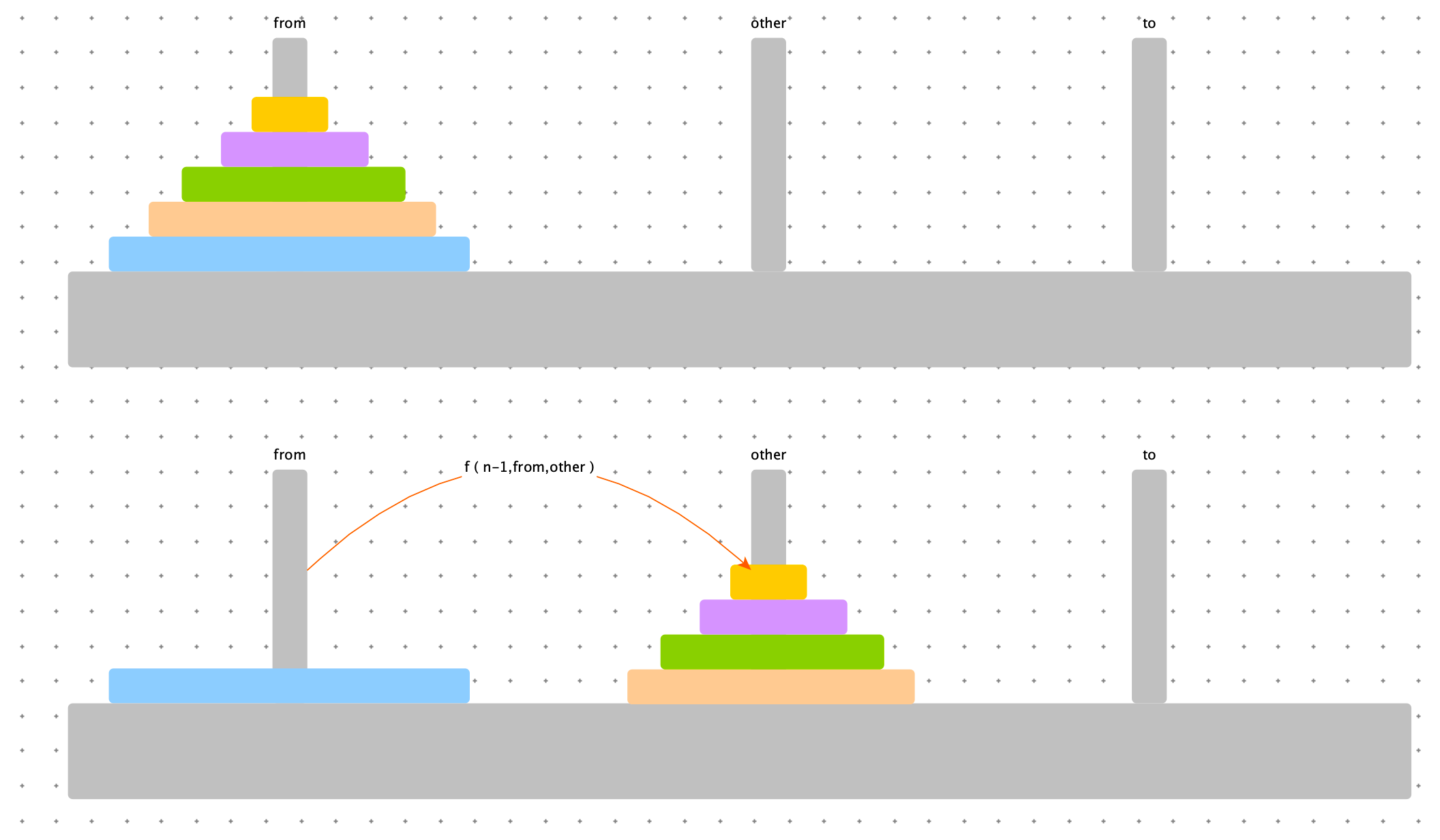
汉诺塔问题是一个经典的递归算法问题。问题描述如下：

在经典汉诺塔问题中，有 3 根柱子及 N 个不同大小的穿孔圆盘，盘子可以滑入任意一根柱子。一开始，所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。

请编写程序，用栈将所有盘子从第一根柱子移到最后一根柱子。

你需要原地修改栈。

示例1:
输入：A = [2, 1, 0], B = [], C = []
输出：C = [2, 1, 0]

示例2:
输入：A = [1, 0], B = [], C = []
输出：C = [1, 0]

提示:

• A中盘子的数目不大于14个。

递归算法思路

汉诺塔问题可以使用递归算法来解决。递归算法的核心思想是将问题分解为子问题，通过解决子问题来解决原问题。

对于汉诺塔问题，我们可以将其分解为以下三个步骤：

1. 将前 n-1 个盘子从源柱子移动到辅助柱子上。
2. 将第 n 个盘子从源柱子移动到目标柱子上。
3. 将前 n-1 个盘子从辅助柱子移动到目标柱子上。

递归的基础情况是当只有一个盘子时，直接将其从源柱子移动到目标柱子即可。

代码实现

以下是使用递归算法解决汉诺塔问题的代码实现：

class Solution {
public:
    void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {
        int n = A.size();
        move(n, A, B, C);
    }

    void move(int n, vector<int>& A, vector<int>& B, vector<int>& C) {
        if (n == 1) {
            C.push_back(A.back());
            A.pop_back();
            return;
        }
        
        move(n - 1, A, C, B);
        C.push_back(A.back());
        A.pop_back();
        move(n - 1, B, A, C);
    }
};

代码解释：

• 首先，我们定义了一个 hanota 函数，它接受三个栈作为参数，分别表示源柱子 A、辅助柱子 B 和目标柱子 C。
• 在 hanota 函数中，我们获取源柱子 A 中盘子的数量 n，然后调用 move 函数来进行递归移动。
• move 函数接受四个参数：盘子数量 n、源柱子 A、辅助柱子 B 和目标柱子 C。
• 在 move 函数中，我们首先判断基础情况，即当 n 等于 1 时，直接将源柱子 A 的顶部盘子移动到目标柱子 C，并返回。
• 如果 n 大于 1，我们递归地调用 move 函数，将前 n-1 个盘子从源柱子 A 移动到辅助柱子 B，然后将第 n 个盘子从源柱子 A 移动到目标柱子 C，最后再递归地调用 move 函数，将前 n-1 个盘子从辅助柱子 B 移动到目标柱子 C。

通过这样的递归调用，我们可以完成汉诺塔问题的移动过程。

算法复杂度分析

汉诺塔问题的递归算法的时间复杂度为 O(2^n)，其中 n 表示盘子的数量。这是因为对于 n 个盘子，我们需要进行 2^n-1 次移动操作。

空间复杂度为 O(n)，因为递归调用的深度为 n，每次递归调用都需要使用栈空间。

总结

汉诺塔问题是一个经典的递归算法问题，通过将问题分解为子问题，并使用递归的方式解决子问题，最终完成整个移动过程。递归算法的核心思想是将复杂问题分解为相似的子问题，通过解决子问题来解决原问题。

在实现递归算法时，需要注意以下几点：

1. 明确递归函数的定义和参数含义。
2. 确定递归的基础情况，即递归的终止条件。
3. 将问题分解为子问题，并递归地解决子问题。
4. 将子问题的解合并或组合，得到原问题的解。

递归算法虽然简洁易懂，但在某些情况下可能会导致递归调用的深度过大，从而引发栈溢出等问题。因此，在实际应用中，需要根据具体问题的特点选择合适的算法，并注意优化递归的效率。

通过学习汉诺塔问题的递归算法，我们可以加深对递归思想的理解，并掌握递归算法的设计和实现方法。这对于解决其他递归相关的问题具有重要的指导意义。