快速排序
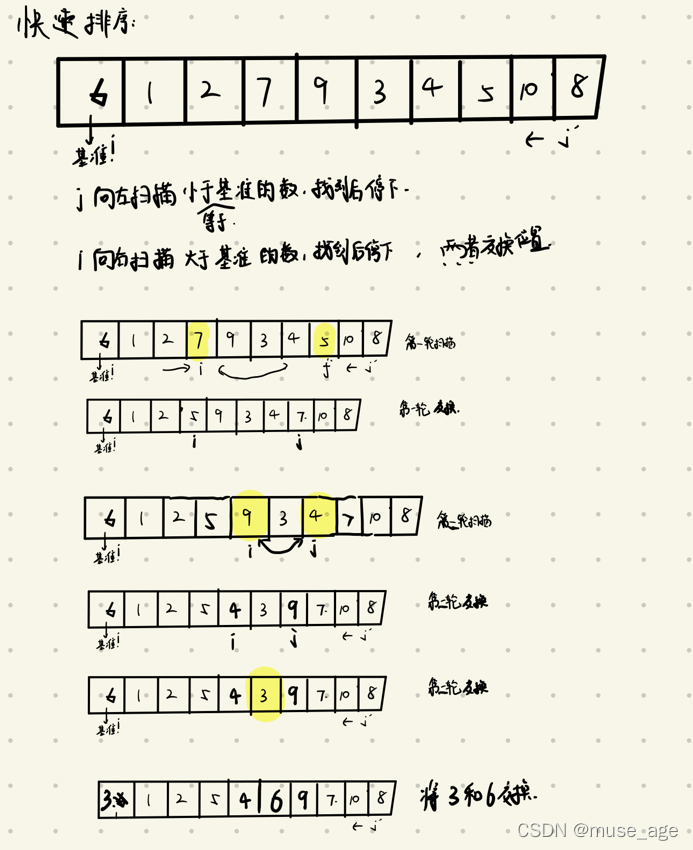
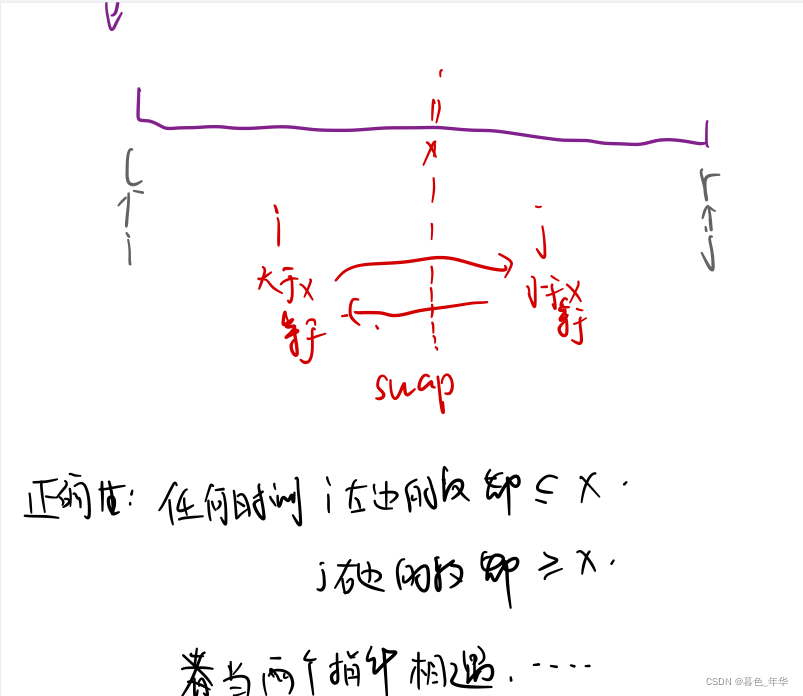
首先不妨以第一个数为基准数,在一轮遍历后,使基准数左边的数都小于基准数,基准数右边的数都大于基准数。
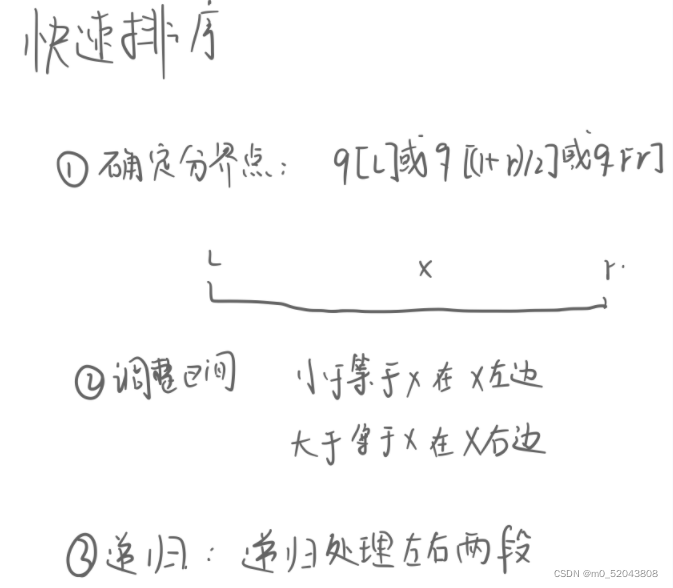
当然也可以取中间的数为基准数。
void quick_sort(vector<int>&nums,int l,int r){
if(l>=r)return;
int idx=l;//基准数选最左面
int i=l;
int j=r;
while(i<j){
while(i<j&&nums[j]>=nums[idx])j--;//右面先走
while(i<j&&nums[i]<=nums[idx])i++;
if(i<j){
int t=nums[i];
nums[i]=nums[j];
nums[j]=t;
}
}
int t=nums[idx];
nums[idx]=nums[i];
nums[i]=t;
quick_sort(nums,l,i-1);
quick_sort(nums,i+1,r);
}i,j相遇时,枢轴通常会被放置在两个指针相遇的位置上。
【排序算法】快速排序(C语言)_c语言快速排序-CSDN博客
霍尔法。(需要理解为什么,右面的先走。)
归并排序

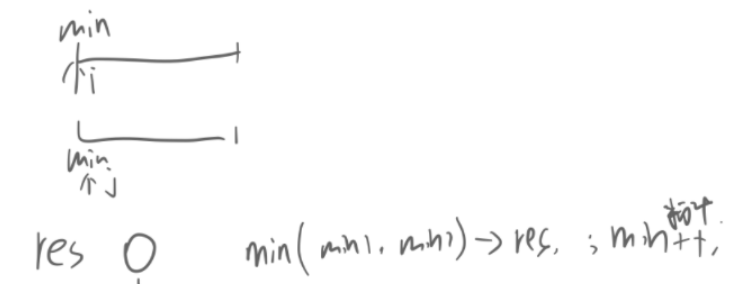
数组操作
void merge_sort(int q[],int l,int r){
if(l>=r)return;
int mid=(l+r)/2;
merge_sort(q,l,mid);
merge_sort(q,mid+1,r);
int k=0;
int i=l;
int j=mid+1;
while(i<=mid&&j<=r){
if(q[i]<=q[j])temp[k++]=q[i++];
else temp[k++]=q[j++];
}
while(i<=mid) temp[k++]=q[i++];
while(j<=r) temp[k++]=q[j++];
for(k=0,i=l;i<=r;) q[i++]=temp[k++];
}vector操作
vector<int> mergeSort(vector<int>&nums,int l,int r){
if(l==r)return {nums[l]};
int mid=(l+r)/2;
//递归排序左右区间
vector<int>left = mergeSort(nums,l,mid);
vector<int>right = mergeSort(nums,mid+1,r);
//双指针合并两个有序区间
vector<int>res; int n=left.size(); int m=right.size();
int i=0;
int j=0;
while(i<n&&j<m){
if(i<n&&j<m&&left[i]<right[j]){
res.push_back(left[i++]);
}else{
res.push_back(right[j++]);
}
}
while(i<n)res.push_back(left[i++]);
while(j<m)res.push_back(right[j++]);
return res;
}选择排序

void SelectSort(vector<int>&vec){
int min_k;
for(int i=0;i<vec.size();i++){
min_k=i;
for(int j=i;j<vec.size();j++){
if(vec[j]<vec[min_k])swap(j,min_k);
}
swap(vec[min_k],vec[i]);
}
}
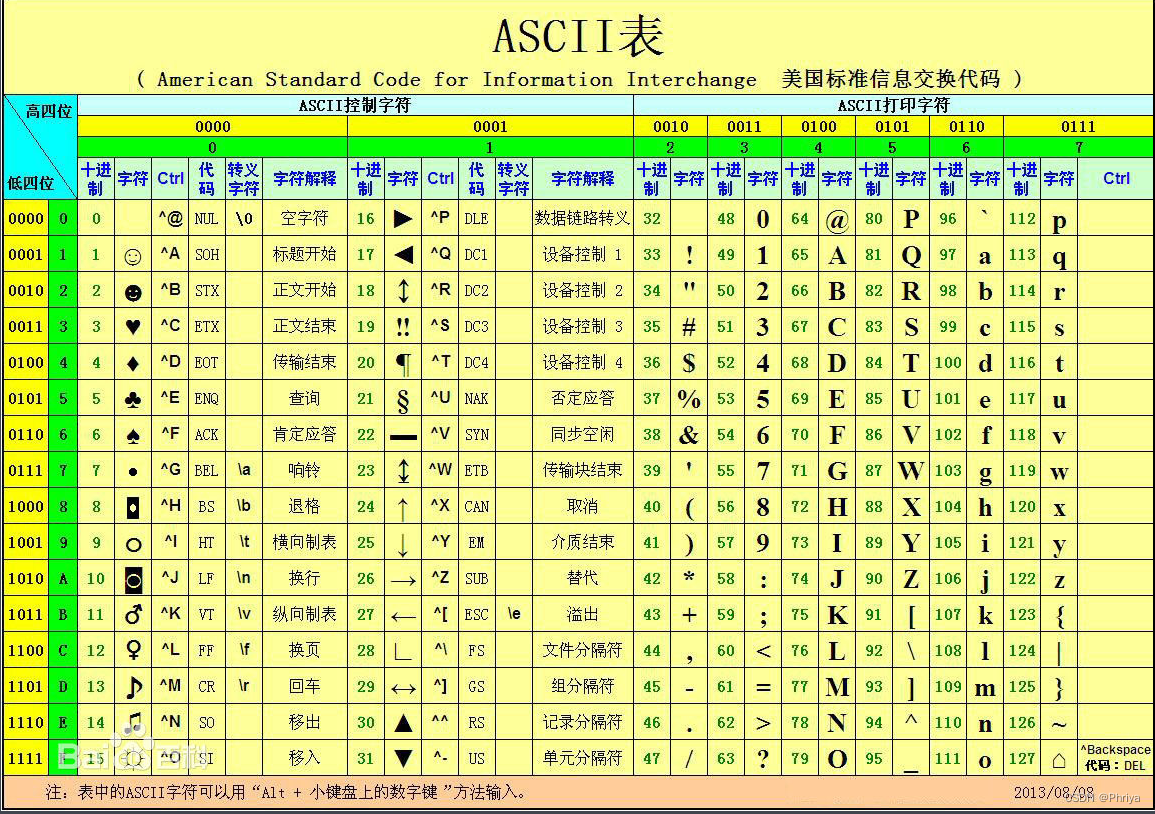
基数排序
基数排序:
通过将待排序元素按照位数进行分组,逐位地进行排序,从最低位到最高位,最终得到有序的结果。
基数排序的工作原理如下:
首先,找到待排序元素中的最大值,确定它的位数。从最低位(个位)开始,按照该位的值将元素进行分组(0到9),形成桶。依次从最低位到最高位,对每个桶中的元素按照分组顺序重新排列。重复上述过程,直到按照所有位数完成排序,得到最终有序的结果。
第一轮

第二轮

堆排序
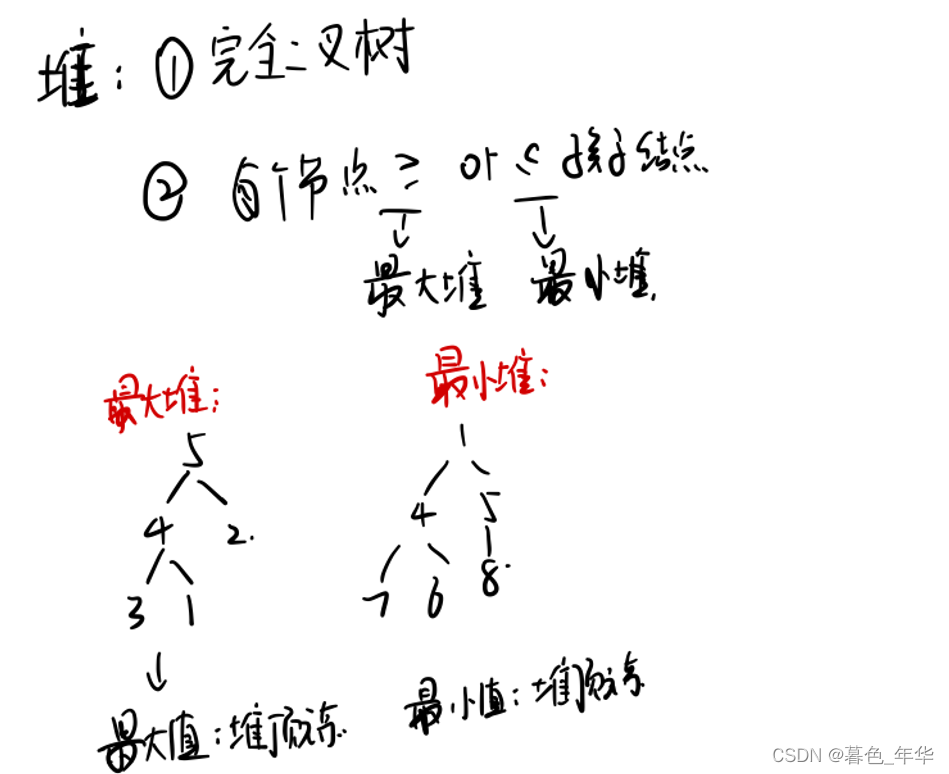
堆是一个完全二叉树,使用顺序存储结构。
(1是根节点,i的左孩子结点的下标为2*i,右孩子结点的下标为2*i+1)。
大根堆:每个结点的值都比左子树和右子树所有结点的值大。
小根堆:每个结点的值都比左子树和右子树所有结点的值小。
排序思想
1.将待排序的数组构造成一个大根堆,此时,整个数组的最大值就是堆结构的顶端
2.将顶端的数与末尾的数交换,此时,末尾的数为最大值,剩余待排序数组个数为n-1(进行删除根节点操作)
3.将剩余的n-1个数再构造成大根堆(只需进行一次down操作),再将顶端数与n-1位置的数交换,如此反复执行,便能得到有序数组。
堆的基本操作:调整:up(x); down(x);
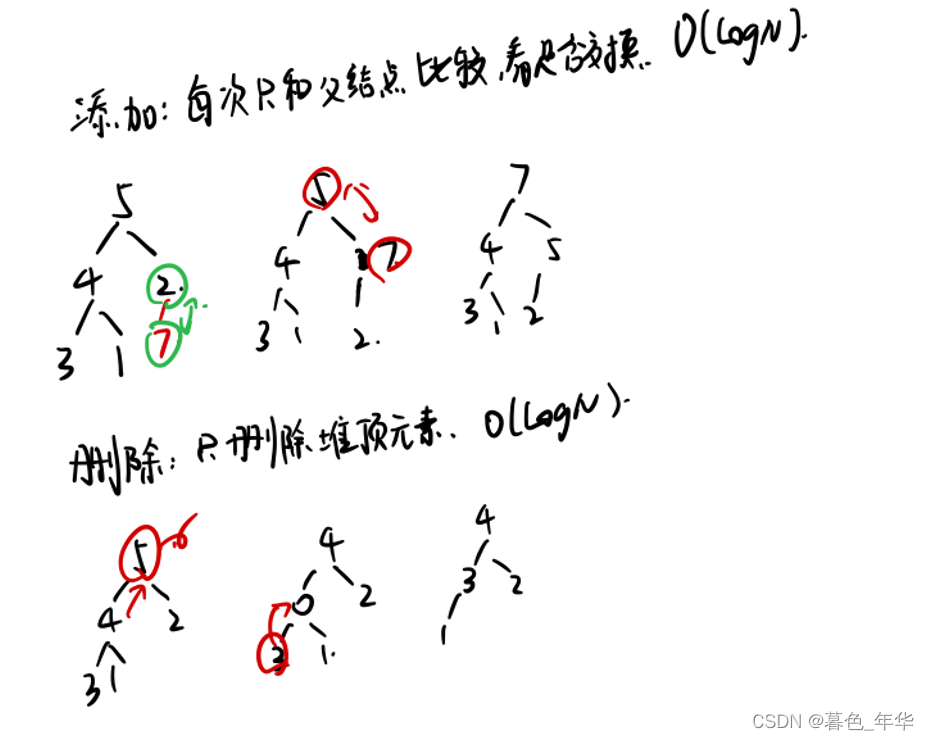
(1)插入一个数:heap[++size]=x;up(size);
把这个数放到完全二叉树的最后,然后对这个数进行up调整。
(2)求集合当中的最小值:heap[1];
(3)删除最小值:heap[1]=heap[size];size--;down(1);
用完全二叉树的最后一个数替换根节点,然后对根节点进行down调整。
(4)修改任意一个元素:heap[k]=x;down(k);up(k);
修改对应元素后,先进行down操作,再进行up操作。
down(x)操作(小根堆为例):(log(n))
比较x与其左右孩子结点的大小关系,如果比左右孩子大,就交换两个结点。
void down(int u){
int t=u;
if(u * 2<=size && h[u*2]<h[t]) t = u*2;
if(u * 2<=size && h[u*2+1]<h[t]) t = u*2+1;
// t表示u和左孩子和右孩子最小值的下标
// 如果u不是最小的,就交换x和t,并且递归对tdown操作
if(u!=t){
swap(h[u],h[t]);
down(t);
}
}



C++中堆的应用:
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
// 创建一个小根堆
priority_queue<int, vector<int>, greater<int>>minHeap;
// 创建一个大根堆
priority_queue<int>maxHeap;
//加元素
minHeap.push(10);
maxHeap.push(8);
//遍历堆
while (!minHeap.empty()) {
cout<<minHeap.top()<<" ";
minHeap.pop();
}
//取堆顶元素
minHeap.top();
maxHeap.top();
//删除并返回堆顶元素
minHeap.top();
minHeap.pop();