小朋友 A 在和 ta 的小伙伴们玩传信息游戏，游戏规则如下：

有 n 名玩家，所有玩家编号分别为 0 ～ n-1，其中小朋友 A 的编号为 0

每个玩家都有固定的若干个可传信息的其他玩家（也可能没有）。传信息的关系是单向的。每轮信息必须需要传递给另一个人，且信息可重复经过同一个人。

给定总玩家数 n，以及按 [玩家编号,对应可传递玩家编号] 关系组成的二维数组 relation。返回信息从小 A (编号 0 ) 经过 k 轮传递到编号为 n-1 的小伙伴处的方案数；若不能到达，返回 0。

示例 1：
输入：n = 5, relation = [[0,2],[2,1],[3,4],[2,3],[1,4],[2,0],[0,4]], k = 3
输出：3
解释：信息从小 A 编号 0 处开始，经 3 轮传递，到达编号 4。共有 3 种方案，分别是 0->2->0->4， 0->2->1->4， 0->2->3->4。

示例 2：
输入：n = 3, relation = [[0,2],[2,1]], k = 2
输出：0
解释：信息不能从小 A 处经过 2 轮传递到编号 2

限制：
2 <= n <= 10
1 <= k <= 5
1 <= relation.length <= 90, 且 relation[i].length == 2
0 <= relation[i][0],relation[i][1] < n 且 relation[i][0] != relation[i][1]

题目链接：https://leetcode.cn/problems/chuan-di-xin-xi/

参考题解链接：https://leetcode.cn/problems/chuan-di-xin-xi/solution/chuan-di-xin-xi-by-leetcode-solution/

可以通过深度优先搜索、广度优先搜索或动态规划实现

1. • 深度优先搜索

从节点 0 出发做深度优先搜索，每一步记录当前所在的节点以及经过的轮数，当经过 k 轮时，如果位于节点 n-1，则将方案数加 1。搜索结束后可得到总的方案数。

class Solution:
    def numWays(self, n: int, relation: List[List[int]], k: int) -> int:
        # 将 某节点-该节点能到达的节点列表 存成字典
        edges = collections.defaultdict(list)
        for src, dst in relation:
            edges[src].append(dst)
        
        ways = 0
        #深度优先搜索方法，参数 到达的节点node，经过了多少步 steps
        def dfs(node, steps):
            #如果步数为k，判断所在节点是否为n-1，是则所求路径数加一
            if steps == k:
                if node == n - 1:
                    nonlocal ways
                    ways += 1
                return
            for nextNode in edges[node]:
                dfs(nextNode,steps+1)

        #从节点 0 出发做深度优先搜索      
        dfs(0,0)
        return ways 

上述深度优先搜索作为内部函数，也可以拿出来作为一个方法，如下，

class Solution:
    def numWays(self, n: int, relation: List[List[int]], k: int) -> int:
        self.ways , self.n, self.k = 0, n, k
        # 将 某节点-该节点能到达的节点列表 存成字典
        self.edges = collections.defaultdict(list)
        for src, dst in relation:
            self.edges[src].append(dst)

        #从节点 0 出发做深度优先搜索
        self.dfs(0,0)
        return self.ways 

    #深度优先搜索方法，参数 到达的节点node，经过了多少步 steps
    def dfs(self, node, steps):
        #如果步数为k，判断所在节点是否为n-1，是则所求路径数加一
        if steps == self.k:
            if node == self.n - 1:
                self.ways += 1
            return
        for nextNode in self.edges[node]:
            self.dfs(nextNode,steps+1)

2. 广度优先搜索

从节点 0 出发做广度优先搜索，当遍历到 k层时，如果位于节点 n-1，则将方案数加 1。

class Solution:
    def numWays(self, n: int, relation: List[List[int]], k: int) -> int:
        # 将 某节点-该节点能到达的节点列表 存成字典
        edges = collections.defaultdict(list)
        for src, dst in relation:
            edges[src].append(dst)
        steps = 0
        ways = 0
        # 初始化一个队列，该队列里只有初始节点0
        queue = collections.deque([0])

        # 当走的步数小于k时/遍历的层数小于k时，把每层的节点逐个拎出来，再用一层循环找到每个节点的所有可能的下一个节点，append到队列，做完这个操作相当于往前走了一步（层），steps 加一
        while queue and steps < k:
            for i in range(len(queue)):
                node = queue.popleft()

                for nextNode in edges[node]:
                    queue.append(nextNode)
                
            steps += 1
        #遍历到第k层，即走了k步，不满足上述循环条件，此时steps为 k，queue中是第k层的目标节点，即全部路径走到第k步所在的节点
        if steps == k:
            for node in queue:
                #如果此时所在的节点是n-1，所求路径数加一
                if node == n-1:
                    ways += 1
        return ways
            

3. 动态规划

定义动态规划的状态 dp[i][j] 为经过 i 轮传递到节点 j 的方案数，其中 0<=i<=k，0<=j<=n-1。

如果第 i 轮传递到编号 src 的玩家，则第 i+1 轮可以从编号 src 的玩家传递到编号 dst 的玩家。

动态规划的状态转移方程：

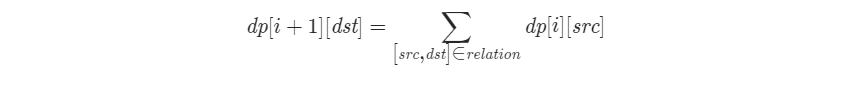
class Solution:
    def numWays(self, n: int, relation: List[List[int]], k: int) -> int:
        #初始化一个k+1行，n列的二维数组
        dp = [[0] * n for _ in range(k + 1)]

        #当 i=0时，一定位于编号 0的玩家，j!=0 时，dp[0][j] = 0 ，保持初始化的0即可
        dp[0][0] = 1
        for i in range(k):
            for src,dst in relation:
                dp[i + 1][dst] += dp[i][src]
        # 返回经过 k 轮传递到节点 n-1 的方案数
        return dp[k][n - 1]