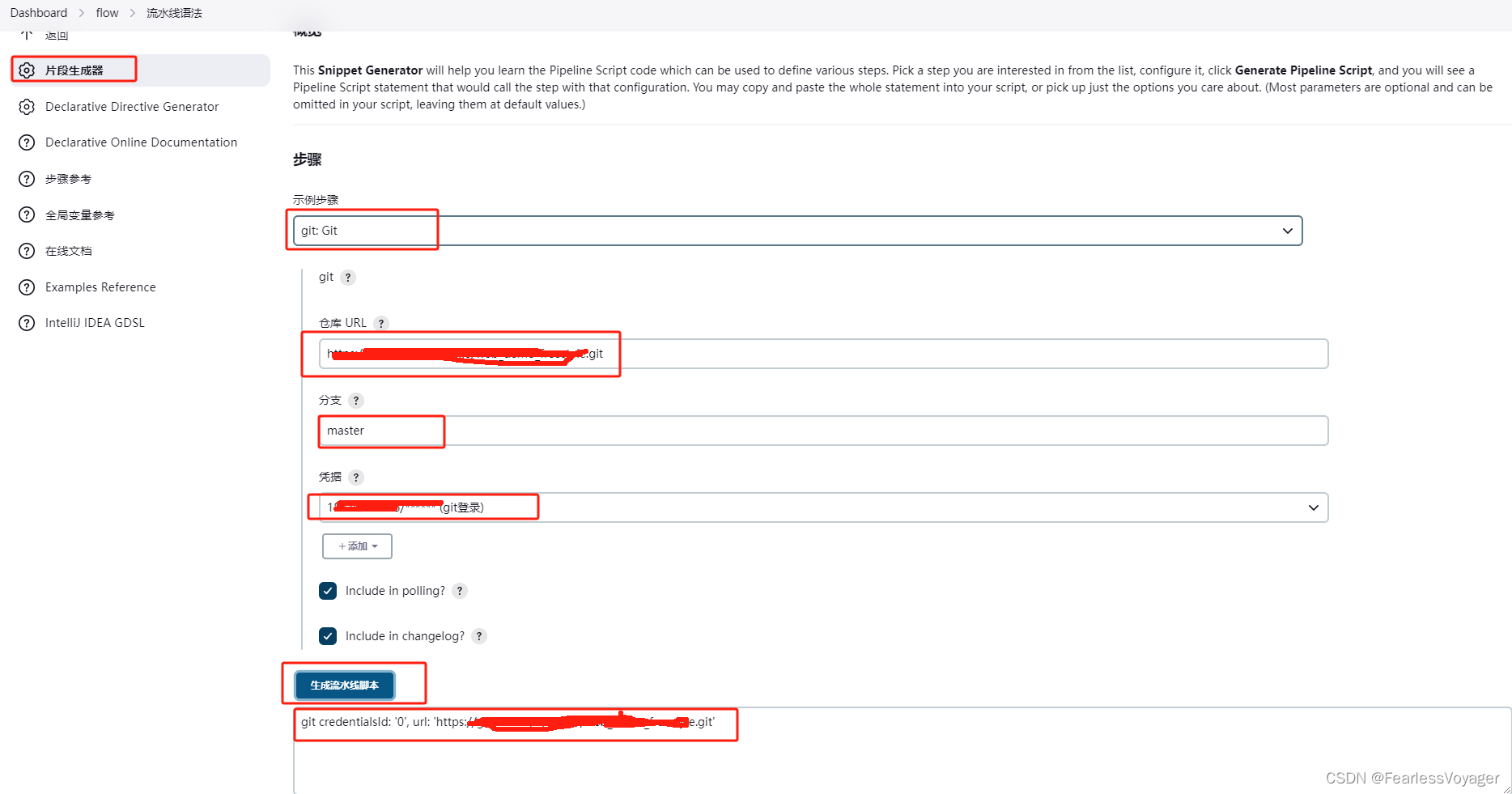
边的类型

neighbors(邻居)：两个顶点有一条共同边

loop：链接自身

link：两个顶点有一条边

parallel edges：两个顶点有两条及以上条边

无向图

必要条件：删掉顶点数一定大于等于剩下的顶点数

设无向图G=<V,E>是哈密顿图，S是V的任意的非空真子集， ==w(G-S)≤|S| ==其中，w(G-S)为从G中删除S(删除S中各顶点及关联的边)后所得到的图的连通分支数。

设无向图G=<V,E>是半哈密顿图，则对于结点集V的任意非空真子集S均有w(G-S)≤|S| +1。

每个度数要大于边数的一半

哈密尔顿图加环后仍是哈密尔顿图

如果简单图的顶点数大于3，并为完全图，则是哈密尔顿图

有向图Directed Graphs

竞赛图是个强连通图，一定是哈密尔顿图

竞赛图一定是半哈密尔顿图，且加上一点可以变成哈密尔顿图。

底图

有向图将方向去掉后得到的无向图

简单有向图的底图不一定是简单图

简单有向图

1.不可以有环

2.不允许平行

图的类型

finite：有限的顶点和边

trivial：只有一个顶点

simple：只有link

完全图complete graph

是个简单图，任意两个顶点相连A simple graph in which each pair of distinct vertices are adjacent is a complete graph.

特点：

1.有n个顶点的完全图，则有n(n—1)/2条边

We denote the complete graph on n vertices by Kn; K4 and K5 are shown in Fig. 3.2. You should check that Kn has n(n—1)/2 edges.

二部图bipartite

把顶点分成两部分，边只在两部分之间，判断：如果产生奇数环就不可能是二部图，表达：G(X,Y)，所有环都有偶数条边，一定是二部图，反之亦然。

欧拉图Eulerian graphs

概述：一笔画问题

通过图中所有边恰好一次且行遍所有顶点的回路称为欧拉回路。具有欧拉回路的无向图称为欧拉图。An Euler trail is a path in a graph that visits every edge exactly once. In other words, it is a path that starts from one vertex and ends at another vertex, and it traverses every edge of the graph exactly once.

有Euler trail的无向图的特点:

1. The graph must be connected.
2. The graph must have at most two vertices with odd degree.偶数点，每个点都有偶数个度

有Euler trail的有向图的特点:

1. 入度等于出度

If a graph has exactly two vertices with odd degree, then an Euler trail must start at one of those vertices and end at the other. If a graph has no vertices with odd degree, then it has an Euler circuit, which is an Euler trail that starts and ends at the same vertex.

把小环走一遍后删去，直到没有边了，最后按反顺序拼起来就是欧拉图的走向，

强连通图不一定是欧拉图，但欧拉图一定是强连通图

每个点出度等于入度

fleury‘s algorithm：用来寻找欧拉回路

1. 确保图形有0个或2个奇数顶点。
2. 如果有0个奇数顶点，则从任意位置开始。如果有两个奇数顶点，请从其中一个开始。
3. 沿边一次一条。如果要在桥和非桥之间进行选择，请始终选择非桥。
4. 边缘用完时停止。

半欧拉图semi-Eulerian

通过图中所有边恰好一次且行遍所有顶点的通路称为欧拉通路。具有欧拉通路但不具有欧拉回路的无向图称为半欧拉图。

如果一个无向图有恰好两个奇数点（度为奇数），那么它就是一个半欧拉图。半欧拉图有欧拉通路，但没有欧拉回路。

判断欧拉图和半欧拉图

无向图G为欧拉图当且仅当G连通且无奇度顶点. G是半欧拉图当且仅当G连通且恰有两个奇度顶点.

有向图D是欧拉图当且仅当D连通且每个顶点的入度都等于出度. D是半欧拉图当且仅当D连通且恰有两个奇度顶点, 其中一个入度比出度大1, 另一个出度比入度大1, 其余顶点的入度等于出度.

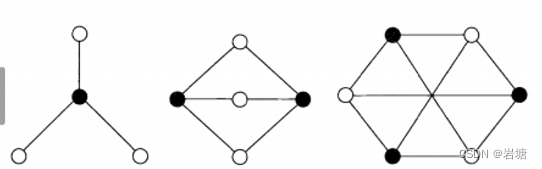
柏拉图图​​​​​​​Platonic graphs

柏拉图图由五个正(柏拉图)体——四面体、八面体、立方体、二十面体和十二面体的顶点和边构成。

Platonic graphs are formed from the vertices and edges of the five regular (Platonic) solids - the tetrahedron, octahedron, cube, icosahedron and dodecahedron.

Hamiltonian哈密尔顿图

每个顶点访问一次，并能回到顶点

哈密顿路：给定无向图G中，通过图中每个结点一次而且仅一次的路径。

哈密顿回路：给定无向图G中，通过图中每个结点一次而且仅一次的回路。

哈密顿图：具有哈密顿回路的图。

半哈密顿图：有哈密顿路径而没有哈密顿回路的图。哈密尔顿图和半哈密尔顿图是连通图。 哈密顿图和欧拉图联系：两者都是遍历问题，但是欧拉图考虑的是边，而哈密顿考虑的是结点。同时判定欧拉图具有充要条件。但是哈密顿图没有简单的充要条件，只有必要条件和充分条件。

迪克斯特拉算法

步骤：

1. 找到“最便宜”的节点（可在最短时间内到达的节点）。
2. 更新该节点的邻居节点的开销。
3. 重复这个过程，直到对图中每个节点都做了。
4. 计算最终路径。