题目所属分类

flod最短路算法

原题链接

给你一个变量对数组 equations 和一个实数值数组 values 作为已知条件，其中 equations[i] = [Ai, Bi] 和 values[i] 共同表示等式 Ai / Bi = values[i] 。每个 Ai 或 Bi 是一个表示单个变量的字符串。

另有一些以数组 queries 表示的问题，其中 queries[j] = [Cj, Dj] 表示第 j 个问题，请你根据已知条件找出 Cj / Dj = ? 的结果作为答案。

返回所有问题的答案。如果存在某个无法确定的答案，则用 -1.0 替代这个答案。如果问题中出现了给定的已知条件中没有出现的字符串，也需要用 -1.0 替代这个答案。

注意：输入总是有效的。你可以假设除法运算中不会出现除数为 0 的情况，且不存在任何矛盾的结果。

代码案例：
输入：equations = [[“a”,“b”],[“b”,“c”]], values = [2.0,3.0], queries = [[“a”,“c”],[“b”,“a”],[“a”,“e”],[“a”,“a”],[“x”,“x”]]
输出：[6.00000,0.50000,-1.00000,1.00000,-1.00000]
解释：
条件：a / b = 2.0, b / c = 3.0
问题：a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ?
结果：[6.0, 0.5, -1.0, 1.0, -1.0 ]

题解

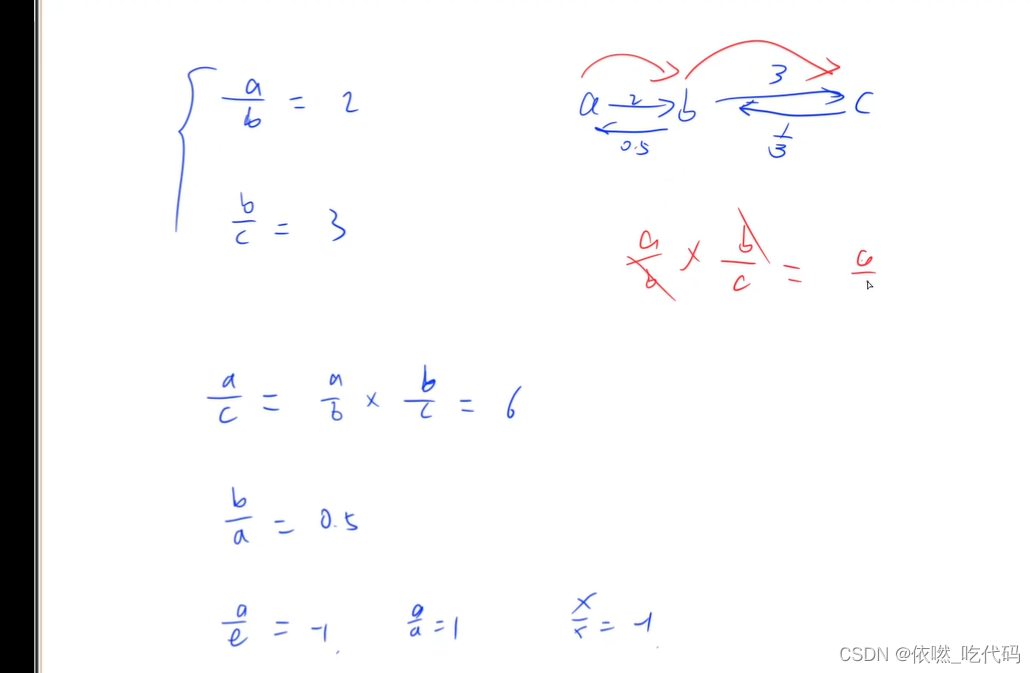
在这里插入图片描述
可以转换成图论的问题

class Solution {
    public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {
         // 存储带权有向边
        Map<String,Map<String,Double>> dist = new HashMap<>();
        // 存储所有顶点
        Set<String> vs = new HashSet<>();
         // 遍历所有的方程，将顶点存入 vers，边存入 dist
         for(int i = 0 ; i < equations.size() ; i++){
             List<String> e = equations.get(i) ;
             String a = e.get(0);
             String b = e.get(1);
            double  v = values[i] ;
             vs.add(a);
             vs.add(b);
             dist.computeIfAbsent(a , l -> new HashMap<>()).put(b,v);
             dist.computeIfAbsent(b , l -> new HashMap<>()).put(a,1 / v);
         }
         // floyd 求多源最短路，因为路径是唯一的，所以相当于就是求两点之间的距离
        // floyd 先确定中间节点，而后遍历首尾两个节点
            for(String k :vs){
                for(String i : vs){
                    for(String j : vs){
                        if(dist.get(i).containsKey(k) && dist.get(k).containsKey(j)){
                            double d = dist.get(i).get(k) * dist.get(k).get(j);
                             dist.get(i).put(j , d);
                        }                                             
                    }
                }
            }

            //查询所有
            double[] res = new double[queries.size()];
            for(int i = 0 ;  i < queries.size() ; i++){
                String a = queries.get(i).get(0);
                String b = queries.get(i).get(1);
                if(dist.containsKey(a) && dist.get(a).containsKey(b))res[i] = dist.get(a).get(b);
                else res[i] = -1.0 ;
            }
            return res ;
         
    }
}

y总的C++写法 Java写的话很费事

class Solution {
public:
    vector<double> calcEquation(vector<vector<string>>& equations, vector<double>& values, vector<vector<string>>& queries) {
        unordered_set<string> vers;
        unordered_map<string, unordered_map<string, double>> d;
        for (int i = 0; i < equations.size(); i ++ ) {
            auto a = equations[i][0], b = equations[i][1];
            auto c = values[i];
            d[a][b] = c, d[b][a] = 1 / c;
            vers.insert(a), vers.insert(b);
        }

        for (auto k: vers)
            for (auto i: vers)
                for (auto j: vers)
                    if (d[i][k] && d[j][k])
                        d[i][j] = d[i][k] * d[k][j];

        vector<double> res;
        for (auto q: queries) {
            auto a = q[0], b = q[1];
            if (d[a][b]) res.push_back(d[a][b]);
            else res.push_back(-1);
        }

        return res;
    }
};

作者：yxc
链接：https://www.acwing.com/activity/content/code/content/524881/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。