图像最近邻插值、双线性插值和双三次插值
用 O ( X , Y ) O(X,Y) O(X,Y)表示 H × W H\times W H×W的原始图像, G ( X ^ , Y ^ ) G(\hat{X},\hat{Y}) G(X^,Y^)表示 H ^ × Y ^ \hat{H}\times\hat{Y} H^×Y^的目标图像。
最近邻插值
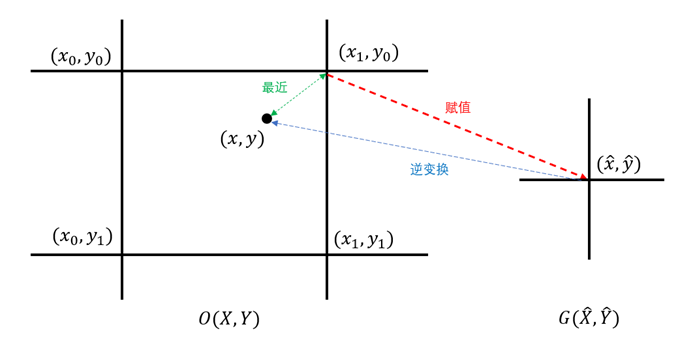
最近邻插值法令目标图像在 ( x ^ , y ^ ) (\hat{x},\hat{y}) (x^,y^)的像素值 G ( x ^ , y ^ ) G(\hat{x},\hat{y}) G(x^,y^)等于逆变换到原始图像后 ( x , y ) (x,y) (x,y) 距离其最近的点的像素值。用公式表示为:
G ( x ^ , y ^ ) = O ( round ( x ^ ⋅ W W ^ ) , round ( y ^ ⋅ H H ^ ) ) G(\hat{x}, \hat{y})=O\left(\operatorname{round}\left(\frac{\hat{x} \cdot W}{\hat{W}}\right), \operatorname{round}\left(\frac{\hat{y} \cdot H}{\hat{H}}\right)\right) G(x^,y^)=O(round(W^x^⋅W),round(H^y^⋅H))
其中 x ^ ⋅ W W ^ \frac{\hat{x}\cdot W}{\hat{W}} W^x^⋅W和 y ^ ⋅ H H ^ \frac{\hat{y}\cdot H}{\hat{H}} H^y^⋅H为逆变换; r o u n d ( ) round() round()表示四舍五入,用于得到源图像中的最近点坐标。
双线性插值
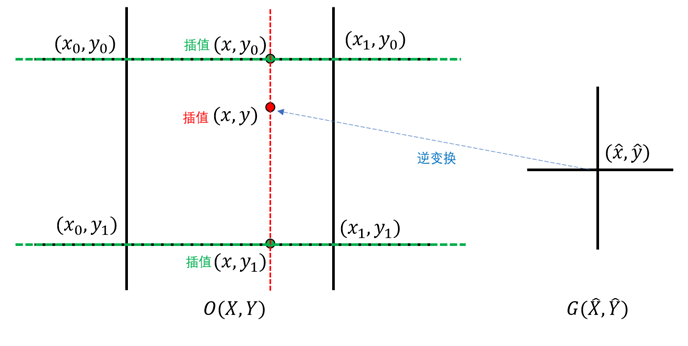
双线性插值使用的逆变换为(需要考虑对齐):
x = x ^ ( W / W ^ ) + 0.5 ( W / W ^ − 1 ) y = y ^ ( H / H ^ ) + 0.5 ( H / H ^ − 1 ) \begin{array}{l} x=\hat{x}(W / \hat{W})+0.5(W / \hat{W}-1) \\ y=\hat{y}(H / \hat{H})+0.5(H / \hat{H}-1) \end{array} x=x^(W/W^)+0.5(W/W^−1)y=y^(H/H^)+0.5(H/H^−1)
双线性插值是在
X
X
X上进行两次线性插值计算,然后在
Y
Y
Y方向上进行一次插值计算。首先在
X
X
X方向上进行两次线性插值,得到:
O
(
x
,
y
0
)
=
x
1
−
x
x
1
−
x
0
O
(
x
0
,
y
0
)
+
x
−
x
0
x
1
−
x
0
O
(
x
1
,
y
0
)
O
(
x
,
y
1
)
=
x
1
−
x
x
1
−
x
0
O
(
x
0
,
y
1
)
+
x
−
x
0
x
1
−
x
0
O
(
x
1
,
y
1
)
\begin{array}{l} O\left(x, y_{0}\right)=\frac{x_{1}-x}{x_{1}-x_{0}} {O}\left(x_{0}, y_{0}\right)+\frac{x-x_{0}}{x_{1}-x_{0}} {O}\left(x_{1}, y_{0}\right) \\ O\left(x, y_{1}\right)=\frac{x_{1}-x}{x_{1}-x_{0}} {O}\left(x_{0}, y_{1}\right)+\frac{x-x_{0}}{x_{1}-x_{0}} O\left(x_{1}, y_{1}\right) \end{array}
O(x,y0)=x1−x0x1−xO(x0,y0)+x1−x0x−x0O(x1,y0)O(x,y1)=x1−x0x1−xO(x0,y1)+x1−x0x−x0O(x1,y1)
然后在
Y
Y
Y方向上进行一次线性插值,得到:
O
(
x
,
y
)
=
y
1
−
y
y
1
−
y
0
O
(
x
,
y
0
)
+
y
−
y
0
y
1
−
y
0
O
(
x
,
y
1
)
O(x, y)=\frac{y_{1}-y}{y_{1}-y_{0}} O\left(x, y_{0}\right)+\frac{y-y_{0}}{y_{1}-y_{0}} O\left(x, y_{1}\right)
O(x,y)=y1−y0y1−yO(x,y0)+y1−y0y−y0O(x,y1)
综合起来,就是双线性插值的结果
G
(
x
^
,
y
^
)
=
(
y
1
−
y
)
(
x
1
−
x
)
(
y
1
−
y
0
)
(
x
1
−
x
0
)
O
(
x
0
,
y
0
)
+
(
y
1
−
y
)
(
x
−
x
0
)
(
y
1
−
y
0
)
(
x
1
−
x
0
)
O
(
x
1
,
y
0
)
+
(
y
−
y
0
)
(
x
1
−
x
)
(
y
1
−
y
0
)
(
x
1
−
x
0
)
O
(
x
0
,
y
1
)
+
(
y
−
y
0
)
(
x
−
x
0
)
(
y
1
−
y
0
)
(
x
1
−
x
0
)
O
(
x
1
,
y
1
)
\begin{aligned} G(\hat{x}, \hat{y})= & \frac{\left(y_{1}-y\right)\left(x_{1}-x\right)}{\left(y_{1}-y_{0}\right)\left(x_{1}-x_{0}\right)} {O}\left(x_{0}, y_{0}\right) \\ & +\frac{\left(y_{1}-y\right)\left(x-x_{0}\right)}{\left(y_{1}-y_{0}\right)\left(x_{1}-x_{0}\right)} O\left(x_{1}, y_{0}\right) \\ & +\frac{\left(y-y_{0}\right)\left(x_{1}-x\right)}{\left(y_{1}-y_{0}\right)\left(x_{1}-x_{0}\right)} O\left(x_{0}, y_{1}\right) \\ & +\frac{\left(y-y_{0}\right)\left(x-x_{0}\right)}{\left(y_{1}-y_{0}\right)\left(x_{1}-x_{0}\right)} O\left(x_{1}, y_{1}\right) \end{aligned}
G(x^,y^)=(y1−y0)(x1−x0)(y1−y)(x1−x)O(x0,y0)+(y1−y0)(x1−x0)(y1−y)(x−x0)O(x1,y0)+(y1−y0)(x1−x0)(y−y0)(x1−x)O(x0,y1)+(y1−y0)(x1−x0)(y−y0)(x−x0)O(x1,y1)
双三次插值
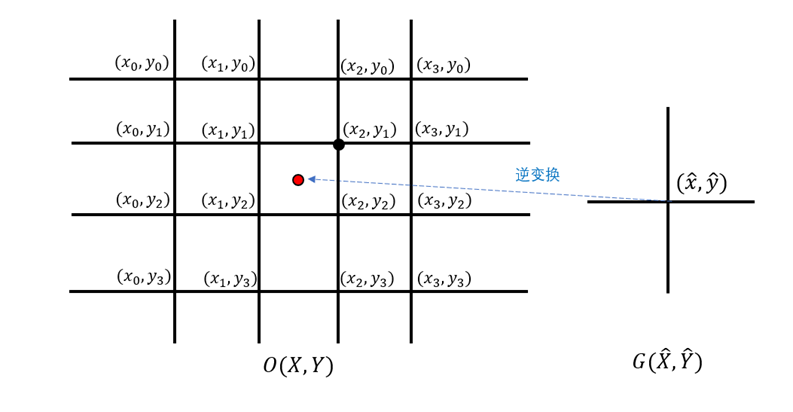
如图3所示,双三次插值通过对周边16个点进行加权计算得到目标像素点的值,加权系数常采用基于BiCubic基函数的方法,该函数形式如下:
W ( d ) = { ( a + 2 ) ∣ d ∣ 3 − ( a + 3 ) ∣ d ∣ 2 + 1 for ∣ d ∣ ≤ 1 a ∣ d ∣ 3 − 5 a ∣ d ∣ 2 + 8 a ∣ d ∣ − 4 a for 1 < ∣ d ∣ < 2 0 otherwise W(d)=\left\{\begin{array}{cc} (a+2)|d|^{3}-(a+3)|d|^{2}+1 & \text { for }|d| \leq 1 \\ a|d|^{3}-5 a|d|^{2}+8a|d|-4 a & \text { for } 1<|d|<2 \\ 0 & \text { otherwise } \end{array}\right. W(d)=⎩ ⎨ ⎧(a+2)∣d∣3−(a+3)∣d∣2+1a∣d∣3−5a∣d∣2+8a∣d∣−4a0 for ∣d∣≤1 for 1<∣d∣<2 otherwise
其中 a a a通常为-0.5或-1, d d d为16个点到 ( x , y ) (x,y) (x,y)沿 X X X或 Y Y Y轴的距离。双三次插值通过以下公式进行计算:
G ( x ^ , y ^ ) = ∑ m = 0 3 ∑ n = 0 3 W ( x m ) ⋅ W ( y n ) ⋅ O ( x m , y n ) G(\hat{x}, \hat{y})=\sum_{m=0}^{3} \sum_{n=0}^{3} W\left(x_{m}\right) \cdot W\left(y_{n}\right) \cdot O\left(x_{m}, y_{n}\right) G(x^,y^)=m=0∑3n=0∑3W(xm)⋅W(yn)⋅O(xm,yn)
import cv2 as cv
import matplotlib.pyplot as plt
img = plt.imread('***.jpg')
img_down = cv.resize(img, None, fx=0.2, fy=0.2, interpolation=cv.INTER_NEAREST)
img_up1 = cv.resize(img, None, fx=10, fy=10, interpolation=cv.INTER_NEAREST) # 最近邻插值
img_up2 = cv.resize(img, None, fx=10, fy=10, interpolation=cv.INTER_LINEAR) # 双线性插值
img_up3 = cv.resize(img, None, fx=10, fy=10, interpolation=cv.INTER_CUBIC) # 双三次插值
cv.imwrite('dowm5x.jpg', img_down)
cv.imwrite('INTER_NEAREST10x.jpg', img_up1)
cv.imwrite('INTER_LINEAR10x.jpg', img_up2)
cv.imwrite('INTER_CUBIC10x.jpg', img_up3)