题目
根据一棵树的中序遍历与后序遍历构造二叉树。
注意: 你可以假设树中没有重复的元素。
例如,给出
- 中序遍历 inorder = [9,3,15,20,7]
- 后序遍历 postorder = [9,15,7,20,3] 返回如下的二叉树:

思路
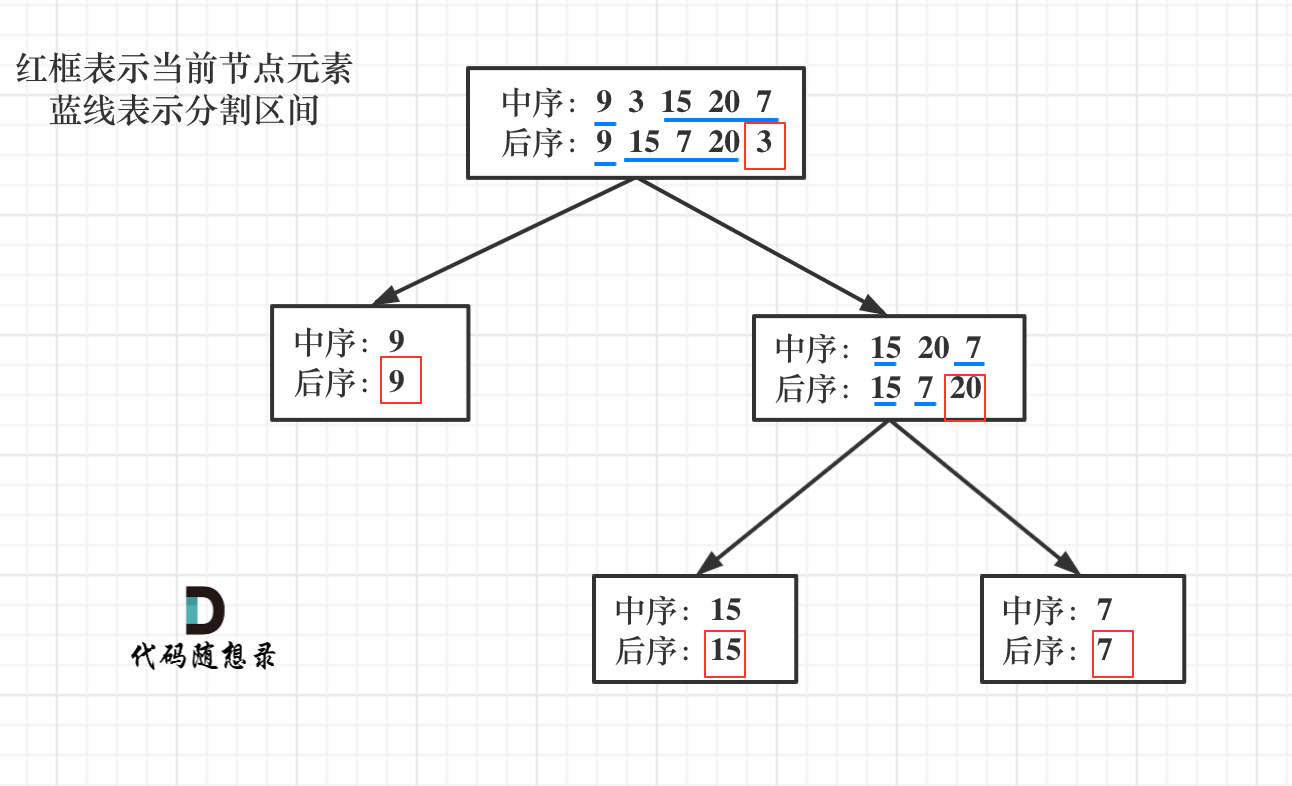
首先回忆一下如何根据两个顺序构造一个唯一的二叉树,相信理论知识大家应该都清楚,就是以 后序数组的最后一个元素为切割点,先切中序数组,根据中序数组,反过来再切后序数组。一层一层切下去,每次后序数组最后一个元素就是节点元素。
如果让我们肉眼看两个序列,画一棵二叉树的话,应该分分钟都可以画出来。
流程如图:
那么代码应该怎么写呢?
说到一层一层切割,就应该想到了递归。
来看一下一共分几步:
第一步:如果数组大小为零的话,说明是空节点了。
第二步:如果不为空,那么取后序数组最后一个元素作为节点元素。
第三步:找到后序数组最后一个元素在中序数组的位置,作为切割点
第四步:切割中序数组,切成中序左数组和中序右数组 (顺序别搞反了,一定是先切中序数组)
第五步:切割后序数组,切成后序左数组和后序右数组
第六步:递归处理左区间和右区间
不难写出如下代码:(先把框架写出来)
TreeNode* traversal (vector<int>& inorder, vector<int>& postorder) {
// 第一步
if (postorder.size() == 0) return NULL;
// 第二步:后序遍历数组最后一个元素,就是当前的中间节点
int rootValue = postorder[postorder.size() - 1];
TreeNode* root = new TreeNode(rootValue);
// 叶子节点
if (postorder.size() == 1) return root;
// 第三步:找切割点
int delimiterIndex;
for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
if (inorder[delimiterIndex] == rootValue) break;
}
// 第四步:切割中序数组,得到 中序左数组和中序右数组
// 第五步:切割后序数组,得到 后序左数组和后序右数组
// 第六步
root->left = traversal(中序左数组, 后序左数组);
root->right = traversal(中序右数组, 后序右数组);
return root;
}
难点大家应该发现了,就是如何切割,以及边界值找不好很容易乱套。
此时应该注意确定切割的标准,是左闭右开,还有左开右闭,还是左闭右闭,这个就是不变量,要在递归中保持这个不变量。
在切割的过程中会产生四个区间,把握不好不变量的话,一会左闭右开,一会左闭右闭,必然乱套!
在刚开始的几篇关于数组和二分法的博客中都强调过循环不变量的重要性,在二分查找以及螺旋矩阵的求解中,坚持循环不变量非常重要,本题也是。
首先要切割中序数组,为什么先切割中序数组呢?
切割点在后序数组的最后一个元素,就是用这个元素来切割中序数组的,所以必要先切割中序数组。
中序数组相对比较好切,找到切割点(后序数组的最后一个元素)在中序数组的位置,然后切割,如下代码中我坚持左闭右开的原则:
// 找到中序遍历的切割点
int delimiterIndex;
for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
if (inorder[delimiterIndex] == rootValue) break;
}
// 左闭右开区间:[0, delimiterIndex)
vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
// [delimiterIndex + 1, end)
vector<int> rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end() );
接下来就要切割后序数组了。
首先后序数组的最后一个元素指定不能要了,这是切割点 也是 当前二叉树中间节点的元素,已经用了。
后序数组的切割点怎么找?
后序数组没有明确的切割元素来进行左右切割,不像中序数组有明确的切割点,切割点左右分开就可以了。
此时有一个很重的点,就是中序数组大小一定是和后序数组的大小相同的(这是必然)。
中序数组我们都切成了左中序数组和右中序数组了,那么后序数组就可以按照左中序数组的大小来切割,切成左后序数组和右后序数组。
代码如下:
// postorder 舍弃末尾元素,因为这个元素就是中间节点,已经用过了
postorder.resize(postorder.size() - 1);
// 左闭右开,注意这里使用了左中序数组大小作为切割点:[0, leftInorder.size)
vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
// [leftInorder.size(), end)
vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());
此时,中序数组切成了左中序数组和右中序数组,后序数组切割成左后序数组和右后序数组。
接下来可以递归了,代码如下:
root->left = traversal(leftInorder, leftPostorder);
root->right = traversal(rightInorder, rightPostorder);
完整代码如下:
class Solution {
private:
TreeNode* traversal (vector<int>& inorder, vector<int>& postorder) {
if (postorder.size() == 0) return NULL;
// 后序遍历数组最后一个元素,就是当前的中间节点
int rootValue = postorder[postorder.size() - 1];
TreeNode* root = new TreeNode(rootValue);
// 叶子节点
if (postorder.size() == 1) return root;
// 找到中序遍历的切割点
int delimiterIndex;
for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
if (inorder[delimiterIndex] == rootValue) break;
}
// 切割中序数组
// 左闭右开区间:[0, delimiterIndex)
vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
// [delimiterIndex + 1, end)
vector<int> rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end() );
// postorder 舍弃末尾元素
postorder.resize(postorder.size() - 1);
// 切割后序数组
// 依然左闭右开,注意这里使用了左中序数组大小作为切割点
// [0, leftInorder.size)
vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
// [leftInorder.size(), end)
vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());
root->left = traversal(leftInorder, leftPostorder);
root->right = traversal(rightInorder, rightPostorder);
return root;
}
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
if (inorder.size() == 0 || postorder.size() == 0) return NULL;
return traversal(inorder, postorder);
}
};
相信大家自己就算是思路清晰, 代码写出来一定是各种问题,所以一定要加日志来调试,看看是不是按照自己思路来切割的,不要大脑模拟,那样越想越糊涂。
加了日志的代码如下:(加了日志的代码不要在leetcode上提交,容易超时)
class Solution {
private:
TreeNode* traversal (vector<int>& inorder, vector<int>& postorder) {
if (postorder.size() == 0) return NULL;
int rootValue = postorder[postorder.size() - 1];
TreeNode* root = new TreeNode(rootValue);
if (postorder.size() == 1) return root;
int delimiterIndex;
for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
if (inorder[delimiterIndex] == rootValue) break;
}
vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
vector<int> rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end() );
postorder.resize(postorder.size() - 1);
vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());
// 以下为日志
cout << "----------" << endl;
cout << "leftInorder :";
for (int i : leftInorder) {
cout << i << " ";
}
cout << endl;
cout << "rightInorder :";
for (int i : rightInorder) {
cout << i << " ";
}
cout << endl;
cout << "leftPostorder :";
for (int i : leftPostorder) {
cout << i << " ";
}
cout << endl;
cout << "rightPostorder :";
for (int i : rightPostorder) {
cout << i << " ";
}
cout << endl;
root->left = traversal(leftInorder, leftPostorder);
root->right = traversal(rightInorder, rightPostorder);
return root;
}
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
if (inorder.size() == 0 || postorder.size() == 0) return NULL;
return traversal(inorder, postorder);
}
};
此时应该发现了,如上的代码性能并不好,因为每层递归定义了新的vector(就是数组),既耗时又耗空间,但上面的代码是最好理解的,为了方便读者理解,所以用如上的代码来讲解。
下面给出用下标索引写出的代码版本:(思路是一样的,只不过不用重复定义vector了,每次用下标索引来分割)
class Solution {
private:
// 中序区间:[inorderBegin, inorderEnd),后序区间[postorderBegin, postorderEnd)
TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& postorder, int postorderBegin, int postorderEnd) {
if (postorderBegin == postorderEnd) return NULL;
int rootValue = postorder[postorderEnd - 1];
TreeNode* root = new TreeNode(rootValue);
if (postorderEnd - postorderBegin == 1) return root;
int delimiterIndex;
for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
if (inorder[delimiterIndex] == rootValue) break;
}
// 切割中序数组
// 左中序区间,左闭右开[leftInorderBegin, leftInorderEnd)
int leftInorderBegin = inorderBegin;
int leftInorderEnd = delimiterIndex;
// 右中序区间,左闭右开[rightInorderBegin, rightInorderEnd)
int rightInorderBegin = delimiterIndex + 1;
int rightInorderEnd = inorderEnd;
// 切割后序数组
// 左后序区间,左闭右开[leftPostorderBegin, leftPostorderEnd)
int leftPostorderBegin = postorderBegin;
int leftPostorderEnd = postorderBegin + delimiterIndex - inorderBegin; // 终止位置是 需要加上 中序区间的大小size
// 右后序区间,左闭右开[rightPostorderBegin, rightPostorderEnd)
int rightPostorderBegin = postorderBegin + (delimiterIndex - inorderBegin);
int rightPostorderEnd = postorderEnd - 1; // 排除最后一个元素,已经作为节点了
root->left = traversal(inorder, leftInorderBegin, leftInorderEnd, postorder, leftPostorderBegin, leftPostorderEnd);
root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, postorder, rightPostorderBegin, rightPostorderEnd);
return root;
}
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
if (inorder.size() == 0 || postorder.size() == 0) return NULL;
// 左闭右开的原则
return traversal(inorder, 0, inorder.size(), postorder, 0, postorder.size());
}
};
那么这个版本写出来依然要打日志进行调试,打日志的版本如下:(该版本不要在leetcode上提交,容易超时)
class Solution {
private:
TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& postorder, int postorderBegin, int postorderEnd) {
if (postorderBegin == postorderEnd) return NULL;
int rootValue = postorder[postorderEnd - 1];
TreeNode* root = new TreeNode(rootValue);
if (postorderEnd - postorderBegin == 1) return root;
int delimiterIndex;
for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
if (inorder[delimiterIndex] == rootValue) break;
}
// 切割中序数组
// 左中序区间,左闭右开[leftInorderBegin, leftInorderEnd)
int leftInorderBegin = inorderBegin;
int leftInorderEnd = delimiterIndex;
// 右中序区间,左闭右开[rightInorderBegin, rightInorderEnd)
int rightInorderBegin = delimiterIndex + 1;
int rightInorderEnd = inorderEnd;
// 切割后序数组
// 左后序区间,左闭右开[leftPostorderBegin, leftPostorderEnd)
int leftPostorderBegin = postorderBegin;
int leftPostorderEnd = postorderBegin + delimiterIndex - inorderBegin; // 终止位置是 需要加上 中序区间的大小size
// 右后序区间,左闭右开[rightPostorderBegin, rightPostorderEnd)
int rightPostorderBegin = postorderBegin + (delimiterIndex - inorderBegin);
int rightPostorderEnd = postorderEnd - 1; // 排除最后一个元素,已经作为节点了
cout << "----------" << endl;
cout << "leftInorder :";
for (int i = leftInorderBegin; i < leftInorderEnd; i++) {
cout << inorder[i] << " ";
}
cout << endl;
cout << "rightInorder :";
for (int i = rightInorderBegin; i < rightInorderEnd; i++) {
cout << inorder[i] << " ";
}
cout << endl;
cout << "leftpostorder :";
for (int i = leftPostorderBegin; i < leftPostorderEnd; i++) {
cout << postorder[i] << " ";
}
cout << endl;
cout << "rightpostorder :";
for (int i = rightPostorderBegin; i < rightPostorderEnd; i++) {
cout << postorder[i] << " ";
}
cout << endl;
root->left = traversal(inorder, leftInorderBegin, leftInorderEnd, postorder, leftPostorderBegin, leftPostorderEnd);
root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, postorder, rightPostorderBegin, rightPostorderEnd);
return root;
}
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
if (inorder.size() == 0 || postorder.size() == 0) return NULL;
return traversal(inorder, 0, inorder.size(), postorder, 0, postorder.size());
}
};
相关题目推荐
从前序与中序遍历序列构造二叉树
根据一棵树的前序遍历与中序遍历构造二叉树。
注意: 你可以假设树中没有重复的元素。
例如,给出
前序遍历 preorder = [3,9,20,15,7] 中序遍历 inorder = [9,3,15,20,7] 返回如下的二叉树:

思路
和上一个题目是一样的道理。下面直接给出代码。
带日志的版本C++代码如下: (带日志的版本仅用于调试,不要在leetcode上提交,会超时)
class Solution {
private:
TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& preorder, int preorderBegin, int preorderEnd) {
if (preorderBegin == preorderEnd) return NULL;
int rootValue = preorder[preorderBegin]; // 注意用preorderBegin 不要用0
TreeNode* root = new TreeNode(rootValue);
if (preorderEnd - preorderBegin == 1) return root;
int delimiterIndex;
for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
if (inorder[delimiterIndex] == rootValue) break;
}
// 切割中序数组
// 中序左区间,左闭右开[leftInorderBegin, leftInorderEnd)
int leftInorderBegin = inorderBegin;
int leftInorderEnd = delimiterIndex;
// 中序右区间,左闭右开[rightInorderBegin, rightInorderEnd)
int rightInorderBegin = delimiterIndex + 1;
int rightInorderEnd = inorderEnd;
// 切割前序数组
// 前序左区间,左闭右开[leftPreorderBegin, leftPreorderEnd)
int leftPreorderBegin = preorderBegin + 1;
int leftPreorderEnd = preorderBegin + 1 + delimiterIndex - inorderBegin; // 终止位置是起始位置加上中序左区间的大小size
// 前序右区间, 左闭右开[rightPreorderBegin, rightPreorderEnd)
int rightPreorderBegin = preorderBegin + 1 + (delimiterIndex - inorderBegin);
int rightPreorderEnd = preorderEnd;
cout << "----------" << endl;
cout << "leftInorder :";
for (int i = leftInorderBegin; i < leftInorderEnd; i++) {
cout << inorder[i] << " ";
}
cout << endl;
cout << "rightInorder :";
for (int i = rightInorderBegin; i < rightInorderEnd; i++) {
cout << inorder[i] << " ";
}
cout << endl;
cout << "leftPreorder :";
for (int i = leftPreorderBegin; i < leftPreorderEnd; i++) {
cout << preorder[i] << " ";
}
cout << endl;
cout << "rightPreorder :";
for (int i = rightPreorderBegin; i < rightPreorderEnd; i++) {
cout << preorder[i] << " ";
}
cout << endl;
root->left = traversal(inorder, leftInorderBegin, leftInorderEnd, preorder, leftPreorderBegin, leftPreorderEnd);
root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, preorder, rightPreorderBegin, rightPreorderEnd);
return root;
}
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
if (inorder.size() == 0 || preorder.size() == 0) return NULL;
return traversal(inorder, 0, inorder.size(), preorder, 0, preorder.size());
}
};
无日志的最后版本,C++代码:
class Solution {
private:
TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& preorder, int preorderBegin, int preorderEnd) {
if (preorderBegin == preorderEnd) return NULL;
int rootValue = preorder[preorderBegin]; // 注意用preorderBegin 不要用0
TreeNode* root = new TreeNode(rootValue);
if (preorderEnd - preorderBegin == 1) return root;
int delimiterIndex;
for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
if (inorder[delimiterIndex] == rootValue) break;
}
// 切割中序数组
// 中序左区间,左闭右开[leftInorderBegin, leftInorderEnd)
int leftInorderBegin = inorderBegin;
int leftInorderEnd = delimiterIndex;
// 中序右区间,左闭右开[rightInorderBegin, rightInorderEnd)
int rightInorderBegin = delimiterIndex + 1;
int rightInorderEnd = inorderEnd;
// 切割前序数组
// 前序左区间,左闭右开[leftPreorderBegin, leftPreorderEnd)
int leftPreorderBegin = preorderBegin + 1;
int leftPreorderEnd = preorderBegin + 1 + delimiterIndex - inorderBegin; // 终止位置是起始位置加上中序左区间的大小size
// 前序右区间, 左闭右开[rightPreorderBegin, rightPreorderEnd)
int rightPreorderBegin = preorderBegin + 1 + (delimiterIndex - inorderBegin);
int rightPreorderEnd = preorderEnd;
root->left = traversal(inorder, leftInorderBegin, leftInorderEnd, preorder, leftPreorderBegin, leftPreorderEnd);
root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, preorder, rightPreorderBegin, rightPreorderEnd);
return root;
}
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
if (inorder.size() == 0 || preorder.size() == 0) return NULL;
// 参数坚持左闭右开的原则
return traversal(inorder, 0, inorder.size(), preorder, 0, preorder.size());
}
};
思考
前序和中序可以唯一确定一棵二叉树。
后序和中序可以唯一确定一棵二叉树。
那么前序和后序可不可以唯一确定一棵二叉树呢?
前序和后序不能唯一确定一棵二叉树!,因为没有中序遍历无法确定左右部分,也就是无法分割。
举一个例子:
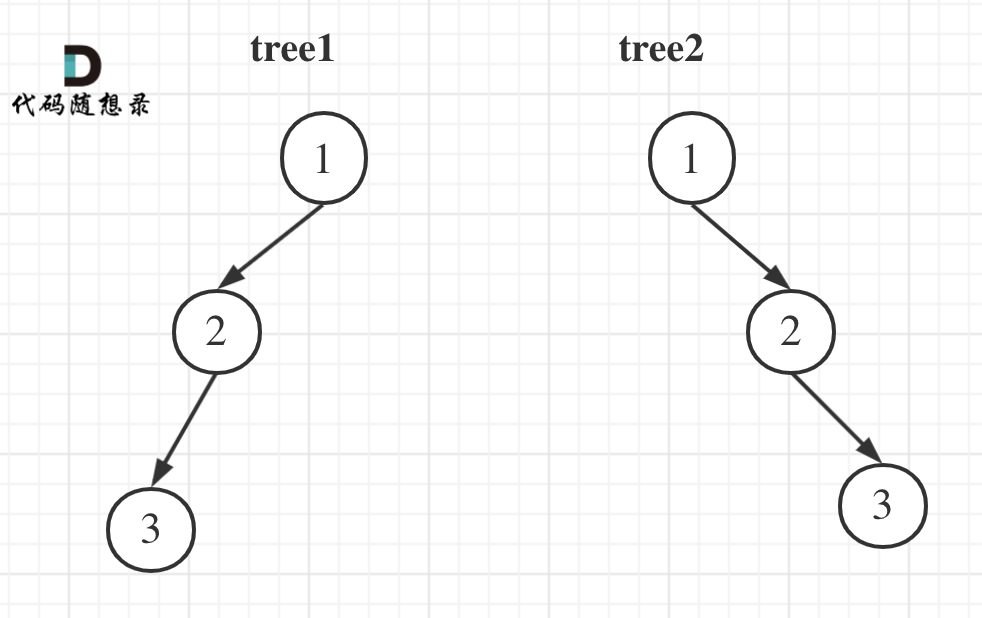
tree1 的前序遍历是[1 2 3], 后序遍历是[3 2 1]。
tree2 的前序遍历是[1 2 3], 后序遍历是[3 2 1]。
那么tree1 和 tree2 的前序和后序完全相同,这是一棵树么,很明显是两棵树!
所以前序和后序不能唯一确定一棵二叉树!