比赛链接
毕竟是娱乐场,放平心态打吧。。。
只有A一个考了数学期望,其他的基本都是acmer特有的脑筋急转弯,看个乐呵即可。
A 我是欧皇,赚到盆满钵满!
思路:
我们有 p 1 p_1 p1 的概率直接拿到一件实物,有 1 − p 1 1-p_1 1−p1 的概率拿到 10 10 10 牛币,然后去第二个抽奖。第二个是 p 2 p_2 p2 的概率拿到一件实物, p 3 p_3 p3 的概率重新抽卡, 剩下的概率就啥也没有。另外的第三四个抽奖和前面没有关系,第三个抽到实物的概率是 p 4 p_4 p4,第四个是 1 10 \dfrac1{10} 101。
我们假设第二个抽奖拿到实物的期望为 f f f,那么有: f = p 2 ∗ 1 + p 3 ∗ f f=p_2*1+p_3*f f=p2∗1+p3∗f ( 1 − p 3 ) ∗ f = p 2 (1-p_3)*f=p_2 (1−p3)∗f=p2 f = p 2 1 − p 3 f=\dfrac{p_2}{1-p_3} f=1−p3p2我们有 1 − p 1 1-p_1 1−p1 能拿到牛币,才能去第二个抽奖,这样第一个抽奖拿到实物的期望就是 p 1 ∗ 1 + ( 1 − p 1 ) ∗ f p_1*1+(1-p_1)*f p1∗1+(1−p1)∗f p 1 + ( 1 − p 1 ) ∗ p 2 1 − p 3 p_1+\dfrac{(1-p_1)*p_2}{1-p_3} p1+1−p3(1−p1)∗p2
那么总的拿到实物的期望就是 p 1 + ( 1 − p 1 ) ∗ p 2 1 − p 3 + p 4 + 1 10 p_1+\dfrac{(1-p_1)*p_2}{1-p_3}+p_4+\dfrac1{10} p1+1−p3(1−p1)∗p2+p4+101
code:
#include <iostream>
#include <cstdio>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
ll qpow(ll a,ll b){
b%=mod-1;
ll base=a%mod,ans=1;
while(b){
if(b&1){
ans=(base*ans)%mod;
}
base=(base*base)%mod;
b>>=1;
}
return ans;
}
ll inv(ll x){return qpow(x,mod-2);}
ll a,b,c,d,e,f,g,h;
ll p1,p2,p3,p4;
int main(){
cin>>a>>b>>c>>d>>e>>f>>g>>h;
p1=a*inv(b)%mod;
p2=c*inv(d)%mod;
p3=e*inv(f)%mod;
p4=g*inv(h)%mod;
cout<<(p1+p2*(1-p1+mod)%mod*inv(1-p3+mod)%mod+p4+inv(10))%mod;
return 0;
}
B 我是欧皇,赚到盆满钵满!(fool version)
思路:
不难,也没啥坑,但是榜歪了没人写。
第一三四个抽奖只能玩一次,只能拿到有限的实物,所以我们可以直接无视。因为我们有无限的牛币,可以抽无限次,所以只要第二个抽奖有概率能拿到实物,那么就相当于可以拿到无限的实物。因此这个题只要保证 p 2 > 0 p_2>0 p2>0 就行了。
code:
#include <iostream>
#include <cstdio>
using namespace std;
typedef long long ll;
ll a,b,c,d,e,f,g,h;
int main(){
cin>>a>>b>>c>>d>>e>>f>>g>>h;
if(c!=0)cout<<"Infinity";
else cout<<"limited";
return 0;
}
C 征战沙场
思路:
不懂出题人的脑回路。
样例说明说没有队友,所以你不属于任何一方。最少要和打剩下的人打,最多要全打一遍。
code:
#include <iostream>
#include <cstdio>
using namespace std;
int x,y;
int main(){
cin>>x>>y;
cout<<abs(x-y)<<" "<<x+y;
return 0;
}
D 炼药锅
思路:
经典脑筋急转弯。
这题不是问你有几口锅,而是锅有几个口。
code:
#include <iostream>
#include <cstdio>
using namespace std;
int main(){
cout<<1;
return 0;
}
E what connection?
思路:
参考牛客题解讨论区。
这几个单词是 .io .edu .cn .one .com .org 等域名的全称。它们都是 顶级域名(top-level domain)
code:
#include <iostream>
#include <cstdio>
using namespace std;
int main(){
cout<<"top-level domain";
return 0;
}
F 逻辑大师
思路:
数学天才,逻辑大师可以手玩。我是逻辑低手,我选择爆搜。
code:
没写,愚人节满课,清明还要调休,题面看着就来气。尝试当逻辑糕手的时候还推错了(以为第三题正确答案以外的其他三个选项的答案是一致的)。
答案如下:
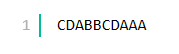
G mutsumi的……&数#¥@数
思路:
随便搜个乱码恢复的网站丢上去大概能得到这个:

mutumi有一个数组,她想知道数组里正数和负数共有几个
彩蛋我是真没找到
code:
#include <iostream>
#include <cstdio>
using namespace std;
int n,ans;
int main(){
cin>>n;
for(int i=1,t;i<=n;i++){
cin>>t;
if(t!=0)ans++;
}
cout<<ans<<endl;
return 0;
}
H 一个简单的数学题
思路:
1e18是个浮点数,因此有可能会出现精度损失。在一个大浮点数和小浮点数相加的时候,小数可能直接舍入导致消失了。
code:
#include <iostream>
#include <cstdio>
using namespace std;
int main(){
int i;
for(i=1;1e18+i==1e18;i++);
cout<<i-1;
return 0;
}
I 小苯的排列构造
思路:
从 1 1 1 按顺序输出到 n n n 即可。因为相邻两数一定是互质的。
证明可以利用辗转相除法。众所周知 g c d ( a , b ) = g c d ( b , a % b ) gcd(a,b)=gcd(b,a\%b) gcd(a,b)=gcd(b,a%b),当 a = b + 1 a=b+1 a=b+1(两数相邻)时,就有 g c d ( a , b ) = g c d ( b + 1 , b ) = g c d ( b , 1 ) = 1 gcd(a,b)=gcd(b+1,b)=gcd(b,1)=1 gcd(a,b)=gcd(b+1,b)=gcd(b,1)=1
code:
#include <iostream>
#include <cstdio>
using namespace std;
int T,n;
int main(){
cin>>T;
while(T--){
cin>>n;
for(int i=1;i<=n;i++)cout<<i<<" \n"[i==n];
}
return 0;
}
J ✌
思路:
https://t.bilibili.com/762931495002177560
都给我去看兰子哥哥的女装!
网址中很容易看出来和bilibili有关,还要和牛客有关,从牛客B站官方动态一路往下翻就翻到了。
code:
#include <iostream>
#include <cstdio>
using namespace std;
int main(){
cout<<"https://t.bilibili.com/762931495002177560";
return 0;
}
K white-collar teacher 说唱歌手 me
思路:
看评论区题解:
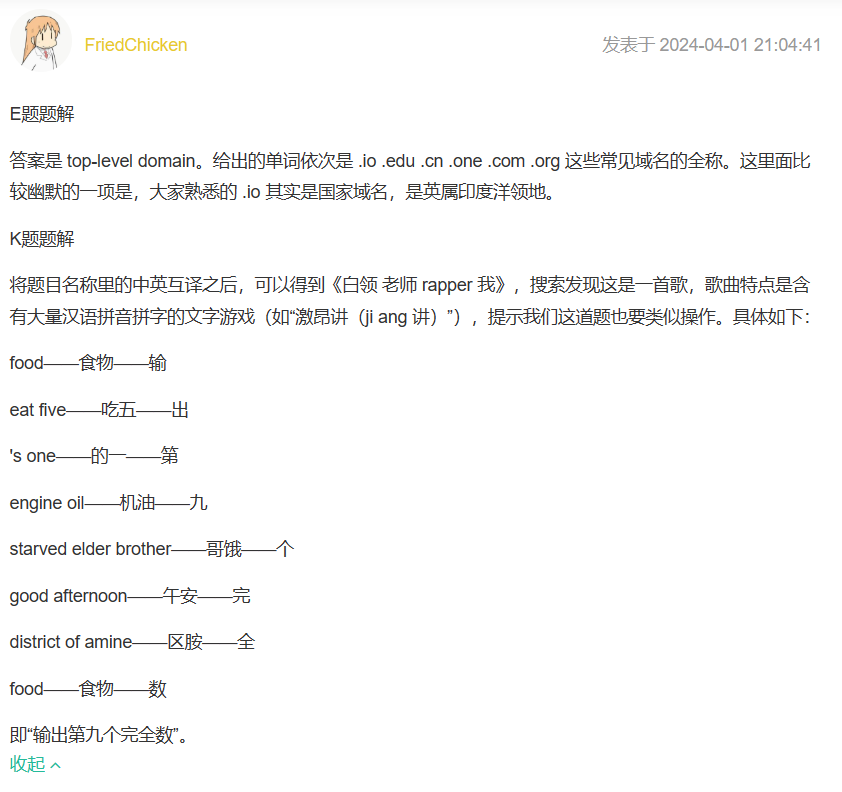
完全数的定义:

直接搜可以得到第九个完全数。
6,28,496,8128,33550336,8589869056,137438691328,2305843008139952128,2658455991569831744654692615953842176,191561942608236107294793378084303638130997321548169216,13164036458569648337239753460458722910223472318386943117783728128,14474011154664524427946373126085988481573677491474835889066354349131199152128
code:
#include <iostream>
#include <cstdio>
using namespace std;
int main(){
cout<<"2658455991569831744654692615953842176"<<endl;
return 0;
}