一、39. 组合总和
题目链接/文章讲解/视频讲解: https://programmercarl.com/0039.%E7%BB%84%E5%90%88%E6%80%BB%E5%92%8C.html状态:已解决
1.思路
这道题跟216. 组合总和 III - 力扣(LeetCode)题思路差不多,区别在于216题要求每种组合的大小必须为k,并且一个数字最多只能使用一次。而这道题组合大小可以随意,同一个数字也可以用多次。因此,根据这两个条件我们只需要在256题的基础上去掉终止条件path.size()==k,且for循环的开始值可以从前一个递归的for循环开始值开始(不能从0到candidate.size()-1,否则会导致{2,3}和{3,2}这种看似序列不同但是是一个组合的情况)。
明确大致做法后,套用公式:
(1)确定返回值和参数:每个组合和所有组合的集合定义在回溯函数的外部,故不做参数,同时此题也不需要根据子函数的结果更新父函数的值,故无返回值。参数需要原数组candidates、下一层函数for循环的开始位置、目前的总和sum、以及目标值target。
void backtracking(vector<int>& candidates,int startIndex,int sum,int target)(2)确定终止条件:当sum>target时,再回溯下去sum的值也只会越来越大,故此时可以终止(剪枝)。还有一种终止情况就是sum==target,此时得到我们所需值,并且终止本轮回溯。
if(sum>target){
return ;
}
if(sum == target){
result.push_back(path);
return ;
}(3)回溯遍历过程:进行for循环,内部做回溯(显式path的回溯和隐式sum的回溯)
for(int i=startIndex;i<candidates.size();i++){
path.push_back(candidates[i]);
backtracking(candidates,i,sum+candidates[i],target);
path.pop_back();
}2.完整代码
class Solution {
public:
vector<int> path;
vector<vector<int>> result;
void backtracking(vector<int>& candidates,int startIndex,int sum,int target){
if(sum>target){
return ;
}
if(sum == target){
result.push_back(path);
return ;
}
for(int i=startIndex;i<candidates.size();i++){
path.push_back(candidates[i]);
backtracking(candidates,i,sum+candidates[i],target);
path.pop_back();
}
}
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
path.clear();
result.clear();
backtracking(candidates,0,0,target);
return result;
}
};二、40.组合总和II
题目链接/文章讲解/视频讲解: https://programmercarl.com/0040.%E7%BB%84%E5%90%88%E6%80%BB%E5%92%8CII.html状态:已解决
1.思路
这道题很多人一开始的想法估计都和我一样,都是先按常规写法求出结果集,然后做一个去重操作,但是大家发现这样特别麻烦!!!
这道题比39题难的点在于候选集有重复元素但是结果集中不同有重复的组合。以前我们实现去重是根据下一层递归for循环起始值大于上一层递归for循环的起始值实现的,但是由于有相同值的元素,这样的方法就不行了,如:{1,1,5,1,1,3},target=7,对于前三个元素,可以构成一个组合,对于第三到第五个元素,也可以构成一个组合,但二者实际是一样的组合,即使采用之前的方法也不管用。
卡哥在这道题引入了一个新的去重思路:自创了树层去重和树枝去重的概念。
(1)数层去重:引起重复的根本原因是因为相同值的元素出现在多个位置,而实际上如果出现在后面的重复值,其得到的有效组合必定跟曾出现在前面位置的相同元素的有效组合一致。假设我们设前面某个元素为x,后面某个元素为y,其中,x=y且y出现在x的后方。那么,如果存在{y,m,n}满足和等于target,则{x,m,n}也必定和等于target。反之,不一定成立(由下一层递归for循环起始值大于上一层递归for循环的起始值决定)。因此,其实我们只需要统计等于某个值的所有元素中,最靠前的元素的有效组合即可,其余重复值不再对其进行操作。
如何实现这个操作:先对candidates进行排序,在for循环中,如果某层循环满足candidates[i]==candidates[i-1]时,跳过,不做后面的回溯操作即可。
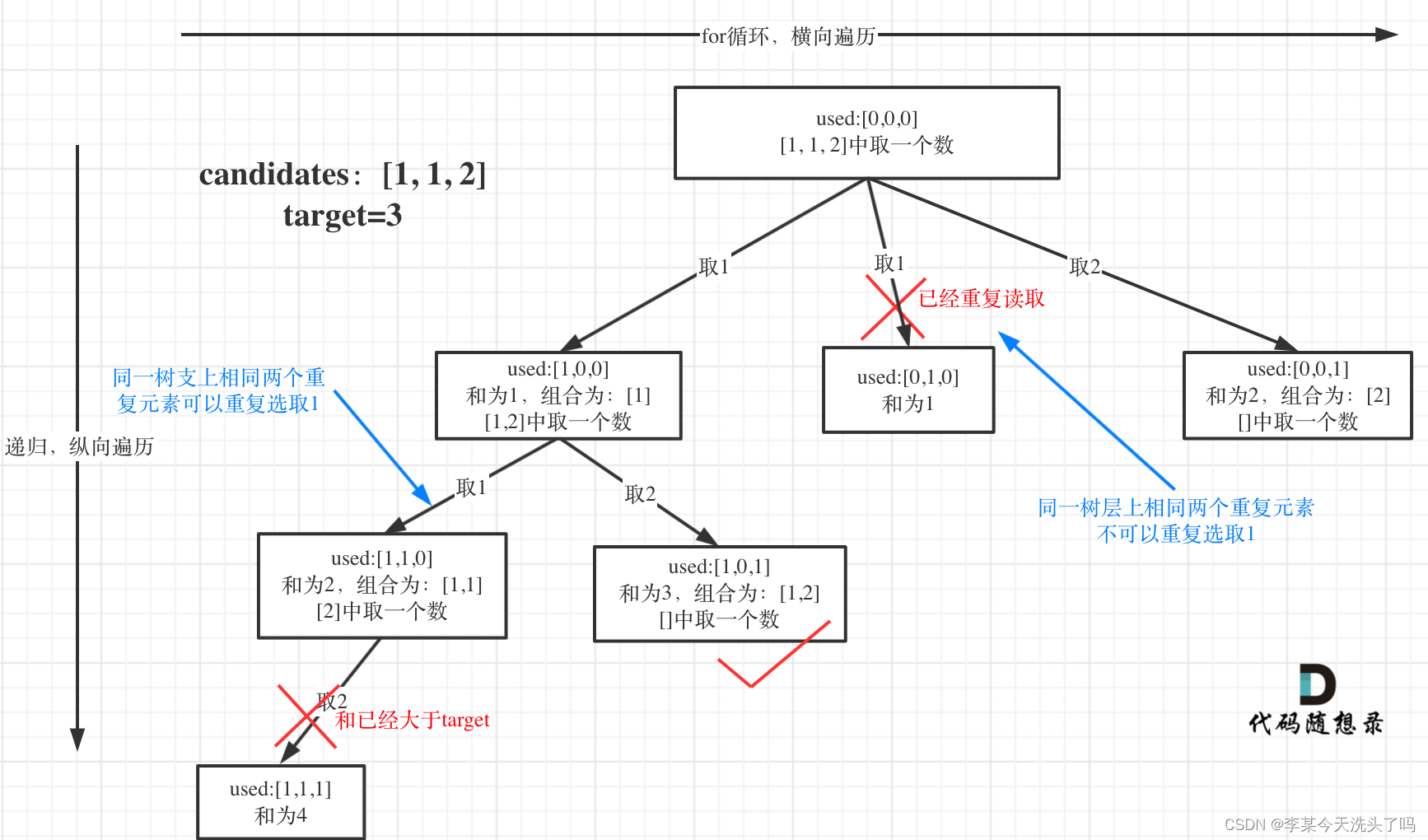
(2)树枝去重:为什么要树枝去重?因为假如candidates={1,1,2,5},target=7,现在以第一个1为开头做回溯,由于要进行树层去重,需要判断candidates[i]是否等于candidates[i-1],而第一个1和第二个1相等,故明明可以选择第二个1的时候把第二个1跳过了,导致丧失了{1,1,5}这个有效组合,因此,单单一个candidates信息是不够的,还需要其他信息。
这里卡哥采取的方法是新增一个数组used,记录哪些位置的元素被用过了。0代表未用,1代表已经使用了。如果candidates[i]已经等于candidates[i-1]了,但used[i-1]==0,则说明上一个节点未被使用,此时代表上一个元素与现在这个元素相同,但从现在这个元素开始取值,也就是说,此时是在树层位置,树层位置只对相同值中的第一个元素进行处理,故此时跳过第二个1。而假如used[i-1]==1,代表此时是以第一个1为开始元素进行回溯操作的,故代表程序进行到树枝位置,树枝位置遇到后面的重复元素是要取值的。
根据题意可总结得到关键部分代码:
if(i>0 && candidates[i]==candidates[i-1] && used[i-1]==0) continue;题目难度变大了,但是一行多余操作就能解决去重问题,甚妙!
2.完整代码
class Solution {
public:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& candidates,int target,int startIndex,int sum,vector<int>& used){
if(sum > target){
return ;
}
if(sum == target){
result.push_back(path);
return ;
}
for(int i=startIndex;i<candidates.size();i++){
if(i>0 && candidates[i]==candidates[i-1] && used[i-1]==0) continue;
path.push_back(candidates[i]);
used[i] = 1;
backtracking(candidates,target,i+1,sum+candidates[i],used);
used[i] = 0;
path.pop_back();
}
}
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
sort(candidates.begin(),candidates.end());
vector<int> used(candidates.size(),0);
backtracking(candidates,target,0,0,used);
return result;
}
};
三、131.分割回文串
题目链接/文章讲解/视频讲解: https://programmercarl.com/0131.%E5%88%86%E5%89%B2%E5%9B%9E%E6%96%87%E4%B8%B2.html状态:已解决
1.思路
我觉得这道题的关键在于如何把题意转化到回溯法上面去。其实把切割操作和组合问题的操作列出来对比一下就知道怎么转换了:
例如对于字符串abcdef:
- 组合问题:选取一个a之后,在bcdef中再去选取第二个,选取b之后在cdef中再选取第三个.....。
- 切割问题:切割一个a之后,在bcdef中再去切割第二段,切割b之后在cdef中再切割第三段.....。
实质还是一个组合问题,也就是一个回溯问题,可以画树状图来思考过程。
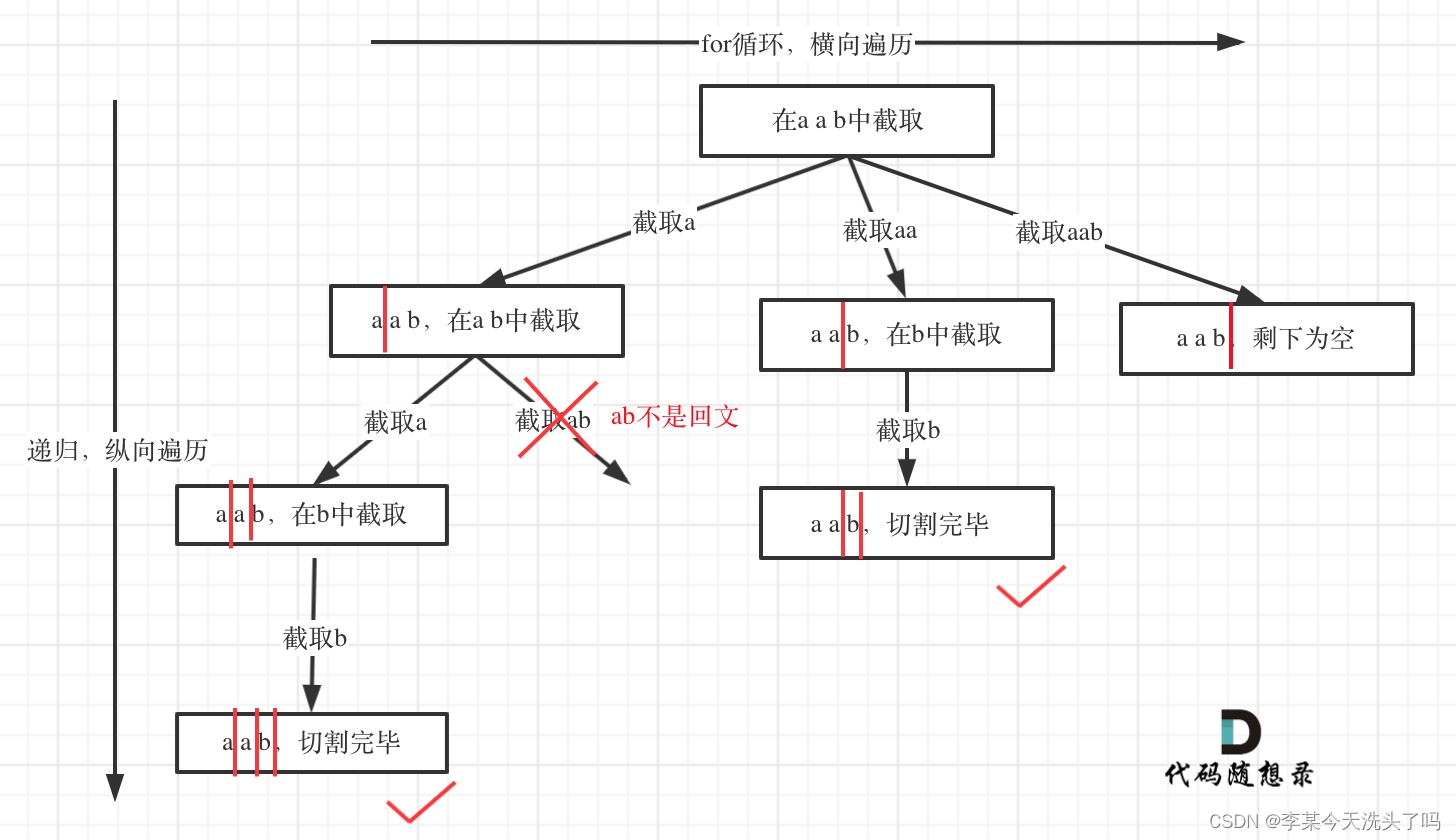
递归用于纵向遍历,而for循环用于横向遍历,那究竟如何进行切割的呢?利用startIndex,每层递归函数,在for循环中,[startIndex,i]构成的字符串就是这次操作被切割的子串,将这个子串后面的子串送入下一层递归(即startIndex=i+1)。
回溯三部曲:
(1)参数和返回值类型:返回值类型依旧为void,参数需要原字符串s,开始切割位置startIndex。
void backtracking(const string& s,int startIndex)(2)终止条件:当切割线达到字符串末尾时,切割完毕,即startIndex>=s.size() 。
if(startIndex >= s.size()){
result.push_back(path);
return;
}(3)每层递归逻辑:
for循环i从startIndex开始,向后移动,移动到一个位置, 就计算startIndex和i之间的字符串是不是回文串,是的话就将其放入path中,作为一个子串,并开始回溯,继续切割该子串后面的子串;否则,跳过该位置。
for(int i=startIndex;i<s.size();i++){
if(isPalindrome(s,startIndex,i)){
string substrs = s.substr(startIndex,i-startIndex+1);
path.push_back(substrs);
}else{
continue;
}
backtracking(s,i+1);
path.pop_back();
}2.完整代码
完整代码只需要添加一个判断回文子串的函数(用双指针法)。
class Solution {
public:
vector<string> path;
vector<vector<string>> result;
bool isPalindrome(const string& s,int startIndex,int i){
for(int left = startIndex,right = i;left < right;left++,right--){
if(s[left] != s[right]) return false;
}
return true;
}
void backtracking(const string& s,int startIndex){
if(startIndex >= s.size()){
result.push_back(path);
return;
}
for(int i=startIndex;i<s.size();i++){
if(isPalindrome(s,startIndex,i)){
string substrs = s.substr(startIndex,i-startIndex+1);
path.push_back(substrs);
}else{
continue;
}
backtracking(s,i+1);
path.pop_back();
}
}
vector<vector<string>> partition(string s) {
path.clear();
result.clear();
backtracking(s,0);
return result;
}
};