一句话总结:初看觉得难,过几天再做依旧觉得不简单。
原题链接:343 整数拆分

拿到题乍一看两眼一抹黑。还是看题解吧。首先确定动规数组及下标的含义。这里就设置dp[i]为正整数i的最大乘积。
然后确定递推关系式。对于怎么求i的最大乘积,有两种方式,从1遍历到j,那么dp[i]有两种可能的取得途径:
- j 与 (i - j)直接相乘
- j与dp[i - j],相当于是递归地计算最大值。
因此dp[i]从j * (i - j), dp[i - j] * j, 以及dp[i]三者中取最大值即可。
第三步是对dp数组地初始化,这里初始化dp[0]和dp[1]从题目的角度来看是无意义的,因为拆分0和拆分1的最大乘积无意义。故直接初始化dp[2] = 1即可。
第四步是确定遍历顺序。通过递归公式dp[i] = max(dp[i], dp[i - j] * j, (i - j) * j)可以看出来,dp[i]依赖前面计算得到的dp[i - j],因此从前往后遍历。
通过以上四步已经可以写出来完整的代码了,但为了程序的完整性,还需要一步,即举例手推一遍代码,过程不表。以下是代码:
class Solution {
public int integerBreak(int n) {
int[] dp = new int[n + 1];
dp[2] = 1;
for (int i = 3; i <= n; ++i) {
for (int j = 0; j < i - 1; ++j) {
dp[i] = Math.max(dp[i], Math.max(dp[i - j] * j, (i - j) * j));
}
}
return dp[n];
}
}然后此题还有一种巧妙的数学解法,通过数学推导可得出在将该整数尽可能多的拆分出3以后即可使得答案最大。原题解在此。
class Solution {
public int integerBreak(int n) {
if (n < 4) return n - 1;
int a = n / 3, b = n % 3;
if (b == 0) return (int) Math.pow(3, a);
if (b == 1) return (int) Math.pow(3, a - 1) * 4;
return (int) Math.pow(3, a) * 2;
}
}原题链接:96 不同的二叉搜索树
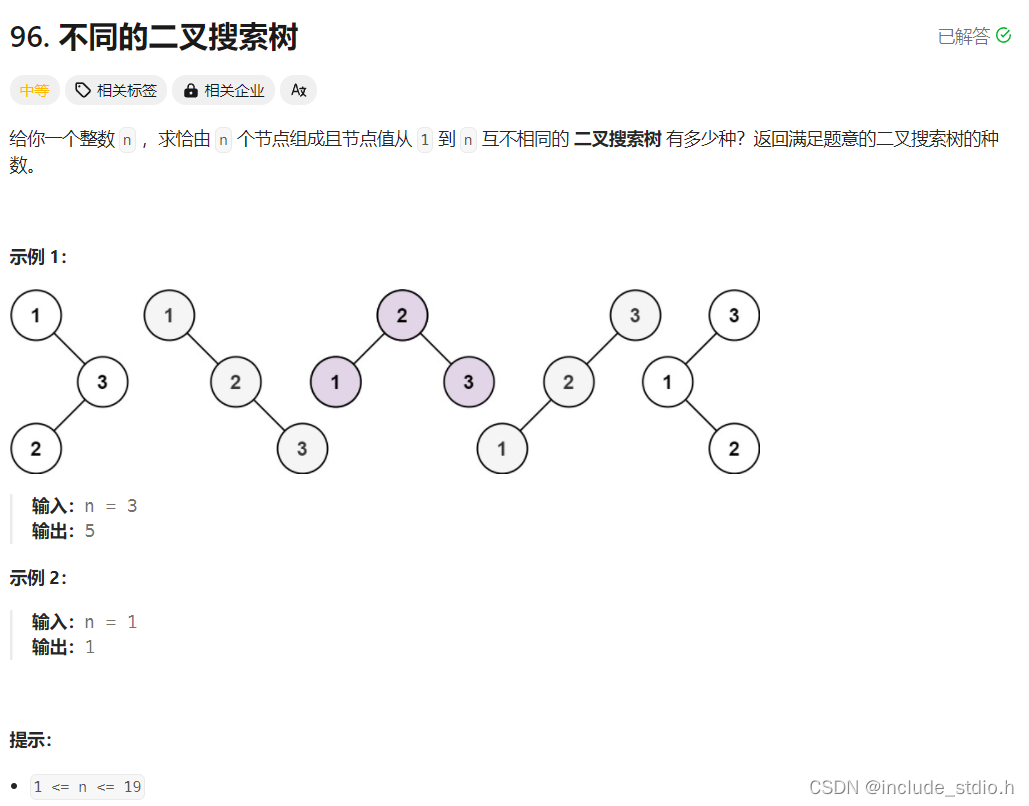
按照动态规划的五部曲来。
首先确定dp数组及下标的含义,即dp[i]表示为i个节点可组成的不同二叉搜索树的种类。
然后确定dp数组的递归公式。这里可以思考一下,如果计算的是dp[3],即树中有三个节点,那么dp[3] = dp[以节点3为根节点的二叉搜索树的数量] + dp[以节点1为根节点的二叉搜索树的数量] + dp[以节点2为根节点的二叉搜索树的数量]。即可以更深的理解为,dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量],其中j的取值范围为1到i。
第三步是初始化这个数组。很容易想到一个节点时只有一种情况,两个节点是两种不同的树。实际上初始化dp[1] = 1即可。
第四步是确定遍历顺序,从公式来看,当前计算的i依赖于此前计算出来的i - j的dp值,因此需要从前往后遍历。
到这里已经可以写出完整的代码了,但不妨进行第五步,手写计算一下验证代码是否正确。
以下是代码。
class Solution {
public int numTrees(int n) {
int[] dp = new int[n + 1];
dp[0] = 1;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= i; ++j) {
dp[i] += dp[j - 1] * dp[i - j];
}
}
return dp[n];
}
}